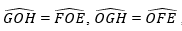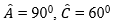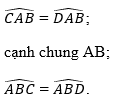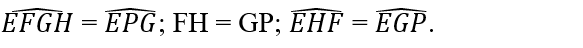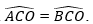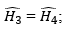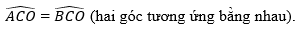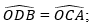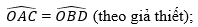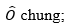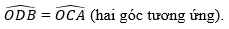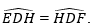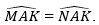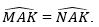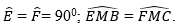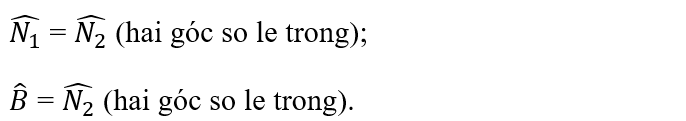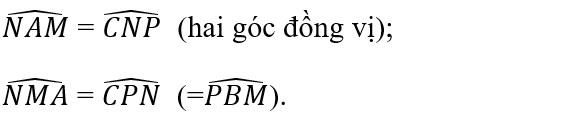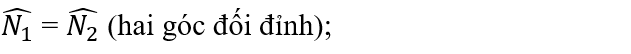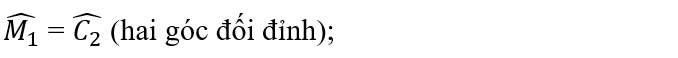Giải Toán lớp 7 VNEN Bài 4: Trường hợp bằng nhau góc-cạnh-góc

Hướng dẫn Giải bài tập Toán VNEN Bài 4: Trường hợp bằng nhau góc-cạnh-góc trang 125 đến 129 Hình học Tập 1 chương 2 sách giáo khoa lớp 7 chương trình mới chính xác, ngắn gọn và dễ hiểu dưới đây sẽ giúp các em học sinh trả lời các câu hỏi và giải các bài toán nhanh chóng, tiếp thu bài học trên lớp tốt hơn.

A. Hoạt động khởi động Bài 4: Trường hợp bằng nhau góc-cạnh-góc

Câu 1: (trang 125 SGK Toán lớp 7 VNEN tập 1 chương 2)

Thực hiện các hoạt động sau

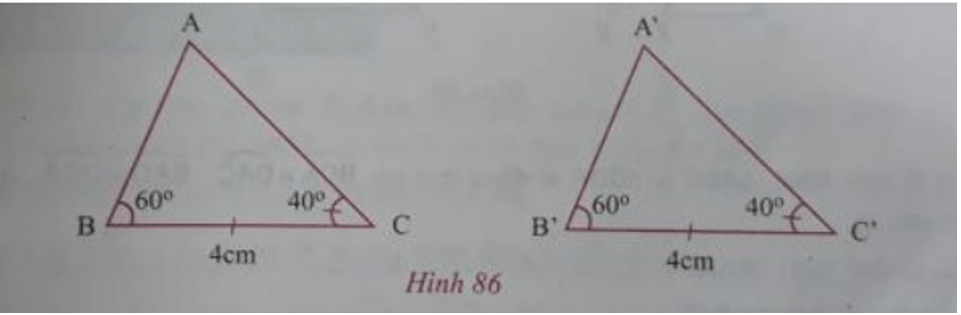
- Vẽ △ABC và △A′B′C′ vào vở, biết rằng BC = B’C’ = 4 cm;

 

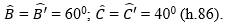
- Đo độ dài hai cạnh BA và B’A’ rồi so sánh độ dài hai cạnh đó.

- △ABC và △A′B′C′ có bằng nhau không? Vì sao?

Lời giải:

- Các em thực hiện vẽ hai tam giác ABC và A’B’C’ vào vở như hình 86.

- Sau khi dùng thước thẳng đo, ta thấy: BA = B’A’.

- △ABC và △A′B′C′ có bằng nhau theo trường hợp cạnh – góc – cạnh.

Câu 2: (trang 125 SGK Toán 7 VNEN tập 1 chương 2)

Đọc và ghi nhớ (Sgk)

B. Hoạt động hình thành kiến thức Bài 4: Trường hợp bằng nhau góc-cạnh-góc

Câu 1: (trang 126 SGK VNEN Toán lớp 7 tập 1 chương 2)

a) Đọc kĩ nội dung sau (sgk)

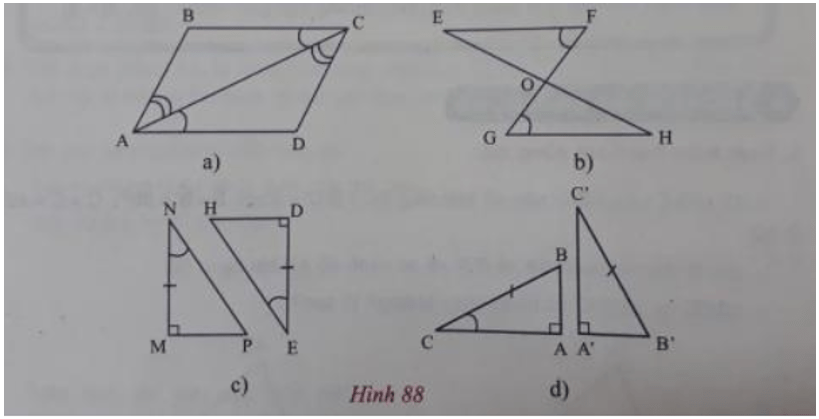
b) Em hãy quan sát các hình vẽ trên hình 88 và làm theo mẫu

i) Ở hình 88a) △ABC = △CDA vì đồng thời có: 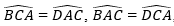 , AC là cạnh chung;

ii) Ở hình 88b), △OGH =… vì ……………..; ………………..; …………………….

iii) Ở hình 88c), △NMP =… vì ……………..; ………………..; …………………….

iv) Ở hình 88d), △A′B′C ′= … vì ……………..; ………………..; …………………….

Lời giải:

ii) Ở hình 88b), △OGH=△OFE vì đồng thời có:

iv) Ở hình 88d), △A′B′C′=△ABC vì đồng thời có: 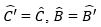 , OG = OF.

(cùng phụ với hai góc bằng nhau), B’C’ = BC.

Câu 2: (trang 127 SGK Toán VNEN lớp 7 VNEN tập 1 chương 2)

a) Qua kết quả của bài tập trên, em hãy cho biết hai tam giác vuông bằng nhau khi nào.

b) Đọc kĩ nội dung sau (skg trang 127)

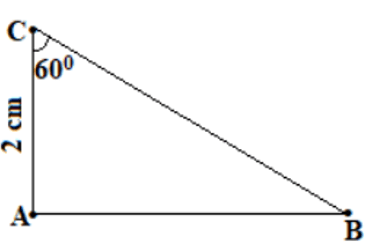
c) Bằng thước thẳng có chia đơn vị và thước đo góc hãy vẽ tam giác ABC, biết AC = 2 cm,

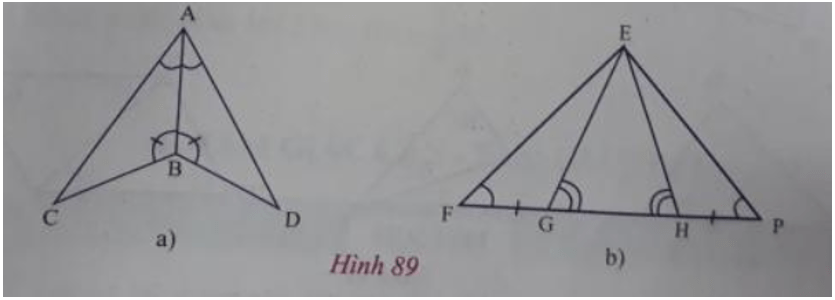
d) Trên các hình vẽ ở hình 89, có các tam giác nào bằng nhau? Vì sao?

- Ở hình 89a) △ABC = △ABD (g.c.g) vì có:

- Em hãy tự trình bày về các cặp tam giác bằng nhau có ở hình 89b) vào vở.

Lời giải:

a) Hai tam giác vuông bằng nhau khi hai tam giác đó có một cạnh góc vuông và góc kề cạnh đó bằng nhau hoặc cạnh huyền và góc nhọn bằng nhau.

c)

d)

- Ở hình 89b)

+ △FEG = △PEH (g.c.g) vì có:

+ △FEH=△PEG (g.c.g) vì có:

C. Hoạt động luyện tập Bài 4: Trường hợp bằng nhau góc-cạnh-góc

Câu 1: (trang 127 SGK Toán lớp 7 VNEN tập 1 chương 2)

Cho góc xOy khác góc bẹt, Ot là tia phân giác của góc đó. Qua điểm H thuộc tia Ot, kẻ đường vuông góc với Ot, nó cắt Ox và OY theo thứ tự ở A và B.

a) Chứng minh rằng H là trung điểm của AB.

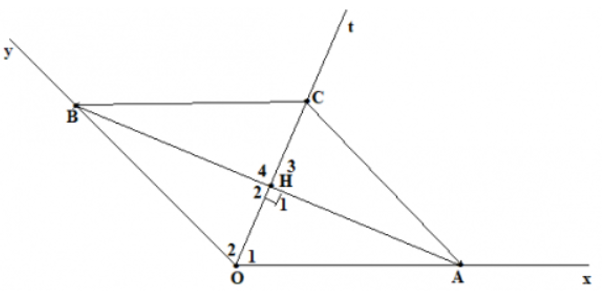
b) Lấy điểm C thuộc tia Ot, chứng minh 

Lời giải:

a) Xét △OHA và △OHB có:

OH cạnh chung;

⇒ △OHA=△OHB; (g.c.g)

Suy ra: HA = HB (hai cạnh tương ứng bằng nhau) hay H là trung điểm của AB.

b) Xét △HAC và △HBC có:

CH cạnh chung;

HA = HB (theo câu a)

⇒ △HAC=△HBC (c.g.c);

Suy ra: 

Câu 2. (trang 127 SGK Toán VNEN 7 VNEN tập 1 chương 2)

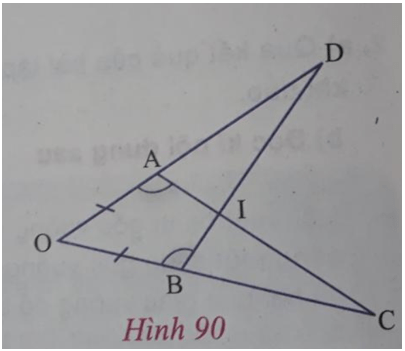
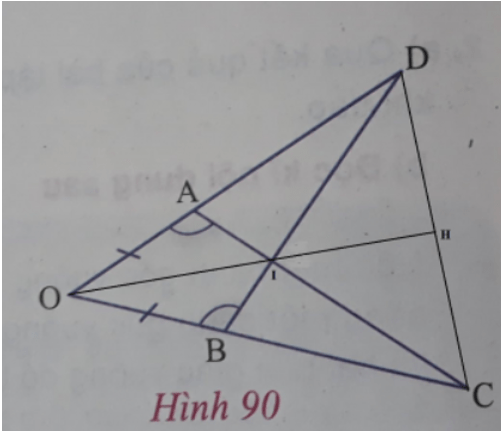
Trên hình 90, ta có OA = OB, 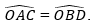 . Chứng minh:

a) 

b) ID = IC;

c) OI là tia phân giác của góc DOC và OI ⊥ CD.

Lời giải:

a) Xét △ODB và △OCA có:

OB = OA (theo giả thiết);

 

⇒ △ODB=△OCA; (g.c.g)

Suy ra:

b) Theo câu a) OD = OC (hai cạnh tương ứng) ⇒ AD = BC (hiệu của các cặp đoạn thẳng có cùng độ dài).

c)

- Chứng minh OI là tia phân giác góc DOC:

Dễ thấy △OAI=△OBI do có: OA = OB; OI chung; AI = BI ( do AI = AC – IC; IB = BD – ID mà ID = IC; AC = BD)

Suy ra:

 (hai góc tương ứng bằng nhau) hay OI là tia phân giác góc DOC.

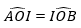
- Chứng minh: OI ⊥ CD

+ Gọi H là giao điểm của OI với CD (hình vẽ)

 

Câu 3: (trang 128 SGK VNEN Toán 7 tập 1 chương 2)

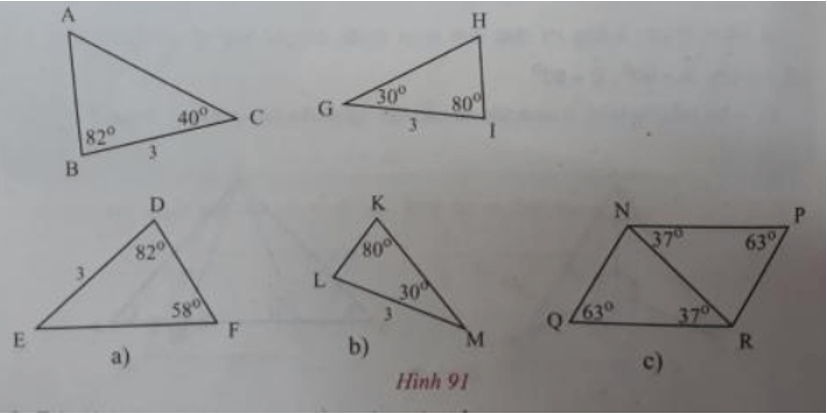
Trong các cặp tam giác dưới đây (h.91), có những cặp tam giác nào bằng nhau? Vì sao?

Lời giải:

- Ở hình 91a), △ABC và △DEF không bằng nhau vì không có các cặp cạnh tương ứng và các góc tương ứng bằng nhau.

- Ở hình 91b), △HIG và △LKM không bằng nhau vì chúng có hai góc bằng nhau nhưng cạnh xen giữa hai góc đó không bằng nhau.

- Ở hình 91c) △NPR = △RQN theo trường hợp góc – cạnh – góc.

Câu 4: (trang 128 SGK Toán lớp 7 VNEN tập 1 chương 2)

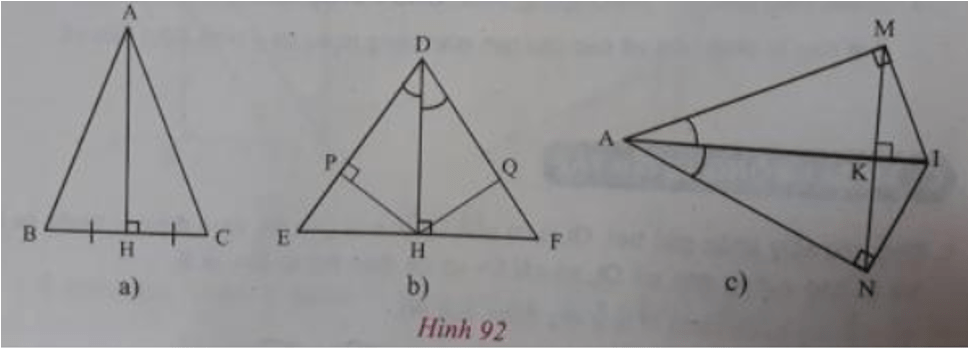
Trên hình 92 có các cặp tam giác vuông nào bằng nhau? Vì sao?

Lời giải:

- Ở hình 92a) △AHB=△AHC vì có AH chung; 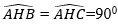 ; HB = HB.

- Ở hình 92b) △DEH=△DFH vì có DH chung; 

- Ở hình 92c:

+ △KAM=△KAN vì AK chung; 

+ △AMI=△ANI vì AI chung; 

+ △MKI=△NKI vì KI chung; 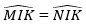 (hai góc tương ứng của hai tam giác bằng nhau: △AMI=△ANI).

Câu 5. (trang 128 SGK Toán 7 VNEN tập 1 chương 2)

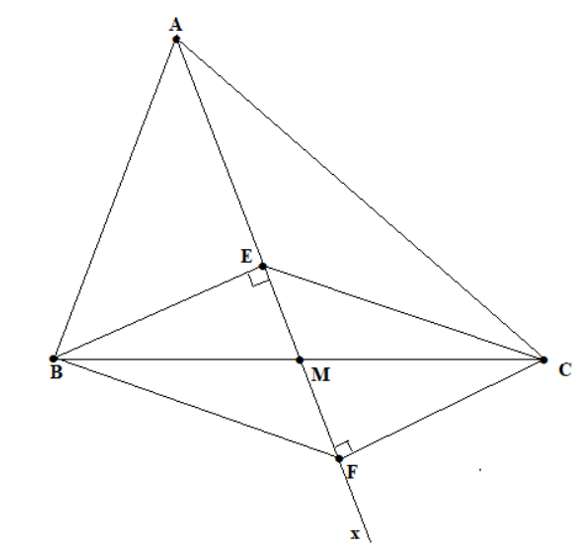
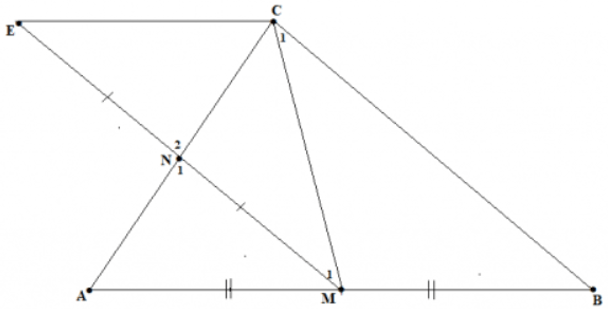
Cho tam giác ABC (AB ≠ AC), tia Ax đi qua trung điểm M của BC. Kẻ BE và CF vuông góc với Ax (E thuộc Ax, F thuộc Ax).

a) So sánh độ dài BE và CF;

b) Chứng minh rằng EC // BF.

Lời giải:

a) Dễ thấy: △BEM=△CFM vì BM = CM;

Vậy BE = CF (hai cạnh tương ứng).

b) Theo câu a,

 (hai góc tương ứng).

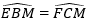
Hai đường thẳng EC và BF có hai góc ở vị trí so le trong bằng nhau nên: EC // BF.

D.E. Hoạt động vận dụng & Tìm tòi mở rộng Bài 4: Trường hợp bằng nhau góc-cạnh-góc

Câu 1: (trang 129 SGK Toán VNEN lớp 7 tập 1 chương 2)

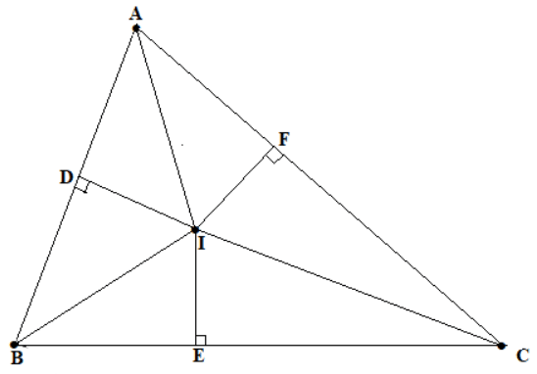
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Vẽ ID vuông góc với AB (D thuộc AB), IE vuông góc với BC (E thuộc BC), IF vuông góc với AC (F thuộc AC). Chứng minh ID = IE = IF.

Lời giải:

Xét △BDI và △BEI có:

BI chung;

⇒ △BDI=△BEI; (g.c.g)

Suy ra: ID = IE (hai cạnh tương ứng). (1)

Chứng minh tương tự: △IEC=△IFC

Suy ra: IE = IF (hai cạnh tương ứng); (2)

Từ (1) và (2): ID = IE = IF.

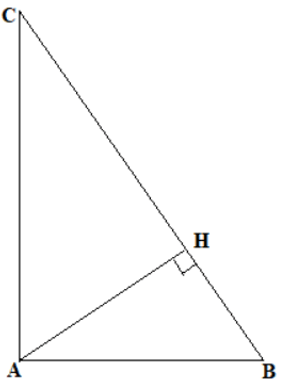
Câu 2: (trang 129 SGK VNEN Toán 7 tập 1 chương 2)

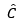
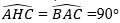
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H thuộc BC). Các tam giác AHC và BAC có AC là cạnh chung;  là góc chung, , nhưng hai tam giác đó không bằng nhau. Hãy giải thích tại sao?

Lời giải:

Hai tam giác AHC và BAC không bằng nhau vì: có hai cạnh tương ứng AH và BA không bằng nhau.

Câu 3: (trang 129 SGK Toán lớp 7 VNEN tập 1 chương 2)

Cho tam giác ABC, M là trung điểm của AB, kẻ đường thẳng qua M song song với BC cắt AC tại N. Từ N kẻ đường thẳng song song với AB cắt BC tại P. Chứng minh rằng:

a) △BMN=△NPB và AM = NP.

b) △AMN=△NPC và AN = NC.

Lời giải:

a) Xét △BMN và △NPB có:

NB chung;

⇒ △BMN=△NPB (g.c.g).

Tương tự: △ANP=△PMA (g.c.g).

Suy ra: AM = NP (hai cạnh tương ứng).

b) Xét △AMN và △NPC có:

AM = NP (theo câu a);

⇒ △AMN=△NPC (g.c.g).

Suy ra: AN = NC (hai cạnh tương ứng).

Câu 4: (trang 129 SGK Toán 7 VNEN tập 1 chương 2)

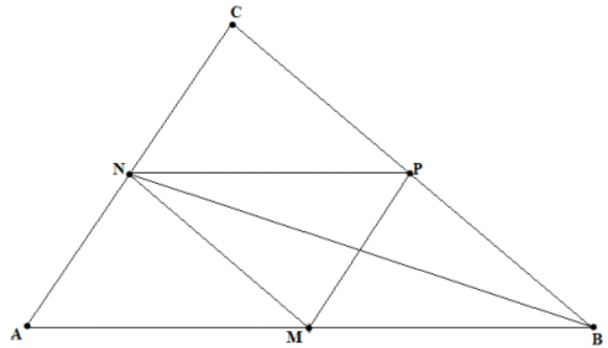
Cho tam giác ABC, M là trung điểm của AB. Từ M kẻ đường thẳng song song với BC cắt AC tại N. Lấy E trên đường thẳng MN sao cho N là trung điểm của ME. Chứng minh rằng:

a) △AMN = △CEN và CE = MB.

b) △BMC = △ECM và MN // BC; MN = 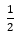BC.

Lời giải:

a) Do MN // BC mà M là trung điểm của AB nên N là trung điểm của AC (theo tính chất của đường thẳng song song).

Xét △AMN và △CEN có:

NM = NE (giả thiết);

AN = NC (chứng minh trên);

⇒ △AMN=△CEN (c.g.c) (đpcm);

⇒ AM = CE

Lại có: AM = MB (giả thiết) nên CE = BM (đpcm);

b)

- Chứng minh: △BMC=△ECM

Xét △BMC và △ECM có:

CM chung;

CE = MB (chứng minh trên);

⇒ △BMC=△ECM (c.g.c) (đpcm);

- Chứng minh: MN // BC; MN = 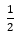BC.

+ Theo giả thiết: MN // BC (đpcm);

+ Ta có: EM = CB (hai cạnh tương ứng) mà MN = NE = 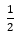 ME (theo cách vẽ);

Suy ra: MN = 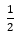 BC (đpcm)

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải Toán 7 VNEN Bài 4: Trường hợp bằng nhau góc-cạnh-góc file PDF hoàn toàn miễn phí.