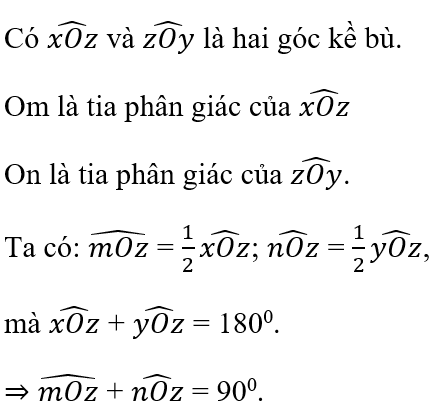Giải Toán lớp 7 VNEN Bài 5: Định Lí ngắn gọn

Hướng dẫn Giải bài tập Toán 7 VNEN Bài 5: Định Lí trang 99 đến 100 Hình học Tập 1 chương 1 sách giáo khoa lớp 7 chương trình mới chính xác, ngắn gọn và dễ hiểu dưới đây sẽ giúp các em học sinh trả lời các câu hỏi và giải các bài toán nhanh chóng, tiếp thu bài học trên lớp tốt hơn.

A. Hoạt động khởi động & Hình thành kiến thức Bài 5: Định Lí

Câu 1: (trang 99 SGK VNEN Toán lớp 7 tập 1 chương 1)

a) Trò chơi (Sgk trang 99)

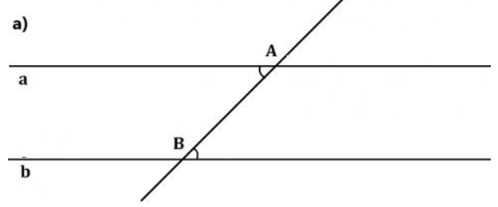
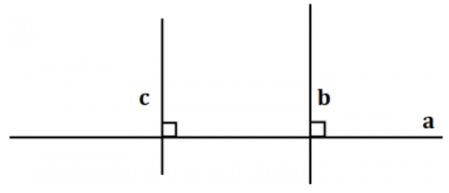
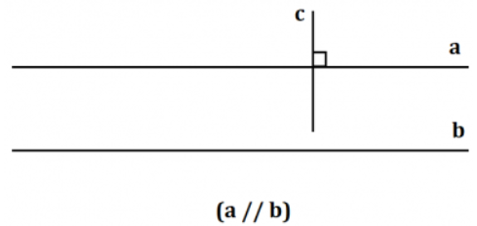
b) Xem mỗi hình vẽ ở hình 36 trong bảng sau. Phát biểu nội dung tương ứng với mỗi hình đó theo cách nói "Nếu.. thì...":

Lời giải:

Câu 2: (trang 100 SGK Toán lớp 7 VNEN tập 1 chương 1)

a) Đọc và làm theo (Sgk trang 100)

b) Đọc kĩ nội dung sau (Sgk trang 100)

c) Luyện tập

Nhớ lại trong số các kiến thức đã học xem tính chất nào có thể phát biểu thành định lí. Chỉ rõ giả thiết, kết luận với mỗi định lí được phát biểu.

Lời giải:

Một số tính chất có thể phát biểu thành định lí là:

(1) Hai đường thẳng xx' và yy' được gọi là vuông góc với nhau, kí hiệu là xx' ⊥ yy', nếu chúng cắt nhau và trong số các góc tạo thành có một góc là góc vuông.

⇒ Nếu hai đường thẳng xx' và yy' cắt nhau và trong số các góc tạo thành có một góc là góc vuông thì hai đường thẳng xx' và yy' vuông góc với nhau.

- Giả thiết là: "hai đường thẳng xx' và yy' cắt nhau và trong số các góc tạo thành có một góc là góc vuông".

- Kết luận là: "hai đường thẳng xx' và yy' vuông góc với nhau".

(2) Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại.

⇒ Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại.

- Giả thiết là: "một đường thẳng vuông góc với một trong hai đường thẳng song song".

- Kết luận là: "nó cũng vuông góc với đường thẳng còn lại".

(3) Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.

⇒ Nếu hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.

- Giả thiết là: "hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba".

- Kết luận là: "chúng song song với nhau".

C. Hoạt động luyện tập Bài 5: Định Lí

a) Cho định lí: Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông.

- Hãy cho biết giả thiết của định lí.

- Hãy cho biết kết luận của định lí.

- Hãy chứng minh định lí trên.

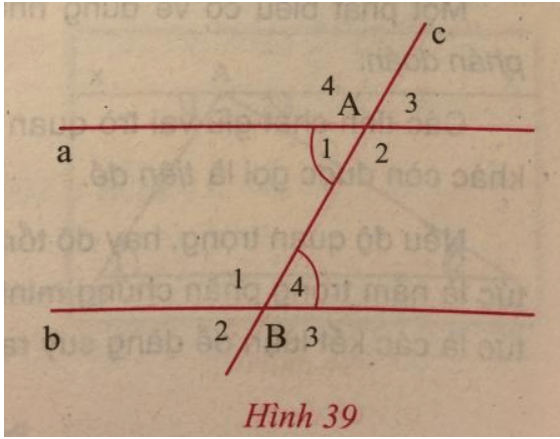
b) Cho định lí: Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì các góc đồng vị bằng nhau.

- Hãy cho biết giả thiết của định lí.

- Hãy cho biết kết luận của định lí.

- Hãy chứng minh định lí trên.

Lời giải:

a)

- Giả thiết của định lí là: "góc tạo bởi hai tia phân giác của hai góc kề bù".

- Kết luận của định lí là: "một góc vuông".

- Chứng minh định lí:

 

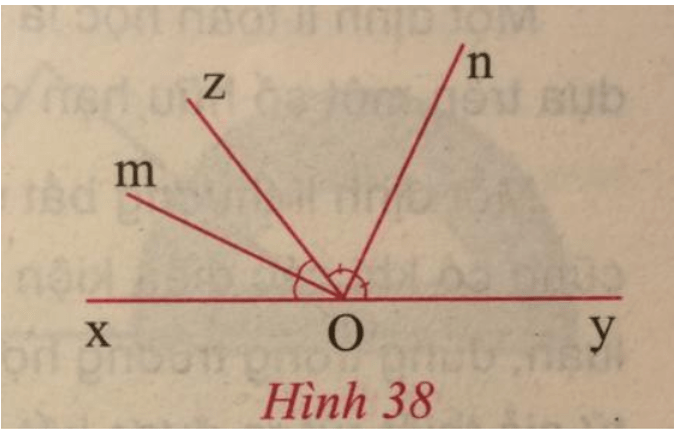
b)

- Giả thiết của định lí là: "một đường thẳng cắt hai đường thẳng phân biệt và trong các góc tạo thành có một cặp góc so le trong bằng nhau".

- Kết luận của định lí là: "các góc đồng vị bằng nhau".

- Chứng minh định lí:

Giả sử đường thẳng c cắt hai đường thẳng phân biệt a và b tương ứng tại các điểm A và B,

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải Toán 7 VNEN Bài 5: Định Lí file PDF hoàn toàn miễn phí.