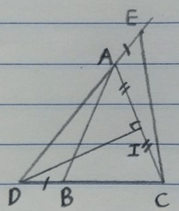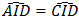Giải Toán lớp 7 VNEN Bài 6: Tính chất ba đường trung trực của tam giác

Hướng dẫn Giải bài tập Toán VNEN Bài 6: Tính chất ba đường trung trực của tam giác trang 83 Hình học Tập 2 chương 3 sách giáo khoa lớp 7 chương trình mới chính xác, ngắn gọn và dễ hiểu dưới đây sẽ giúp các em học sinh trả lời các câu hỏi và giải các bài toán nhanh chóng, tiếp thu bài học trên lớp tốt hơn.

A.B. Hoạt động khởi động và hình thành kiến thức Bài 6: Tính chất ba đường trung trực của tam giác

Câu 2. (trang 83 SGK Toán lớp 7 VNEN chương 3 tập 2)

a) b) (Sgk)

c) Đọc và làm theo yêu cầu

Thực hiện chứng minh tính chất thông qua việc điền vào các chỗ trống dưới đây:

- Vì O nằm trên đường trung trực của đoạn thẳng AC nên OA = OC (1)

- Vì O nằm trên đường trung trực của đoạn thẳng AB nên OA = .......... (2)

Từ (1) và (2) suy ra ............. = ............. ( = OA)

Do đó điểm O nằm trên đường ............ của cạnh BC (theo tính chất đường trung trực).

Vậy ba đường trung trực của tam giác ABC cùng đi qua điểm O và ta có OA = OB = OC.

Trả lời:

Điền lần lượt như sau: OB ; OB; OC và trung trực.

C. Hoạt động luyện tập Bài 6: Tính chất ba đường trung trực của tam giác

Câu 1. (trang 83 SGK Toán 7 VNEN chương 3 tập 2)

Cho tam giác ABC cân tại đỉnh A, trung trực của cạnh AC cắt CB tại điểm D (D nằm ngoài đoạn BC). Trên tia đối tia AD lấy E sao cho AE = BD. Chứng minh tam giác DCE cân. (Gợi ý: Cần chứng minh CD = CE).

Trả lời:

Gọi I là trung điểm của AC

Xét 2 tam giác ADI và CDI, ta có:

- AI = IC

- 

- DI chung

Suy ra : ΔADI = ΔCDI (c.g.c) ⇒ 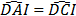 (cặp góc tương ứng)

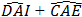
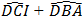
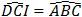
Ta có: - = 180 độ (kề bù)

-  = 180 độ ( vì (ΔABC cân tại A), mà = 180 độ (kề bù)

Lại có: Ta có: (chứng minh trên)

Suy ra: 

Xét tam giác ABD và CAE, có:

- DB = EA (gt)

-  (chứng minh trên)

- AB = AC

Suy ra: ΔDBA = ΔCAE (c.g.c)

⇒ AD = CE (1)

mà AD = CD (ΔADI = ΔCDI) (2)

Từ (1) và (2) ⇒ DC = CE ⇒ Tam giác DCE cân tại C

Câu 2. (trang 83 SGK VNEN Toán lớp 7 chương 3 tập 2)

Cho tam giác ABC có AB < AC, lấy E trên cạnh CA sao cho CE = BA, các đường trung trực của các đoạn thẳng BE và CA cắt nhau ở I.

a) Chứng minh: ΔAIB = ΔCIE

b) Chứng minh: AI là tia phân giác vỉa góc BAC.

Trả lời:

a) Ta có:

- ΔBIE cân tại I (vì IH là trung trực của BE)

⇒ IB = IE

- ΔAIC cân tại I (vì IK là trung trực của AC)

⇒ IA = IC

Xét ΔAIB và ΔEIC, có:

- IB = IE

- CE = BA

- IA = IC

Suy ra: ΔAIB = ΔEIC (c.c.c)

b) ΔAIB = ΔEIC (câu a) suy ra

- (1)

mà (vì tam giác AIC cân tại I) (2)

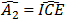
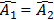
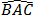
Từ (1) và (2) suy ra:  ⇒ OA là tia phân giác của (đpcm)

D.E. Hoạt động vận dụng và tìm tòi mở rộng Bài 6: Tính chất ba đường trung trực của tam giác

Câu 3. (trang 83 SGK Toán VNEN 7 chương 3 tập 2)

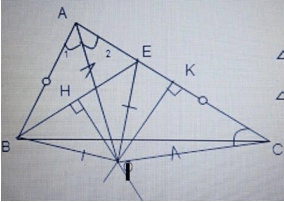
Cho hình 57. chứng minh ba điểm B, K, C thẳng hàng.

Trả lời:

- Lần lượt nối K với B, A và C, ta có:

+) DK là trung trực của AB

+) EK là trung trực của AC

Do đó ΔAKE = ΔCKE (c.c.c)

⇒  ⇒ EK là phân giác của góc  (1)

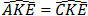
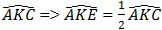
Tương tự ta có: ΔBKD = ΔAKD (c.c.c)

   và KD là phân giác của góc 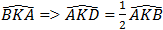(2)

Mà 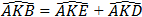= 90 độ (vì ADKE là hcn) (3)

Từ (1) , (2) và (3) suy ra: 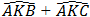= 180 độ ⇒ B, K và C thẳng hàng (đpcm)

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải Toán 7 VNEN Bài 6: Tính chất ba đường trung trực của tam giác  file PDF hoàn toàn miễn phí.