Giải SBT Toán 6 bài 4 Hình học tập 2 chương 2: Khi nào thì xOy + yOz = xOz

Hướng dẫn giải sách bài tập Toán lớp 6 Hình học tập 2 bài 4: Khi nào thì xOy + yOz = xOz kèm công thức và lời giải chi tiết cho từng bài tập giúp các em học sinh ôn tập các dạng bài xoay quanh chương 2: Góc. Mời các em tham khảo lời giải chi tiết dưới đây.

Giải câu 1 bài 4 Hình học SBT Toán lớp 6 tập 2

Gọi Oz là tia nằm giữa hai tia Ox, Oy.

Biết ∠(xOy) = a^o, ∠(zOx) = b^o. Tính (yOz)

Đáp án:

Vì tia Oz nằm giữa hai tia Ox, Oy nên:

∠(xOy) = ∠(yOz) + ∠(xOz) ⇒ ∠(yOz) = ∠(xOy) - ∠(xOz) = a^o – b^o

Giải câu 2 bài 4 Toán lớp 6 Hình học tập 2 SBT

Cho biết ∠(LPM) = 90^o. Vẽ tia PU để ∠(LPM) = ∠(LPU) + ∠(UPM)

Đáp án:

Lấy điểm U nằm trong góc LPM, Vẽ tia PU. Vì tia PU nằm giữa hai tia PL và PM nên: ∠(LPM) = ∠(LPU) + ∠(UPM)

Như hình vẽ bên:

Giải câu 3 bài 4 Toán lớp 6 SBT tập 2 Hình học

Ở hình dưới, hai tia OI , OK đối nhau. Tia OI cắt đoạn thẳng AB tại I. Biết ∠(KOA) = 120^o, ∠(BOI) = 45^o

Tính ∠(KOB), ∠(AOI), ∠(BOA)

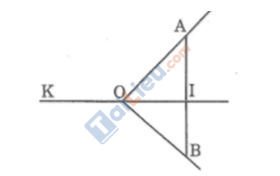
Đáp án:

Vì ∠(KOB) và ∠(BOI) kề bù nên ∠(KOB) + ∠(BOI) = 180^o

Suy ra: ∠(KOB) = 180o - ∠(BOI) = 180^o – 45o = 135^o

Vì ∠(KOA) và ∠(AOI) kề bù nên ∠(KOA) + ∠(AOI) = 180^o

Suy ra: ∠(AOI) = 180 - ∠(KOA) = 180^o – 120^o = 60^o

Vì tia OI nằm giữa hai tia OA và OB nề:

∠(AOI) + ∠(BOI) = ∠(AOB)

Suy ra : ∠(AOB) = 60^o + 45^o = 105^o

Giải câu 4 bài 4 SBT Toán 6 Hình học tập 2

Xem hình dưới, làm thế nào để chỉ đo hai góc mà biết được số đo của cả ba góc xOy, xOz, yOz

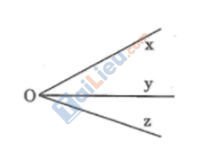
Đáp án:

Trong hình vẽ, tia Oy nằm giữa hai tia Ox và Oz nên:

∠(xOz) = ∠(xOy) + ∠(yOz)

Do vậy, ta chỉ cần đo hai góc (xOy) và (yOz) rồi suy ra góc (xOz) hoặc đo hai góc (xOy) và (xOz) rồi suy ra góc (yOz)

Giải câu 5 bài 4 Hình học Toán 6 tập 2 SBT

Xem hình dưới. Hỏi ∠(tOv) có phải là góc vuông hay không? Vì sao?

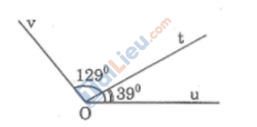
Đáp án:

Vì tia Ot nằm giữa hai tia Ou và Ov nên:

∠(uOt) = ∠(tOv) + ∠(uOv)

Suy ra: ∠(tOv) = ∠(uOv) - ∠(uOt) = 129^o – 39^o = 90^o

Vậy ∠(tOv) là góc vuông

Giải câu 6 bài 4 Toán 6 SBT tập 2 Hình học

Tia Oy nằm giữa hai tia Ox và Oz. Biết ∠(xOy) = 40^o. Hỏi góc xOz là nhọn, vuông, tù hay bẹt nếu số đo của góc yOz lần lượt bằng 30^o, 50^o, 70^o, 140^o

Đáp án:

Vì tia Oy nằm giữa hai tia Ox và Oz nên:

∠(xOz) = ∠(xOy) + ∠(yOz)

Ta có: ∠(xOy) = 40^o, nếu số đo của ∠(yOz) lần lượt bằng 30^o, 50^o, 70^o, 140^o

Thì:

∠(yOz) = 30^o; ∠(xOz) = 40^o + 30^o = 70^o; ∠(xOz) là góc nhọn

∠(yOz) = 50^o; ∠(xOz) = 40^o + 50^o = 90^o; ∠(xOz) là góc vuông

∠(yOz) = 70^o; ∠(xOz) = 40^o + 70^o = 110^o; ∠(xOz) là góc tù

∠(yOz) = 140^o; ∠(xOz) = 40^o + 140^o = 180^o; ∠(xOz) là góc bẹt

Giải câu 7 bài 4 SBT Hình học Toán lớp 6 tập 2​​​​​​​

Trên đường thẳng d từ trái sang phải ta lấy các điểm A, D, C, B và lấy điểm O nằm ngoài đường thẳng d.

Biết: ∠(AOD) = 30^o , ∠(DOC) = 40^o; ∠(AOB) = 90^o. Tính ∠(AOC), ∠(COB), ∠(DOB)

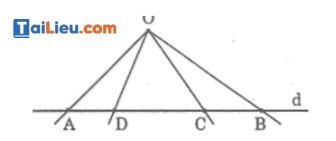
Đáp án:

Vì D nằm giữa A và C nên tia OD nằm giữa hai tia OA và OC.

Suy ra: ∠(AOC) = ∠(AOD) + ∠(DOC) = 30^o + 40^o = 70^o

Vì C nằm giữa A và B nên tia OB nằm giữa hai tia OA và OB.

Suy ra: ∠(AOB) = ∠(AOC) + ∠(COB)

⇒∠(COB) = ∠(AOB) - ∠(AOC) = 90^o - 70^o = 20^o

Vì D nằm giữa A và B nên tia OD nằm giữa hai tia OA và OB.

Suy ra: ∠(AOB) = ∠(AOD) + ∠(DOB)

⇒∠(DOB) = ∠(AOB) - ∠(AOD) = 90^o - 30^o = 60^o

►► CLICK NGAY vào nút TẢI VỀ dưới đây để download Giải sách bài tập toán lớp 6 bài 4 tập 2 chương 2 file word, pdf hoàn toàn miễn phí.