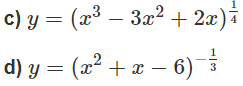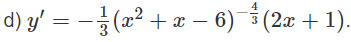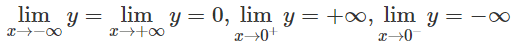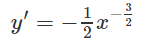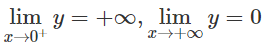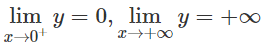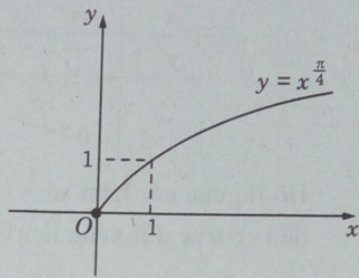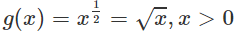Giải SBT toán 12 trang 104 tập 1 Bài 2 đầy đủ

Với bộ tài liệu giải sách bài tập toán 12 tập 1 Bài 2: Hàm số lũy thừa, hướng dẫn cách giải chi tiết cho từng câu hỏi, từng phần học bám sát nội dung chương trình SBT bộ môn Toán lớp 12. Nội dung chi tiết các em xem tại đây.

Giải Bài 2.6 trang 104 SBT toán 12 tập 1

Tìm tập xác định của các hàm số sau:

 

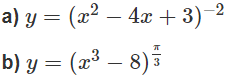
Lời giải:

a) Hàm số xác định khi x² − 4x + 3 ≠ 0 hay x ≠ 1; x ≠ 3.

Vậy tập xác định của hàm số đã cho là R \ {1;3}.

b) Hàm số xác định khi x³ – 8 > 0 hay x > 2. Vậy tập xác định là (2; +∞).

c) Hàm số xác định khi x³ – 3x² + 2x > 0 hay x(x – 1)(x – 2) > 0

Suy ra 0 < x < 1 hoặc x > 2. Vậy tập xác định là (0;1) ∩ (2;+∞)

d) Hàm số xác định khi x² + x – 6 > 0 hay x < -3 và x > 2.

Vậy tập xác định là (−∞; −3) ∪ (2; +∞).

Giải Bài 2.7 trang 104 SBT toán 12 tập 1

Tính đạo hàm của các hàm số cho ở bài 2.6

Lời giải:

   

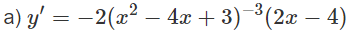
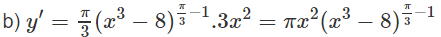
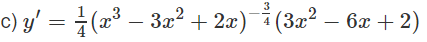
Giải Bài 2.8 trang 104 SBT toán 12 tập 1

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:

Lời giải:

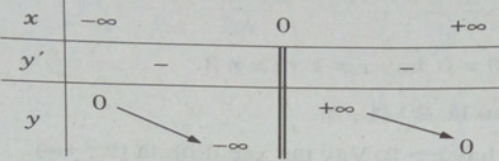
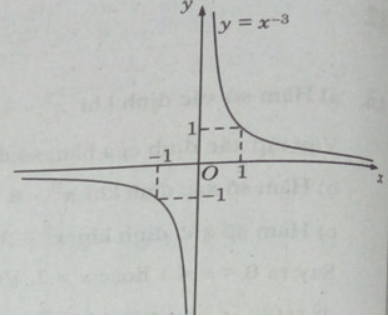
a) Tập xác định: R\{0}

Hàm số đã cho là hàm số lẻ.

Ta có: y′ < 0, ∀ x ∈ R \ {0} nên hàm số luôn nghịch biến trên các khoảng xác định.

Đồ thị có tiệm cận ngang là trục hoành, tiệm cận đứng là trục tung.

Bảng biến thiên:

Đồ thị của hàm số có tâm đối xứng là gốc tọa độ.

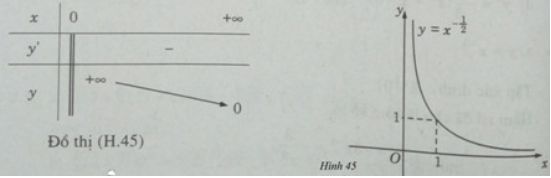
b) Tập xác định: D = (0; +∞)

Vì y' < 0 ∀ x ∈ D nên hàm số nghịch biến.

Đồ thị có tiệm cận đứng là trục tung, tiệm cận ngang là trục hoành.

Bảng biến thiên:

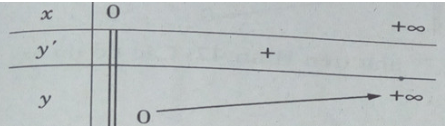
c) Tập xác định: D = (0; +∞)

y′ > 0, ∀ x ∈ D

Vì y′ > 0, ∀ x ∈ D nên hàm số nghịch biến.

Đồ thị không có tiệm cận.

Bảng biến thiên

Đồ thị

Giải Bài 2.9 trang 104 SBT toán 12 tập 1

Vẽ đồ thị của các hàm số y = x² và 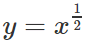 trên cùng một hệ trục tọa độ. Hãy so sánh giá trị của các hàm số đó khi x = 0,5; 1; 3/2; 2; 3; 4.

Lời giải:

Đặt f(x) = x², x ∈ R

Đồ thị:

​​​​​​​

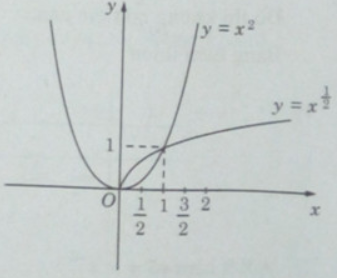
Từ đồ thị của hai hình đó ta có:

f(0,5) < g(0,5);

f(1) = g(1) = 1;

f(3/2) > g(3/2), f(2) > g(2);

f(3) > g(3), f(4) > g(4).

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về giải bài tập SBT toán 12 tập 1 Bài 2: Hàm số lũy thừa, file PDF hoàn toàn miễn phí.