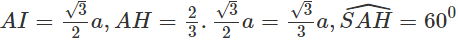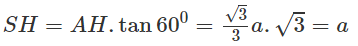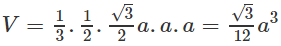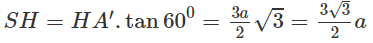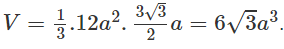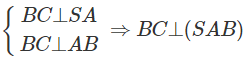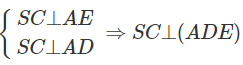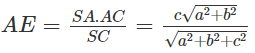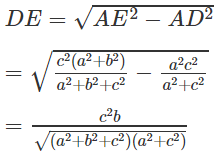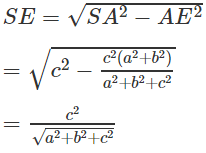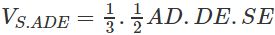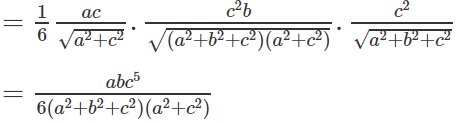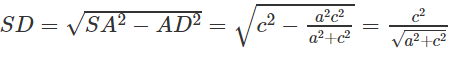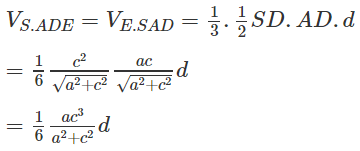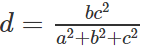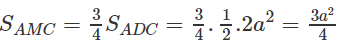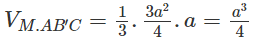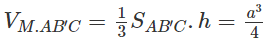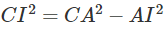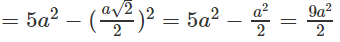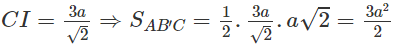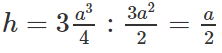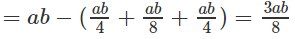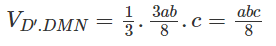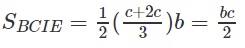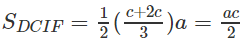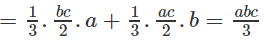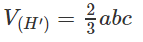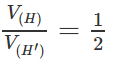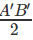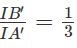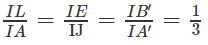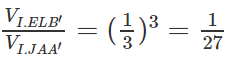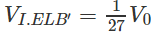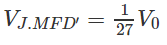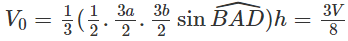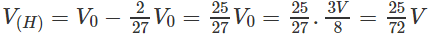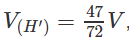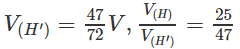Giải SBT Toán hình 12 trang 18, 19 tập 1 Bài 3 đầy đủ

Với bộ tài liệu giải sách bài tập toán Hình học 12 tập 1 Bài 3: Khái niệm về thể tích của khối đa diện, hướng dẫn cách giải chi tiết cho từng câu hỏi, từng phần học bám sát nội dung chương trình SBT bộ môn Toán lớp 12. Nội dung chi tiết các em xem tại đây.

Giải Bài 1.10 trang 18 SBT toán 12 tập 1

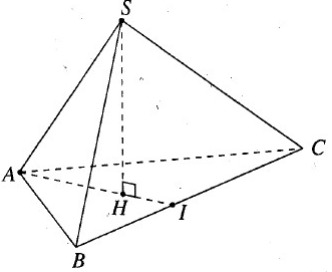
Cho khối chóp tam giác đều S.ABC có đáy là tam giác đều cạnh bằng a, các cạnh bên tạo với đáy một góc 60^o. Hãy tính thể tích của khối chóp đó.

Lời giải:

Kẻ SH ⊥ (ABC). Đường thẳng AH cắt BC tại I.

Do S.ABC là hình chóp tam giác đều nên H là trọng tâm của ΔABC.

Do đó

Thể tích khối chóp S.ABC là:

Giải Bài 1.11 trang 18 SBT toán 12 tập 1

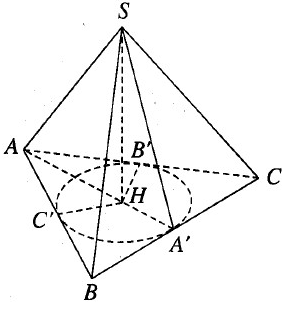
Cho khối chóp S.ABC có đáy là tam giác cân, AB = AC = 5a, BC = 6a và các mặt bên tạo với đáy một góc 60^o. Hãy tính thể tích của khối chóp đó.

Lời giải:

Kẻ SH ⊥ (ABC) và HA’, HB’ , HC’ lần lượt vuông góc với BC, CA, AB. Theo định lí ba đường vuông góc ta có SA′ ⊥ BC, SB′ ⊥ CA, SC′ ⊥ AB

Từ đó suy ra ∠SA′H = ∠SB′H = ∠SC′H = 60^o.

Do đó các tam giác vuông SHA’ , SHB’ , SHC’ bằng nhau. Từ đó suy ra HA’ = HB’ = HC’ . Vậy H là tâm đường tròn nội tiếp tam giác ABC. Do tam giác cân ở A nên AH vừa là đường phân giác , vừa là đường cao, vừa là đường trung tuyến. Từ đó suy ra A, H, A’ thẳng hàng và A’ là trung điểm của BC.

Do đó, AA’² = AB² – BA’² = 25a² – 9a² = 16a²

Vậy AA’ = 4a

Gọi p là nửa chu vi của tam giác ABC, r là bán kính đường tròn nội tiếp của nó.

Khi đó SABC = 6a.4a/2 = 12a2 = pr = 8ar

Từ đó suy ra r = 3a/2

Do đó

Thể tích khối chóp là:

Giải Bài 1.12 trang 18 SBT toán 12 tập 1

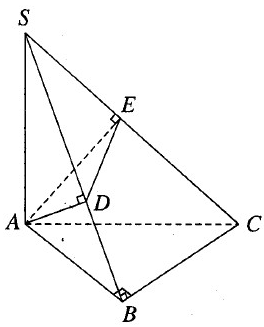
Cho hình chóp tam giác S.ABC có đáy là tam giác vuông ở B. Cạnh SA vuông góc với đáy. Từ A kẻ các đoạn thẳng AD vuông góc với SB và AE vuông góc với SC. Biết rằng AB = a, BC = b, SA = c.

a) Hãy tính thể tích khối chóp S.ADE

b) Tính khoảng cách từ E đến mặt phẳng (SAB).

Lời giải:

a) Ta có

Vì AD ⊂ (SAB) nên AD ⊥ BC

Mặt khác AD ⊥ SB nên AD ⊥ (SBC)

Từ đó suy ra AD ⊥ SC

⇒ SC ⊥ DE hay SE ⊥ (ADE)

Trong tam giác vuông SAB ta có: SA.AB = AD.SB

Tương tự, trong tam giác vuông SAC ta có:

Do AD ⊥ (SBC) nên AD ⊥ DE. Từ đó suy ra:

Vậy

b) Gọi d là khoảng cách từ E đến mặt phẳng (SAB)

Ta có:

Kết hợp với kết quả trong câu a)

ta suy ra 

Giải Bài 1.13 trang 18 SBT toán 12 tập 1

Chứng minh rằng tổng các khoảng cách từ một điểm bất kì trong một tứ diện đều đến các mặt phẳng của nó là một số không đổi.

Lời giải:

Ta có tứ diện đều ABCD, M là một điểm trong của nó. Gọi V là thể tích, S là diện tích mỗi mặt của tứ diện đều ABCD, h_A, h_B, h_C, h_D lần lượt là khoảng cách từ M đến các mặt (BCD), (CDA), (DAB), (ABC).

Khi đó ta có:

V = V_MBCD + V_MCDA + V_MDAB + V_MABCV

= S(h_A + h_B + h_C + h_D)/3

Từ đó suy ra h_A + h_B + h_C + h_D = 3V/S

Giải Bài 1.14 trang 18 SBT toán 12 tập 1

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = 2a, AA’ = a. Lấy điểm M trên cạnh AD sao cho AM = 3MD.

a) Tính thể tích khối chóp M.AB’C

b) Tính khoảng cách từ M đến mặt phẳng (AB’C).

Lời giải:

a) Thể tích khối chóp M.AB’C bằng thể tích khối chóp B’AMC. Ta có:

Do đó

b) Gọi h là khoảng cách từ M đến mặt phẳng (AB’C)

Khi đó

Vì AC² = B’C² = 5a² nên tam giác ACB’ cân tại C. Do đó, đường trung tuyến CI của tam giác ACB’ cũng là đường cao.

Ta có:

Do đó

Từ đó suy ra

Giải Bài 1.15 trang 19 SBT toán 12 tập 1

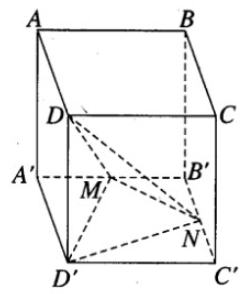
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi M và N theo thứ tự là trung điểm của A’B’ và B’C’. Tính tỉ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’

Lời giải:

Thể tích khối chóp D’.DMN bằng thể tích khối chóp D.D’MN

Ta có: S_D′MN = S_{A′B′C′D′} − (S_D′A′M + S_D′C′N + S_B′MN)

Thể tích khối chóp

Từ đó suy ra tỷ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’ bằng 1/8

Giải Bài 1.16 trang 19 SBT toán 12 tập 1

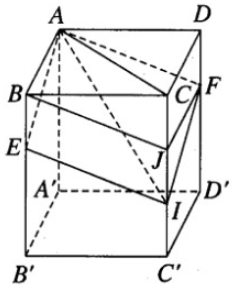
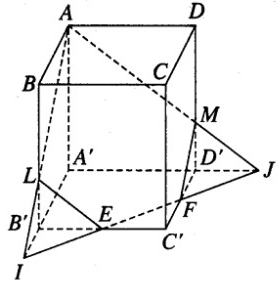
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi E và F lần lượt là những điểm thuộc cạnh BB’ và DD’ sao cho BE = EB′/2, DF = FD′/2. Mặt phẳng (AEF) chia khối hộp chữ nhật ABCD.A’B’C’D’ thành hai khối đa diện (H) và (H’). Gọi (H’) là khối đa diện chứa đỉnh A’. Hãy tính thể tích của (H) và tỉ số thể tích của (H) và (H’).

Lời giải:

Giả sử (AEF) cắt CC’ tại I. Khi đó ta có AE// FI, AF // EI nên tứ giác AEIF là hình bình hành. Trên cạnh CC’ lấy điểm J sao cho CJ = DF. Vì CJ song song và bằng DF nên JF song song và bằng CD. Do đó tứ giác CDFJ là hình chữ nhật. Từ đó suy ra FJ song song và bằng AB. Do đó AF song song và bằng BJ. Vì AF cũng song song và bằng EI nên BJ song song và bằng EI.

Từ đó suy ra IJ = EB = DF = JC = c/3

Ta có

Nên V_(H) = V_A.BCIE + V_A.DCIF

Vì thể tích khối hộp chữ nhật ABCD.A’B’C’D’ bằng abc nên

Từ đó suy ra 

Giải Bài 1.17 trang 19 SBT toán 12 tập 1

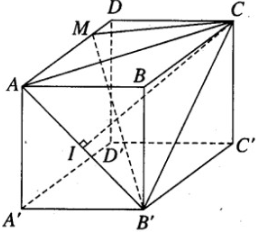
Cho hình hộp ABCD.A’B’C’D’ . Gọi E và F lần lượt là trung điểm của B’C’ và C’D’ . Mặt phẳng (AEF) chia hình hộp đó thành hai hình đa diện (H) và (H’), trong đó (H) là hình đa diện chứa đỉnh A’. Tính tỉ số giữa thể tích hình đa diện (H) và thể tích hình đa diện (H’).

Lời giải:

Giả sử đường thẳng EF cắt đường thẳng A’B’ tại I và cắt đường thẳng A’D’ tại J. AI cắt BB’ tại L, AJ cắt DD’ tại M. Gọi V0 là thể tích khối tứ diện AA’IJ. V là thể tích khối hộp ABCD.A’B’C’D’

Vì EB’ = EC’ và B’I // C’F

nên IB′ = FC′ = 

Do đó 

Để ý rằng BE’ // A’J , B’L // AA’

Ta có

Từ đó suy ra:

Do đó 

Tương tự 

Gọi AB = a, BC = b , đường cao hạ từ A xuống (A’B’C’D’) là h thì

V = V_{ABCD.A′B′C′D′} = h_ab.sin∠BAD

Vậy

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về giải SBT toán hình lớp 12 tập 1 Bài 3: Khái niệm về thể tích của khối đa diện, file PDF hoàn toàn miễn phí.