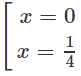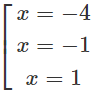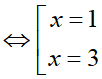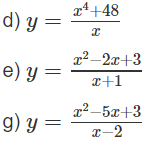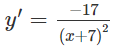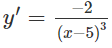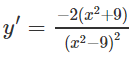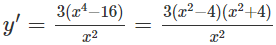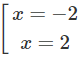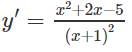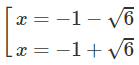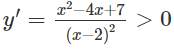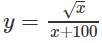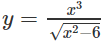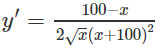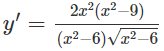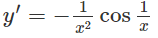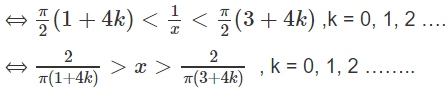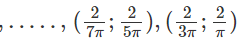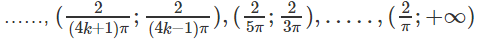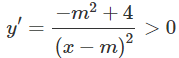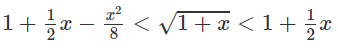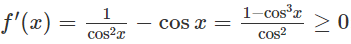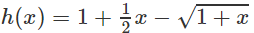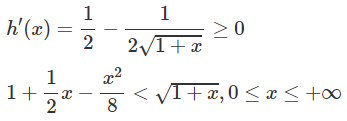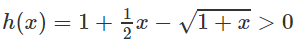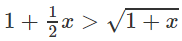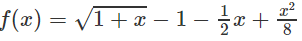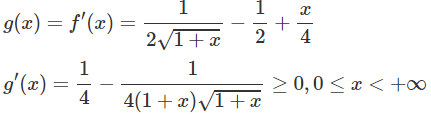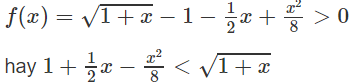Giải SBT toán 12 trang 7, 8 tập 1 Bài 1 đầy đủ

Với bộ tài liệu giải sách bài tập toán 12 tập 1 Bài 1: Sự đồng biến, nghịch biến của hàm số, hướng dẫn cách giải chi tiết cho từng câu hỏi, từng phần học bám sát nội dung chương trình SBT bộ môn Toán lớp 12. Nội dung chi tiết các em xem tại đây.

Giải Bài 1.1 trang 7 SBT toán 12 tập 1

Xét sự đồng biến, nghịch biến của các hàm số:

a) y = 3x² − 8x³

b) y = 16x + 2x² − 16x³/3 − x⁴

c) y = x³ − 6x² + 9x

d) y = x⁴ + 8x² + 5

Lời giải:

a) TXĐ: R

y′ = 6x − 24x² = 6x(1 − 4x)

y' = 0 ⇔ 

y' > 0 trên khoảng (0; 1/4) , suy ra y đồng biến trên khoảng (0; 1/4)

y' < 0 trên các khoảng (-∞; 0 ); (14; +∞), suy ra y nghịch biến trên các khoảng (-∞;0 ); (14;+∞)

b) TXĐ: R

y′ = 16 + 4x − 16x² − 4x³ = −4(x + 4)(x² − 1)

y' = 0 ⇔ 

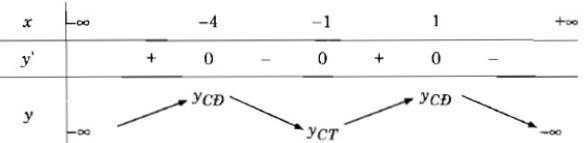
Bảng biến thiên:

Vậy hàm số y đã cho đồng biến trên các khoảng (-∞; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1; +∞)

c) TXĐ: R

y′ = 3x² − 12x + 9

y' = 0 

y' > 0 trên các khoảng (-∞; 1), (3; +∞) nên y đồng biến trên các khoảng (-∞; 1), (3; +∞)

y'< 0 trên khoảng (1; 3) nên y nghịch biến trên khoảng (1; 3)

d) TXĐ: D = R

y′ = 4x³ + 16x = 4x(x² + 4)

y' = 0 ⇔ x = 0

y' > 0 trên khoảng (0; +∞) ⇒ y đồng biến trên khoảng (0; +∞)

y' < 0 trên khoảng (-∞; 0) ⇒ y nghịch biến trên khoảng (-∞; 0)

Giải Bài 1.2 trang 7 SBT toán 12 tập 1

Tìm các khoảng đồng biến, nghịch biến của các hàm số:

 

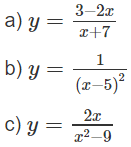
Lời giải:

a) TXĐ: R \ {-7}

y' < 0 trên các khoảng (-∞; -7), (-7; +∞) nên hàm số nghịch biến trên các khoảng đó

b) TXĐ: R \ {5}

y' < 0 trên khoảng (5; +∞) nên y nghịch biến trên khoảng (5; +∞)

y' > 0 trên khoảng (-∞; 5) nên y đồng biến trên khoảng (-∞; 5)

c) TXĐ: R \ {-3; 3}

y' < 0 trên các khoảng (-∞; - 3), (-3; 3), (3; +∞) nên hàm số đã cho nghịch biến trên các khoảng đó.

d) TXĐ: R \ {0}

y' = 0 ⇔ 

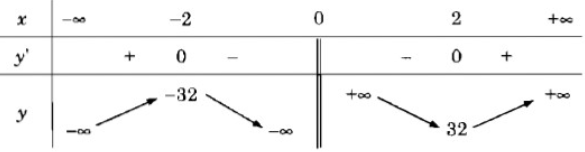
Bảng biến thiên:

Vậy hàm số đã cho đồng biến trên các khoảng (-∞; -2), (2; +∞) và nghịch biến trên các khoảng (-2; 0), (0; 2)

e) TXĐ: R \ {-1}

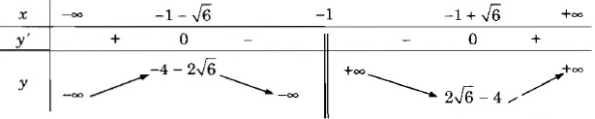
y' = 0 ⇔ 

Vậy hàm số đã cho đồng biến trên các khoảng (−∞; −1 − √6), (−1 + √6; +∞) và nghịch biến trên các khoảng (−1 − √6; −1),(−1; −1 + √6)

g) TXĐ: R \ {2}

(do x² − 4x + 7x² − 4x + 7 có Δ' = - 3 < 0)

Vậy hàm số đã cho đồng biến trên các khoảng (−∞;2),(2;+∞)

Giải Bài 1.3 trang 8 SBT toán 12 tập 1

Xét tính đơn điệu của các hàm số sau:

a) 

b) 

Lời giải:

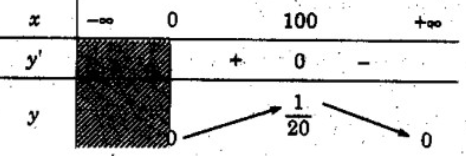
a) TXĐ: [0; +∞)

y’ = 0 ⇔ x = 100

Vậy hàm số đồng biến trên khoảng (0; 100) và nghịch biến trên khoảng (100; +∞)

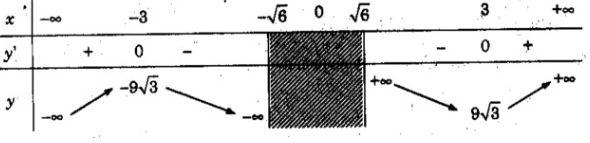
b) TXĐ: (-∞; √6) ∪ (√6; +∞)

y’ = 0 ⇔ x = 3 hoặc x = -3

Vậy hàm số đồng biến trên các khoảng (-∞; -3), (3; +∞), nghịch biến trên các khoảng (-3; −√6 − 6 ), (√6; 3).

Giải Bài 1.4 trang 8 SBT toán 12 tập 1

 

Xét sự đồng biến, nghịch biến của các hàm số:

a) y = x − sinx, x ∈ [0; 2π].

c) y = sin(1/x), (x > 0)

Lời giải:

a) y = x – sinx, x ∈ [0; 2π].

y′ = 1 – cosx ≥ 0 với mọi x ∈ [0; 2π]

Dấu “=” xảy ra chỉ tại x = 0 và x = 2π.

Vậy hàm số đồng biến trên đoạn [0; 2π].

c) Xét hàm số y = sin(1/x) với x > 0.

Giải bất phương trình sau trên khoảng (0; +∞):

 

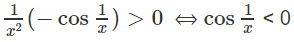
Do đó, hàm số đồng biến trên các khoảng

 

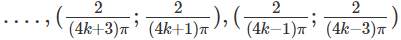
Và nghịch biến trên các khoảng

với k = 0, 1, 2 …

 

Giải Bài 1.5 trang 8 SBT toán 12 tập 1

Xác định tham số m để hàm số sau:

a) 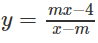 đồng biến trên từng khoảng xác định;

b) y = −x³ + mx² − 3x + 4 nghịch biến trên.

Lời giải:

a) Tập xác định: D = R \ {m}

Hàm số đồng biến trên từng khoảng (−∞; m), (m; +∞) khi và chỉ khi:

⇔ − m² + 4 > 0

⇔ m² < 4 ⇔ −2 < m < 2

c) Tập xác định: D = R

Hàm số nghịch biến trên R khi và chỉ khi:

y′ = −3x² + 2mx – 3 ≤ 0

⇔ y′ = m² – 9 ≤ 0

⇔ m² ≤ 9 ⇔ −3 ≤ m ≤ 3

Giải Bài 1.6 trang 8 SBT toán 12 tập 1

Chứng minh các phương trình sau có nghiệm duy nhất

3(cosx − 1) + 2sinx + 6x = 0

Lời giải:

Đặt y = 3(cos x – 1) + 2sinx + 6

Hàm số xác định, liên tục và có đạo hàm tại mọi x ∈ R

Ta có: y(π) = 0 và y' = -3sin x + 2cos x + 6 > 0, x ∈ R.

Hàm số đồng biến trên R và có một nghiệm x = π

Vậy phương trình đã cho có một nghiệm duy nhất.

Giải Bài 1.7 trang 8 SBT toán 12 tập 1

Chứng minh các bất đẳng thức sau:

a) tanx > sinx, 0 < x < π/2

b) 

với 0 < x < +∞

Lời giải:

a) Xét hàm số f(x) = tanx − sinx trên nửa khoảng [0; π/2);

x ∈ [0;1/2)

Dấu “=” xảy ra khi x = 0.

Suy ra f(x) đồng biến trên nửa khoảng [0; π/2)

Mặt khác, ta có f(0) = 0, nên f(x) = tanx – sinx > 0 hay tanx > sinx với mọi x ∈ [0; 1/2)

b) Xét hàm số h(x) trên [0; +∞)

Dấu “=” xẩy ra chỉ tại x = 0 nên h(x) đồng biến trên nửa khoảng [0; +∞).

Vì h(x) = 0 nên

Hay

Xét hàm số trên f(x) trên [0; +∞);

Vì g(0) = 0 và g(x) đồng biến trên nửa khoảng [0; +∞) nên g(x) ≥ 0, tức là f′(x) ≥ 0 trên khoảng đó và vì dấu “=” xảy ra chỉ tại x = 0 nên f(x) đồng biến trên nửa khoảng .

Mặt khác, ta có f(0) = 0 nên

Với mọi 0 < x < +∞.

Giải Bài 1.8 trang 8 SBT toán 12 tập 1

 

Xác định giá trị của b để hàm số f(x) = sinx – bx + c nghịch biến trên toàn trục số.

Lời giải:

f(x) = sinx – bx + c nghịch biến trên R nếu ta có:

f′(x) = cosx – b ≤ 0, ∀ x ∈ R.

Vì |cosx| ≤ 1| nên f′(x) ≤ 0, ∀ x ∈ R ⇔ b ≥ 1.

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về giải bài tập SBT toán 12 tập 1 Bài 1: Sự đồng biến, nghịch biến của hàm số, file PDF hoàn toàn miễn phí.