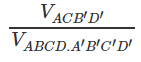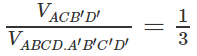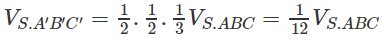Giải SBT Toán Hình học 12 trang 19, 20 tập 1 Câu hỏi và bài tập chương 1 đầy đủ

Với bộ tài liệu giải sách bài tập toán Hình học 12 tập 1 Câu hỏi và bài tập chương 1, hướng dẫn cách giải chi tiết cho từng câu hỏi, từng phần học bám sát nội dung chương trình SBT bộ môn Toán lớp 12. Nội dung chi tiết các em xem tại đây.

Giải Bài 1.18 trang 207 SBT toán 12 tập 1

Nêu hai tính chất đặc trưng của hình đa diện

Lời giải:

a) Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc một cạnh chung.

b) Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.

Giải Bài 1.19 trang 207 SBT toán 12 tập 1

Tìm trong thực tế một ví dụ về một hình đa diện

Lời giải:

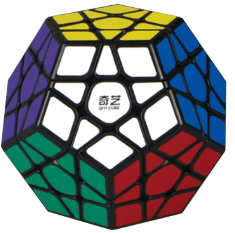
Ví dụ về chiếc Rubik:

 

Giải Bài 1.20 trang 19 SBT toán 12 tập 1

Tìm một ví dụ một hình tạo bởi các hình đa giác nhưng không phải là hình đa diện

Lời giải:

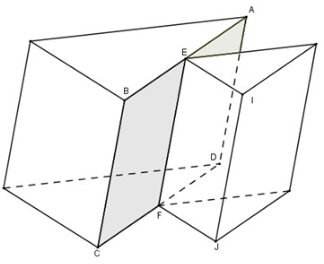
Ví dụ, hình sau được tạo bởi các đa giác nhưng không phải là một đa diện. Vì EF là giao của hai đa giác ABCD và EFJI nhưng nó không phải là cạnh chung của hai đa giác đó.

Giải Bài 1.21 trang 19 SBT toán 12 tập 1

Thế nào là hai đa diện bằng nhau? Tìm một ví dụ về hai đa diện bằng nhau.

Lời giải:

- Hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến đa diện này thành đa diện kia.

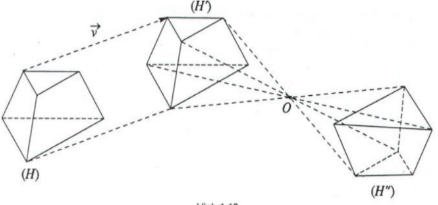
- Ví dụ về đa diện bằng nhau:

Giải Bài 1.22 trang 19 SBT toán 12 tập 1

Thế nào là một đa diện lồi? Tìm một ví dụ về một hình đa diện không lồi.

Lời giải:

- Khối đa diện (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của (H) luôn thuộc (H). Khi đó đa diện xác định (H) được gọi là đa diện lồi.

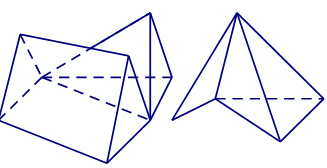
- Ví dụ về hình đa diện không lồi:

Giải Bài 1.23 trang 19 SBT toán 12 tập 1

Thế nào là một hình đa diện đều? Kể tên các loại hình đa diện đều.

Lời giải:

- Một khối đa diện lồi được gọi là khối đa diện đều loại {p;q} nếu:

a) Mỗi mặt của nó là một đa giác đều p cạnh;

b) Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.

- Các loại hình đa diện đều:

    + Khối đa diện loại {3;3} (khối tứ diện đều).

    + Khối đa diện đều loại {3;4} (khối bát diện đều hay khối tám mặt đều)

    + Khối đa diện đều loại {4;3} (khối lập phương)

    + Khối đa diện đều loại {5;3} (khối thập nhị diện đều hay khối mười hai mặt đều)

    + Khối đa diện loại {3;5} (khối nhị thập diện đều hay khối hai mươi mặt đều)

Giải Bài 1.24 trang 19 SBT toán 12 tập 1

Viết công thức tính thể tích hình lăng trụ, hình nón.

Lời giải:

    + Thể tích V của khối chóp có diện tích đáy B và chiều cao h là V = Bh/3.

    + Thể tích V của khối lăng trụ có diện tích đáy B và chiều cao h là V = Bh.

Giải Bài 1.25 trang 19 SBT toán 12 tập 1

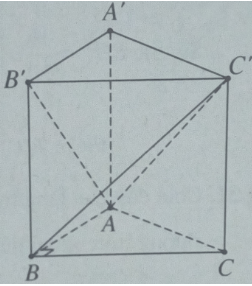
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông ở B, AB = BC = AA’. Hãy chia lăng trụ đó thành ba tứ diện bằng nhau.

Lời giải:

Chia lăng trụ đã cho thành ba tứ diện: ABCC’, ABB’C’ và AA’B’C’. Phép đối xứng qua mặt phẳng (ABC’) biến tứ diện ABCC’ thành tứ diện ABB’C’. Phép đối xứng qua mặt phẳng (AB’C’) biến tứ diện ABB’C’ thành tứ diện AA’B’C’.

Suy ra ba tứ diện đó bằng nhau.

Giải Bài 1.26 trang 19 SBT toán 12 tập 1

Cho hình hộp ABCD.A’B’C’D’. Tính:

Lời giải:

Ta có:

Giải Bài 1.27 trang 20 SBT toán 12 tập 1

Cho khối chóp S.ABC có thể tích bằng V. Gọi B’ và C’ lần lượt là trung điểm của SB và SC, A’ nằm trên SA sao cho SA− = 3SA'−. Tính thể tích khối chóp S.A’B’C’ theo V.

Lời giải:

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về giải SBT toán hình lớp 12 tập 1 Câu hỏi và bài tập chương 1, file PDF hoàn toàn miễn phí.