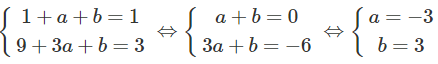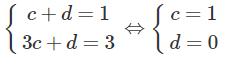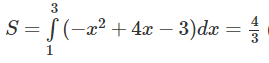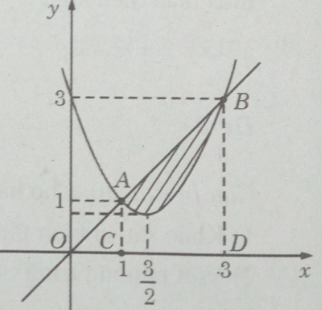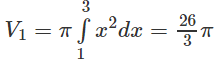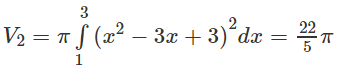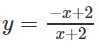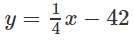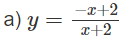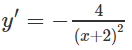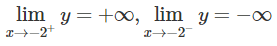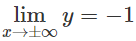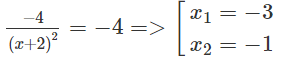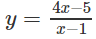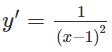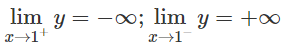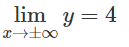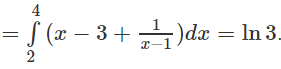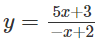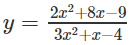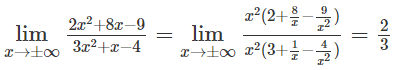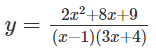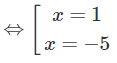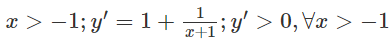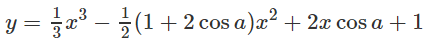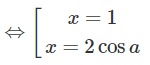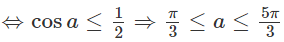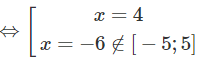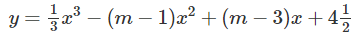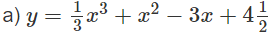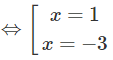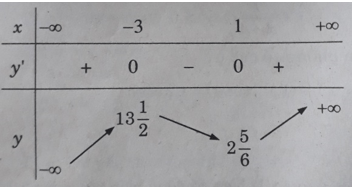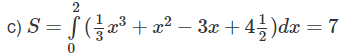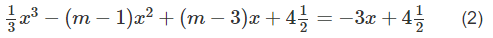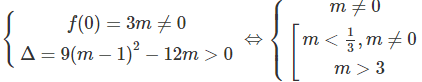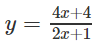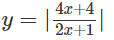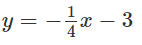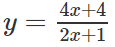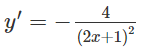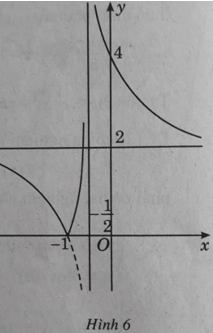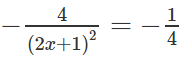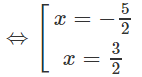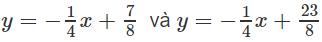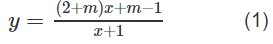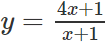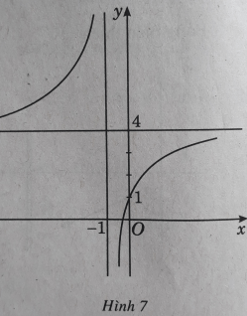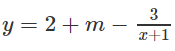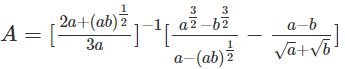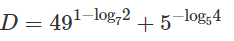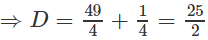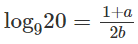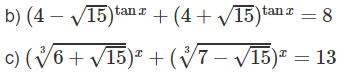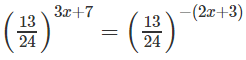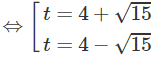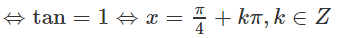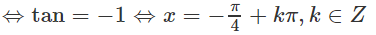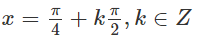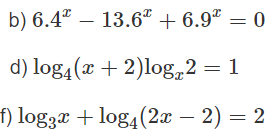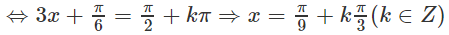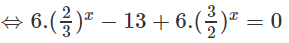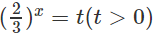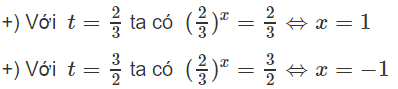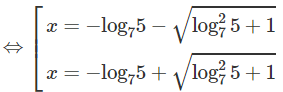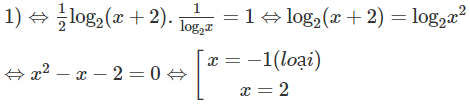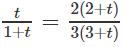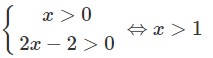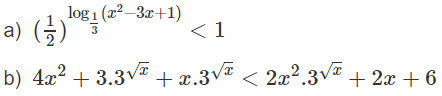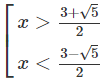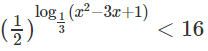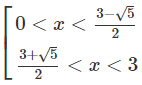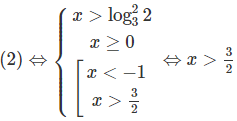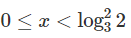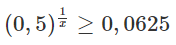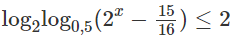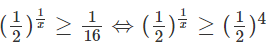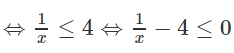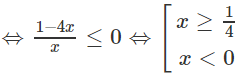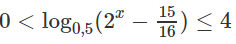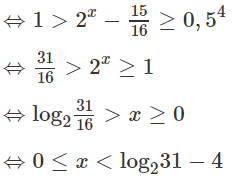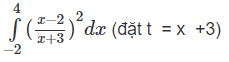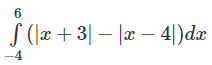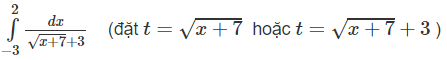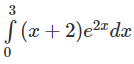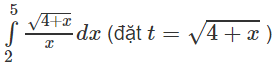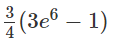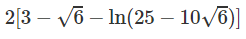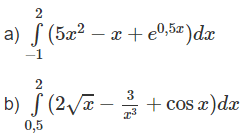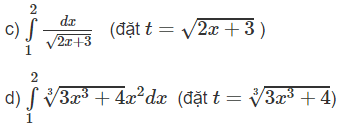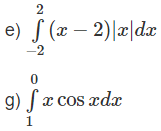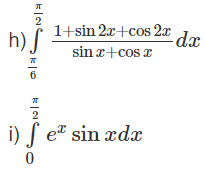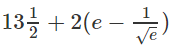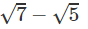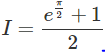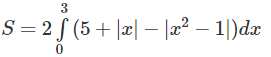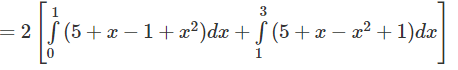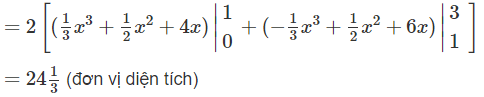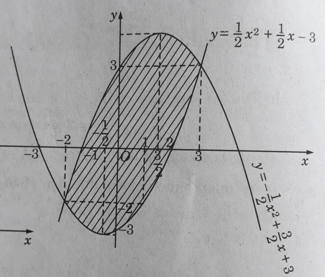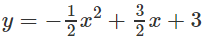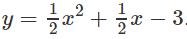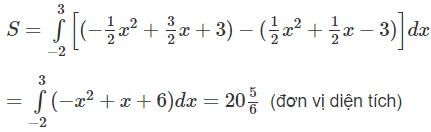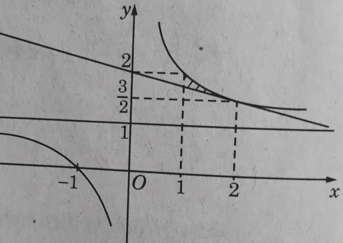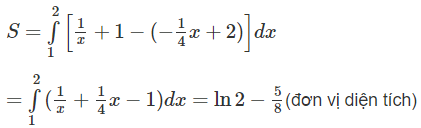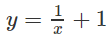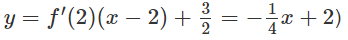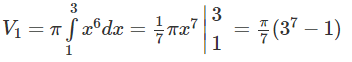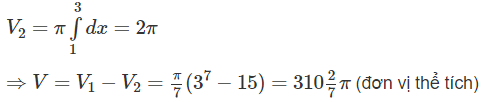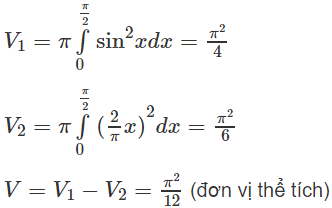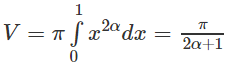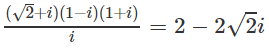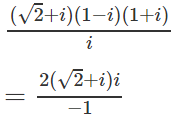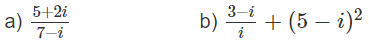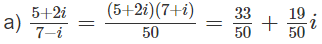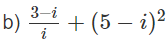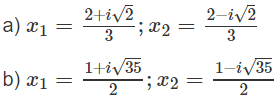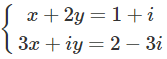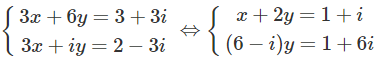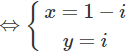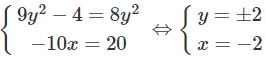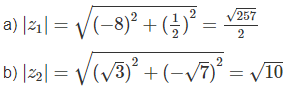Giải SBT Toán 12 trang 216, 217, 218, 219, 220 tập 2 Ôn tập cuối năm

Với bộ tài liệu giải sách bài tập toán 12 tập 2 Ôn tập cuối năm, hướng dẫn cách giải chi tiết cho từng câu hỏi, từng phần học bám sát nội dung chương trình SBT bộ môn Toán lớp 12. Nội dung chi tiết các em xem tại đây.

Giải Bài 1 trang 216 SBT toán 12 tập 1

a) Xác định a, b, c, d để đồ thị của các hàm số:

y = x² + ax + b

và y = cx + d

cùng đi qua hai điểm M(1; 1) và B(3; 3).

b) Vẽ đồ thị của các hàm số ứng với các giá trị a, b, c và d tìm được trên cùng một mặt phẳng tọa độ. Tính diện tích của hình phẳng giới hạn bởi hai đường cong trên.

c) Tính thể tích của vật thể tròn xoay sinh bởi hình phẳng trên quay quanh trục hoành.

Lời giải:

a) a và b thỏa mãn hệ phương trình :

c và d thỏa mãn hệ phương trình:

b) (H.90) Ta có hai hàm số tương ứng là: y = x² – 3x + 3 và y = x

Vậy

c) V = V₁ – V₂, trong đó V₁ là thể tích vật thể tròn xoay sinh ra do quay hình thang ACDB quanh trục Ox, V₂ là thể tích vật thể tròn xoay sinh ra do quay hình thang cong ACDB quanh trục Ox.

Ta có

Vậy

Giải Bài 2 trang 216 SBT toán 12 tập 1

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số:

b) Viết phương trình tiếp tuyến của (C) , biết nó vuông góc với đường thẳng

Lời giải:

    +) Tập xác định: D = R\{-2}

    +) Ta có: 

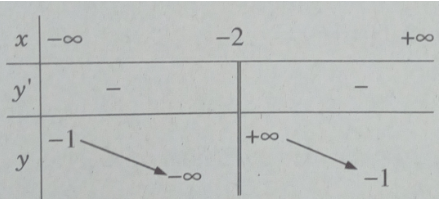
Bảng biến thiên:

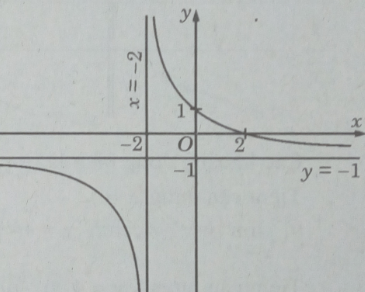
Hàm số nghịch biến trên các khoảng (−∞; −2), (−2; +∞)

    +) Tiệm cận đứng x = -2 vì

Tiệm cận ngang y = -1 vì

Giao với các trục tọa độ: (0; 1); (2; 0)

Đồ thị

b) Tiếp tuyến của đồ thị có hệ số góc k = -4

(vì vuông góc với đường thẳng  )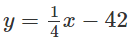

Hoành độ tiếp điểm thỏa mãn phương trình:

Ứng với x₁ = −3, ta có tiếp tuyến y = - 4x – 17

Ứng với x₂ = −1, ta có tiếp tuyến y = - 4x – 1.

Giải Bài 3 trang 216 SBT toán 12 tập 1

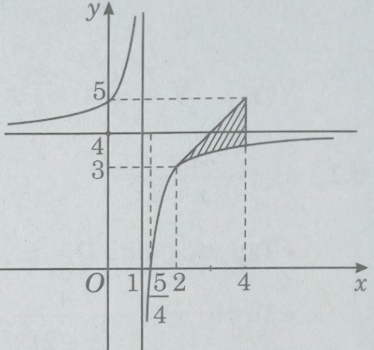
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số:

b) Tính diện tích hình phẳng giới hạn bởi (C), tiếp tuyến của (C) tại A(2; 3) và đường thẳng x = 4.

Lời giải:

a) Tập xác định: D = R\{1}

Đạo hàm: 

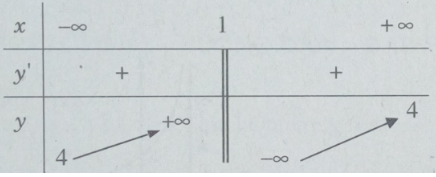
Bảng biến thiên:

Các khoảng đồng biến là (−∞;1) và (1;+∞)

Tiệm cận đứng x = 1 vì

Tiệm cận ngang y = 4 vì

Giao với các trục tọa độ: (0; 5) và (5/4;0)

Đồ thị

b) Ta có: y’(2) = 1. Phương trình tiếp tuyến là y = x + 1

Diện tích của miền cần tìm là:

 

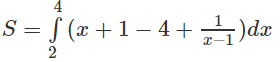
Giải Bài 4 trang 216 SBT toán 12 tập 1

Tìm các đường tiệm cận của đồ thị các hàm số sau:

a) 

b) 

Lời giải:

a) Tiệm cận đứng: x = 2; Tiệm cận ngang: y = -5

b) Ta có:

Vậy đồ thị có đường tiệm cận ngang y = 2/3

Ta có:

Từ đó đồ thị có hai tiệm cận đứng là x = 1 và x = -4/3

Giải Bài 5 trang 216 SBT toán 12 tập 1

Tìm các điểm cực trị của các hàm số sau:

a) y = −x³ − 6x² + 15x + 1

b) y = x + ln(x + 1)

Lời giải:

a) y′ = −3x2 − 12x + 15;

y′′ = −6x – 12;

y′ = 0 ⇔ 3x² + 12x – 15 = 0

y′′(1) = −18 < 0; y′′(−5) = 18 > 0

Vậy với x = -5 hàm số đạt cực tiểu và y_CT = -99

Với x = 1 hàm số đạt cực đại và y_CĐ = 9

b) Tập xác định:

Giải Bài 6 trang 216 SBT toán 12 tập 1

Tìm a ∈ (0; 2π) để hàm số sau đồng biến trên khoảng (1; +∞).

Lời giải:

Tập xác định: D = R; y′ = x² − (1 + 2cosa)x + 2cosa

y′= 0 

Vì y’ < 0 ở ngoài khoảng nghiệm nên để hàm số đồng biến với mọi x > 1 thì 2cosa ≤ 1

(vì a ∈ (0; 2π).

Giải Bài 7 trang 216 SBT toán 12 tập 1

Tìm giá trị lớn nhất và nhỏ nhất của các hàm số sau trên các khoảng, đoạn tương ứng:

a) g(x) = |x3 + 3x2 – 72x + 90| trên đoạn [-5; 5]

b) f(x) = x4 – 4x2 + 1 trên đoạn [-1; 2]

c) f(x) = x – ln x + 3 trên khoảng (0; ∞)

Lời giải:

a) Xét hàm số f(x) = x3 + 3x2 − 72x + 90 trên đoạn [-5;5]

f′(x) =3x2 + 6x − 72;

f′(x) = 0 

f(−5) = 400; f(5) = −70; f(4) = −86

Ngoài ra, f(x) liên tục trên đoạn [-5;5] và f(−5).f(5) < 0 nên tồn tại x₀ ∈ (−5;5) sao cho f(x₀) = 0

Ta có g(x) = |f(x)| ≤ 0 và g(x₀) = |f(x₀)| = 0;

g(−5) = |400| = 400

g(5) = |−70| = 70; g(4) = |f(4)| = |−86| = 86

Vậy min g(x) = g(x₀) = 0; max g(x) = g(−5) = 400

b) min f(x) = f(√2) = −3; max f(x) = f(2) = f(0) = 1

c) min f(x) = f(1) = 4. Không có giá trị lớn nhất.

Giải Bài 8 trang 217 SBT toán 12 tập 1

Cho hàm số:

(m là tham số) (1)

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1) khi m = 0.

b) Viết phương trình của tiếp tuyến với đồ thị (C) tại điểm A(0; 9/2)

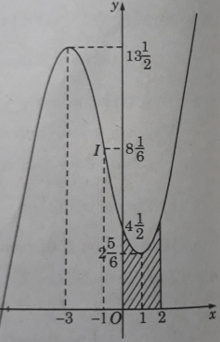
c) Tính diện tích hình phẳng giới hạn bởi (C) , trục hoành và các đường thẳng x = 0 và x = 2.

d) Xác định m để đồ thị của (1) cắt đường thẳng y = −3x + 9/2 tại ba điểm phân biệt.

Lời giải:

    +) Tập xác định: D = R

    +) Sự biến thiên: y’ = x² + 2x – 3

y' = 0 

Bảng biến thiên:

Hàm số đồng biến trên các khoảng (-∞; -3) và (1; +∞), nghịch biến trên khoảng (-3; 1).

Hàm số đạt cực đại tại x = −3; y_CD = 27/2; y_CT = 17/6 khi x = 1

Đồ thị cắt trục tung tại điểm (0; 9/2) và có dạng như hình dưới đây.

y′′ = 2x + 2; y′′ = 0 ⇔ x = −1. Vậy là tâm đối xứng của đồ thị.

b) Tiếp tuyến với (C) đi qua A(0; 9/2) có phương trình là: y = f′(0)x + 9/2, trong đó f(x) = x³/3 + x² − 3x + 9/2

Ta có f ’(0) = -3.

Vậy phương trình tiếp tuyến là y = −3x + 9/2

d) Hoành độ giao điểm của đường thẳng y = −3x + 9/2 với đồ thị của (1) thỏa mãn phương trình

Ta có (2) ⇔ x³/3 − (m − 1)x² + mx = 0 (2)

⇔ x[x² − 3(m − 1)x + 3m] = 0

Để (2) có ba nghiệm phân biệt thì phương trình f(x) = x²– 3(m – 1)x + 3m = 0 phải có hai nghiệm phân biệt khác 0, tức là:

Giải Bài 9 trang 217 SBT toán 12 tập 1

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số

b) Từ (C) suy ra đồ thị của hàm số

c) Viết phương trình tiếp tuyến với (C), biết rằng tiếp tuyến đó song song với đường thẳng

Lời giải:

a) 

Tập xác định: D = R \ {−1/2}

Ta có 

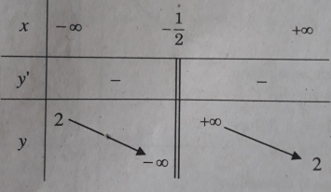
Bảng biến thiên:

Hàm số nghịch biến trên các khoảng (−∞; −1/2) và (−1/2; +∞)

Tiệm cận đứng: x = −1/2;

Tiệm cận ngang: y = 2.

Giao với các trục tọa độ: (0; 4) và (-1; 0)

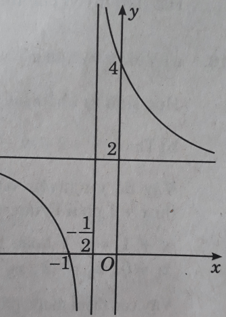
Đồ thị:

b) Đồ thị của hàm số được suy ra từ (C) bằng cách giữ nguyên phần đồ thị nằm phía trên trục hoành và lấy đối xứng qua trục hoành phần đồ thị nằm phía dưới trục hoành (H.6).

c) Tiếp tuyến có hệ số góc bằng −1/4.

Hoành độ tiếp điểm phải thỏa mãn phương trình

⇔ (2x + 1)² = 16

Hai tiếp tuyến cần tìm là

Giải Bài 10 trang 217 SBT toán 12 tập 1

Cho hàm số:

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m = 2.

b) Xác định các điểm có tọa độ nguyên trên đồ thị của (1) khi m ∈ Z.

Lời giải:

a) Với m = 2, ta có: 

Đồ thị:

b) Ta có: 

Vậy để y nguyên với x và m nguyên thì x + 1 phải là ước của 3, tức là: x + 1 = 1 hay x + 1 = -1 hoặc x + 1 = 3 hay x + 1 = -3

x₁ = 0; x₂ = −2; x₃ = −4; x₄ = 2.

Vậy các điểm thuộc đồ thị của (1) có tọa độ nguyên là A(0; m - 1) ; B(-2; 5 + m); C(-4; 3 + m); D(2; m + 1).

Giải Bài 11 trang 217 SBT toán 12 tập 1

Cho a, b, x là những số dương. Đơn giản các biểu thức sau:

a) 

b) 

Lời giải:

Do a, b, x là những số dương nên ta có:

a) A = 3√b

b) Ta có:

 

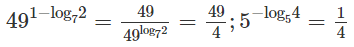
Giải Bài 12 trang 218 SBT toán 12 tập 1

Hãy biểu diễn:

a) log₃₀8 qua a = log₃₀3 và b = log₃₀5;

b) log₉20 qua a = log2 và b = log3.

Lời giải:

a) Ta có

log₃₀8 = log₃₀2³

= 3log₃₀2

= 3.log₃₀(30/15)

= 3(log₃₀30 − log₃₀(3.5))

= 3(1 − log₃₀3 − log₃₀5) = 3(1 – a – b)

b) Chuyển sang cơ số 10.

Sau khi biến đổi, ta được 

Giải Bài 13 trang 218 SBT toán 12 tập 1

Giải các phương trình sau:

 

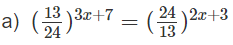
Lời giải:

a) Phương trình đã cho tương đương với

⇔ 3x + 7 = –2x – 3 ⇔ x = –2

b) Vì (4 − √(15))(4 + √(15)) = 1 nên ta đặt (4 − √(15))^tanx = t (t > 0), ta được phương trình

t² − 8t + 1 = 0 

+) Ứng với t = 4 − √(15), ta có

(4 − √(15))^tanx = 4 − √(15)

+) Ứng với t = 4 + √(15), ta có

(4 - √(15))^tanx = 4 + √(15)

Vậy phương trình có nghiệm

c) Ta nhận thấy x = 3 là nghiệm của phương trình. Mặt khác, hàm số

Là tổng của hai hàm số mũ với cơ số lớn hơn 1 (hai hàm số đồng biến) nên f(x) đồng biến trên R. Do đó, x = 3 là nghiệm duy nhất của phương trình.

Giải Bài 14 trang 218 SBT toán 12 tập 1

Giải các phương trình sau:

 

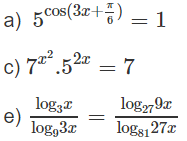
Lời giải:

a) Vì 1 = 5^o nên ta có

 

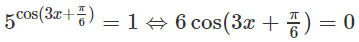
b) 6.4^x − 13.6^x + 6.9^x = 0 (1)

Vì 4^x, 6^x, 9^x đều khác 0 với mọi x ∞ R nên chia cả hai vế của phương trình (1) cho 4^x hoặc 6^x hoặc 9^x , ta được phương trình tương đương.

Chia cả hai vế cho 6^x, ta có: (1)

Đặt 

Ta có:

  

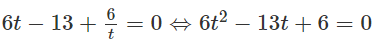
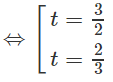
c) Logarit hóa hai vế theo cơ số 7, ta được:

x² + 2x.log₇ 5 − 1 = 0

d) log₄(x + 2).log_x2 = 1

Điều kiện:

 

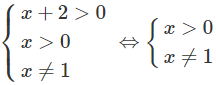
Vậy nghiệm của phương trình là x = 2.

e) Điều kiện: x > 0

Đổi sang cơ số 3 và đặt log₃x = t,

ta được phương trình:

Giải phương trình ẩn t, ta được t₁ = 1, t₂ = −4

Vậy phương trình có hai nghiệm x₁ = 3; x₂ = 1/81

g) Điều kiện:

Đặt log₃x + log₄(2x − 2) = f(x)

Dễ thấy f(x) là hàm số đồng biến. Mặt khác f(3) = 2 nên ta có:

f(x) > f(3) = 2 với x > 3 và f(x) < f(3) = 2 với 1 < x < 3.

Từ đó suy ra x = 3 là nghiệm duy nhất.

Giải Bài 15 trang 218 SBT toán 12 tập 1

Giải các bất phương trình sau:

Lời giải:

a) Điều kiện 

Vì 0 < 0,5 < 1 và 1 = (0,5)⁰ nên ta có:

⇔ log_1/3(x² − 3x + 1) > 0

⇔ x² − 3x + 1 > 1 ⇔ 0 < x < 3

Kết hợp với điều kiện, ta được nghiệm của bất phương trình đã cho là

b) Ta có bất phương trình đã cho tương đương với

4x² + 3.3^√x + x.3^√x − 2x².3^√x − 2x − 6 < 0

⇔ (3 + x − 2x²)3^√x − 2(x − 2x² + 3) < 0

⇔(−2x² + x + 3)(3^√x − 2) < 0

  

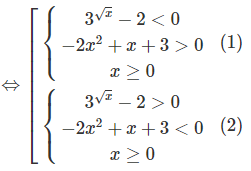
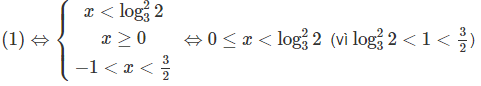
Vậy nghiệm của bất phương trình là x > 3/2 hoặc

Giải Bài 16 trang 218 SBT toán 12 tập 1

a) 

b) 

Lời giải:

a) Bất phương trình đã cho tương đương với

b) Bất phương trình đã cho tương đương với

Ở đây, chúng ta đã áp dụng tính đồng biến và nghịch biến của các hàm số logarit và hàm số mũ với cơ số lớn hơn 1 và nhỏ hơn 1.

Giải Bài 17 trang 218 SBT toán 12 tập 1

Tính các tích phân sau:

a) 

b) 

c) 

d) 

e) 

Lời giải:

a) Đáp số: 

b) Đáp số: 

c) Đáp số:

hoặc

d) Đáp án: 

e) Đáp án: 

Giải Bài 18 trang 219 SBT toán 12 tập 1

Lời giải:

a) Đáp số: 

b) Đáp số: 

c) Đáp số: 

d) Đổi biến 

Đáp án: 

e) 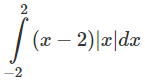 = -8

g)

h) Ta có:

1 + sin2x + cos2x

= 1 + 2sinxcosx + 2cos²x – 1

= 2cosx(sinx + cosx)

Từ đó, ta có đáp số là 1.

i) Áp dụng phương pháp tính tích phân từng phần hai lần, cả hai lần đều đặt e^xdx = dv ⇔ v = e^x

Đáp số: 

Giải Bài 19 trang 219 SBT toán 12 tập 1

Tính diện tích của hình phẳng giới hạn bởi các đường sau:

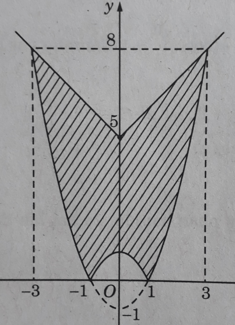
a) y = |x2 – 1| và y = 5 + |x|

b) 2y = x² + x – 6 và 2y = -x² + 3x + 6

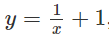
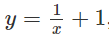
c)  ,x=1 và tiếp tuyến với đường  tại điểm (2; 3/2)

Lời giải:

a) Hai hàm số y = |x2 – 1| và y = 5 + |x| đều là hàm số chẵn. Miền cần tính diện tích được thể hiện ở Hình 8. Do tính đối xứng qua trục tung, ta có:

b) Miền cần tính diện tích được thể hiện bởi Hình 9 (học sinh tự làm)

Như vậy, với mọi x ∈ (-2;3) đồ thị của hàm số

nằm phía trên đồ thị của hàm số

Vậy ta có:

c) Miền cần tính diện tích được thể hiện trên Hình 10:

(vì tiếp tuyến với đồ thị của 

tại điểm (2;3/2) có phương trình là

Giải Bài 20 trang 219 SBT toán 12 tập 1

Tính thể tích của vật thể tròn xoay khi quay các hình phẳng giới hạn bởi các đường sau quanh trục Ox:

a) y = x³; y = 1 và x = 3;

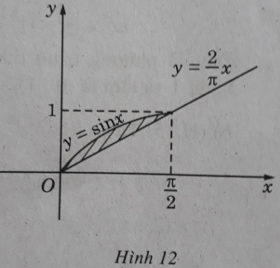
b) y = 2x/π; y = sinx; x ∈ [0; π/2];

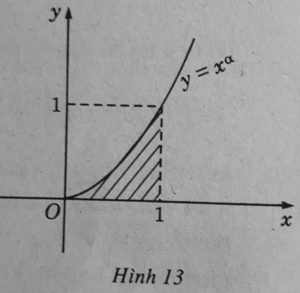
c) y = x^α, α ∈ N^∗; y = 0; x = 0.

Lời giải:

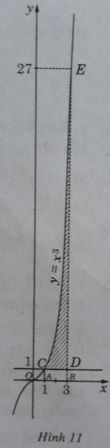
a)(H.11) Thể tích vật thể tròn xoay sinh ra bởi miền CED quay quanh trục Ox là hiệu của hai thể tích (V₁ và V₂) của hai vật thể tròn xoay tương ứng sinh ra khi miền ACEB và miền ACDB quay quanh trục Ox. Như vậy V = V₁ – V₂, trong đó :

b) (H.12) Ta có V = V₁ – V₂ trong đó

c) (H.13)

Giải Bài 21 trang 219 SBT toán 12 tập 1

Chứng minh rằng:

a) i + i² + i³ + ... + i⁹⁹ + i¹⁰⁰ = 0

b) 

Lời giải:

a) Biến đổi vế trái bằng cách nhóm từng bốn số hạng và đặt thừa số chung, ta được

i(1 + i + i² + i³) + ... + i⁹⁷ (1 + i + i² + i³)

= (1 + i + i² + i³)(i + ... + i⁹⁷) = 0

Vì 1 + i + i² + i³ = 1 + i – 1 – i = 0

b) Ta có

= −(2√2i + 2i²) = 2 − 2√2i

Giải Bài 22 trang 219 SBT toán 12 tập 1

Tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa mãn các điều kiện:

a) |z – i| = 1

b) |2 + z| < |2 – z|

c) 2 ≤ |z − 1 + 2i| < 3

Lời giải:

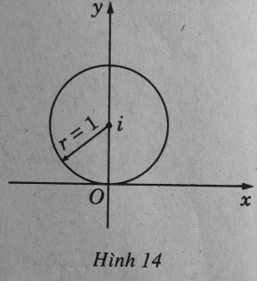
a) Vế trái là khoảng cách từ điểm biểu diễn z dến điểm biểu diễn z₀ = 0 + i . Vậy tập hợp các điểm thỏa mãn điều kiện đã cho là tất cả các điểm cách điểm (0; 1) một khoảng không đổi bằng 1. Đó là các điểm nằm trên đường tròn bán kính bằng 1 và tâm là điểm (0; 1) (H. 14)

Ta có thể tiến hành như sau:

 

Cho z = x + iy, ta có |z − i|² = |x + (y − 1)i|² = x² + (y − 1)² và như vậy ta có: x² + (y − 1)² = 1

Đây là phương trình đường tròn bán kính bằng 1 và tâm là (0; 1)

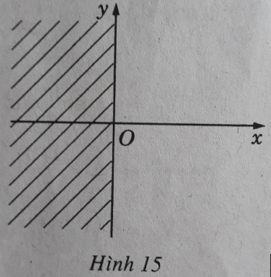
b) (H.15) Ta có: |2 + z|² < |2 − z|²

⇔ |(2 + x) +iy|² < |(2 − x) −iy|²

⇔ (2 + x)² + y² < (2 − x)² + (−y)²

⇔ x < 0

Đó là tập hợp các số phức có phần thực nhỏ hơn 0, tức là nửa trái của mặt phẳng tọa độ không kể trục Oy.

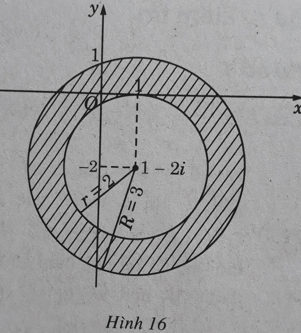
c) Đó là những điểm nằm phía trong hình tròn bán kính bằng 3 và phía ngoài (kể cả biên) hình tròn bán kính bằng 2 có cùng tâm là điểm biểu diễn số phức z₀ = 1 – 2i , tức là những điểm nằm trong hình vành khăn kể cả biên trong. Đó là những điểm (x; y) trên mặt phẳng tọa độ thỏa mãn điều kiện: 4 ≤ (x − 1)² + (y + 2)² < 9

Giải Bài 23 trang 220 SBT toán 12 tập 1

Tính:

Lời giải:

= −1 − 3i + (25 − 10i − 1) = 23 − 13i

Giải Bài 24 trang 220 SBT toán 12 tập 1

Giải các phương trình sau trên tập số phức:

a) 3x² – 4x + 2 = 0

b) x² – x + 9 = 0

Lời giải:

Giải Bài 25 trang 220 SBT toán 12 tập 1

Giải hệ phương trình sau:

Lời giải:

Hệ phương trình tương ứng với:

Vậy nghiệm của hệ là (1 – i , i)

Giải Bài 26 trang 220 SBT toán 12 tập 1

Với những giá trị thực nào của x và y thì các số phức: z₁ = 9y² – 4 – 10xi⁵ và z₂ = 8y² + 20i¹¹ là liên hợp của nhau?

Lời giải:

Để z₁ = z−₂ ta có:

Vậy có hai cặp (x; y) là (-2; 2) và (-2; -2).

Giải Bài 27 trang 220 SBT toán 12 tập 1

Tìm môđun của các số phức sau:

a) z₁ = −8 + 0,5i

b) z₂ = √3 − √7i

Lời giải:

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về giải bài tập SBT toán lớp 12 tập 2 Ôn tập cuối năm, file PDF hoàn toàn miễn phí.