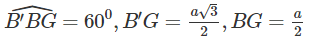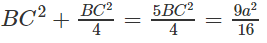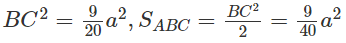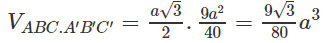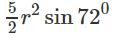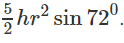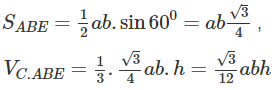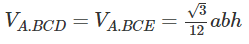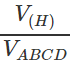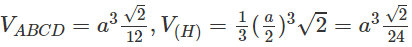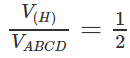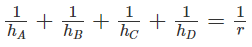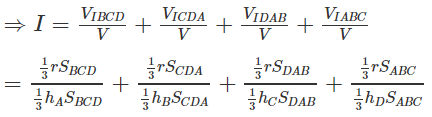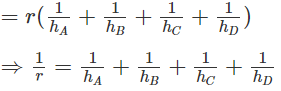Giải SBT Toán Hình học 12 trang 20 tập 1 Đề toán tổng hợp chương 1 đầy đủ

Với bộ tài liệu giải sách bài tập toán Hình học 12 tập 1 Đề toán tổng hợp chương 1, hướng dẫn cách giải chi tiết cho từng câu hỏi, từng phần học bám sát nội dung chương trình SBT bộ môn Toán lớp 12. Nội dung chi tiết các em xem tại đây.

Giải Bài 1.28 trang 20 SBT toán 12 tập 1

Hình được tạo thành từ hình lập phương ABCD.A’B’C’D’ khi ta bỏ đi các điểm trong của mặt phẳng (ABCD) có phải là một hình đa diện không?

Lời giải:

Không phải là hình đa diện, vì trong hình đó có cạnh (chẳng hạn AB) không phải là cạnh chung của đúng hai đa giác.

Giải Bài 1.29 trang 20 SBT toán 12 tập 1

Chứng minh rằng mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất ba cạnh.

Lời giải:

Lấy một đỉnh B tùy ý của hình đa diện (H). Gọi M₁ là một mặt của hình đa diện (H) chứa B. Gọi A, B, C là ba đỉnh liên tiếp của M₁. Khi đó AB, BC là hai cạnh của (H). Gọi M₂ là mặt khác với M₁ và có chung cạnh AB với M₁. Khi đó M₂ còn có ít nhất một đỉnh D sao cho A, B, D là ba đỉnh khác nhau liên tiếp của M₂. Nếu D ≡ C thì ₁ và M₂ có hai cạnh chung AB và BC, điều này vô lí. Vậy D phải khác C. Do đó qua đỉnh B có ít nhất ba cạnh BA, BC và BD.

Giải Bài 1.30 trang 20 SBT toán 12 tập 1

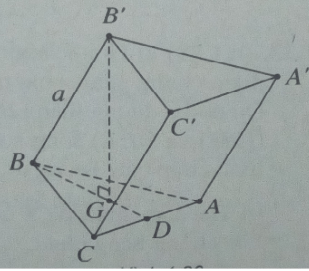
Cho hình lăng trị ABC.A’B’C’ có đáy là tam giác vuông cân ở C. Cạnh B’B = a và tạo với đáy một góc bằng 60^o. Hình chiếu vuông góc hạ từ B’ lên đáy trùng với trọng tâm của tam giác ABC. Tính thể tích khối lăng trụ đó theo a.

Lời giải:

Gọi G là trọng tâm của tam giác ABC, khi đó

Gọi D là trung điểm của AC, khi đó BD = 3a/4.

Ta có BC² + CD² = BD²

do đó 

Suy ra

Giải Bài 1.31 trang 20 SBT toán 12 tập 1

Tính thể tích khối lăng trụ có chiều cao bằng h, đáy là ngũ giác đều nội tiếp trong một đường tròn bán kính r.

Lời giải:

Chia đáy của hình lăng trụ đã cho thành năm tam giác cân có chung đỉnh O là tâm đường tròn ngoại tiếp đáy.

Khi đó diện tích đáy bằng: 

Do đó thể tích lăng trụ đó bằng: 

Giải Bài 1.32 trang 20 SBT toán 12 tập 1

Cho hai đoạn thẳng AB và CD chéo nhau, AC là đường vuông góc chung của chúng. Biết rằng AC = h, AB = a, CD = b và góc giữa hai đường thẳng AB và CD bằng 600. Hãy tính thể tích của khối tứ diện ABCD.

Lời giải:

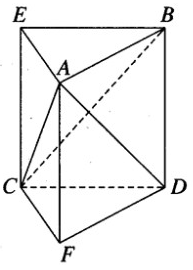
Dựng BE song song và bằng DC, DF song song và bằng BA. Khi đó, ABE.FDC là một lăng trụ đứng.

Ta có:

Giải Bài 1.33 trang 20 SBT toán 12 tập 1

Cho tứ diện đều ABCD. Gọi (H) là hình bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện đều đó. Tính tỉ số:

Lời giải:

Gọi cạnh của tứ diện đều ABCD là a thì cạnh của hình bát diện đều (H) là a/2. Khi đó

Từ đó suy ra 

Giải Bài 1.34 trang 20 SBT toán 12 tập 1

 

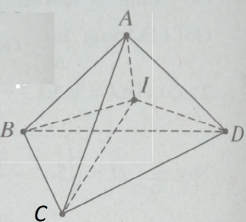
Cho tứ diện ABCD. Gọi h_A, h_B, h_C, h_D lần lượt là các đường cao của tứ diện xuất phát từ A, B, C, D và r là bán kính mặt cầu nội tiếp tứ diện. Chứng minh rằng:

Lời giải:

V = V_IBCD + V_ICDA + V_IDAB + V_IABC

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về giải SBT toán hình lớp 12 tập 1 Đề toán tổng hợp chương 1, file PDF hoàn toàn miễn phí.