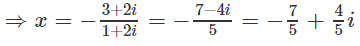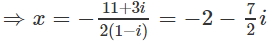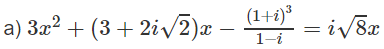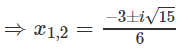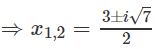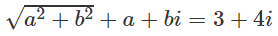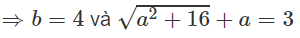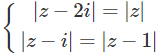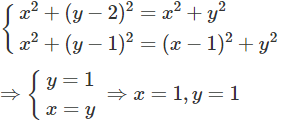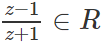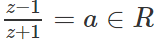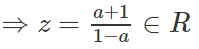Giải SBT Toán 12 trang 207, 208 tập 2 Bài tập ôn tập chương 4 đầy đủ

Với bộ tài liệu giải sách bài tập toán 12 tập 2 Bài tập ôn tập chương 4, hướng dẫn cách giải chi tiết cho từng câu hỏi, từng phần học bám sát nội dung chương trình SBT bộ môn Toán lớp 12. Nội dung chi tiết các em xem tại đây.

Giải Bài 4.35 trang 207 SBT toán 12 tập 1

Áp dụng các hằng đẳng thức đáng nhớ để tính:

a) (2 + i√3)²;

b) (1 + 2i)³;

c) (3 − i√2)²;

d) (2 − i)³.

Lời giải:

a) 1 + 4i√3;

b) – 11 – 2i;

c) 7 − 6i√2;

d) 2 – 11i.

Giải Bài 4.36 trang 207 SBT toán 12 tập 1

Giải các phương trình sau trên tập số phức:

a) (1 + 2i)x – (4 – 5i) = –7 + 3i

b) (3 + 2i)x – 6ix = (1 – 2i)[x – (1 + 5i)]

Lời giải:

a) (1 + 2i)x = − 3 −2i

b) (2 − 2i)x = −(11 + 3i)

Giải Bài 4.37 trang 208 SBT toán 12 tập 1

Giải các phương trình sau trên tập số phức:

b) (1 − ix)² + (3 + 2i)x − 5 = 0

Lời giải:

a) 3x² + 3x + 2 = 0

b) −x² + 3x − 4 = 0

Giải Bài 4.38 trang 208 SBT toán 12 tập 1

Tìm số phức z, biết:

a) z− = z³;

b) |z| + z = 3 + 4i.

Lời giải:

a) Ta có zz− = |z|² nên từ z− = z³ ⇒ |z|² = z⁴

Đặt z = a+ bi , suy ra:

a⁴ + b⁴ − 6a²b² + 4ab(a² − b²)i = a² + b² (∗)

Do đó, ta có: 4ab(a² − b²) = 0 (∗∗)

Từ (∗∗) suy ra các trường hợp sau:

     +) a = b = 0 ⇒ z = 0

     +) a = 0, b ≠ 0: Thay vào (∗), ta có b⁴ = b² ⇒ b = 1 hoặc b = -1 ⇒ z = i hoặc z = -1

     +) b = 0, a ≠ 0: Tương tự, ta có a = 1 hoặc a = -1 ⇒ z = 1 hoặc z = -1

     +) a ≠ 0, b ≠ 0 ⇒ a² − b² = 0⇒ a² = b², thay vào (∗) , ta có:

2a²(2a² + 1) = 0, không có a nào thỏa mãn (vì a ≠ 0 )

b) Đặt z = a + bi. Từ |z| + z = 3 + 4i suy ra

⇒ a² + 16 = (3 − a)² = 9 − 6a + a²

⇒ 6a = −7 ⇒ a = −7/6

Vậy z = −7/6 + 4i

Giải Bài 4.39 trang 208 SBT toán 12 tập 1

Tìm số phức z thỏa mãn hệ phương trình:

Lời giải:

Đặt z = x + yi , ta được hệ phương trình:

Vậy z = 1 + i.

Giải Bài 4.40 trang 208 SBT toán 12 tập 1

Chứng tỏ rằng 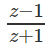 là số thực khi và chỉ khi z là một số thực khác – 1.

Lời giải:

Hiển nhiên nếu z ∈ R, z ≠ −1 thì 

Ngược lại, nếu 

thì z – 1 = az + a và a ≠ 1

Suy ra (1 − a)z = a + 1

và hiển nhiên z ≠ −1.

Giải Bài 4.41 trang 208 SBT toán 12 tập 1

Tìm phần ảo của số phức z , biết z− = (√2 + i)²(1 − i√2)

(Đề thi đại học năm 2010, khối A)

Lời giải:

z− = (√2 + i)² (1 − i√2)

= (2 + 2√2i + i²) (1 − i√2)

= (1 + 2√2) (1 − i√2)

= 1 − √2i + 2√2i − 4i²

= 5 + √2i

⇒ z = 5 −√2i

Phân ảo của số phức z = −√2

Giải Bài 4.42 trang 208 SBT toán 12 tập 1

Trên mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn |z – (3 – 4i)|=2

(Đề thi Đại học năm 2009, khối D)

Lời giải:

Đặt z = x + yi. Từ |z – (3 – 4i)| = 2 suy ra:

(x − 3)² + (y + 4)² = 4

Các điểm biểu diễn z nằm trên đường tròn tâm I(3; -4) bán kính 2.

Giải Bài 4.43 trang 208 SBT toán 12 tập 1

Trên mặt phẳng Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện |z – i| = |(1 + i)z|.

(Đề thi Đại học năm 2010, khối B)

Lời giải:

Đặt z = x + yi. Từ |z – i| = |(1 + i)z| suy ra :

x² + (y + 1)² = 2

Các điểm biểu diễn z nằm trên đường tròn tâm I(0; -1) bán kính

Giải Bài 4.44 trang 208 SBT toán 12 tập 1

Tìm số phức z thỏa mãn:

|z − (2 + i)| = √10 và z−z = 25

Lời giải:

Đặt z = x + yi. Từ điều kiện của đầu bài ta được:

(x – 2)² + (y – 1)² = 10 và x² + y² = 25

Đáp số: z = 5 và z = 3 + 4i

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về giải SBT toán lớp 12 tập 2 Bài tập ôn tập chương 4, file PDF hoàn toàn miễn phí.