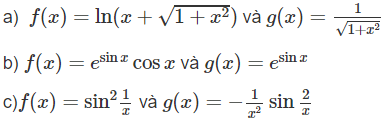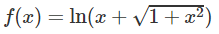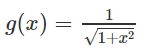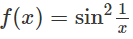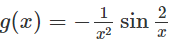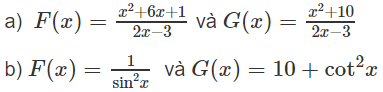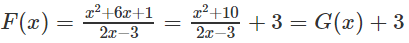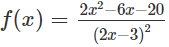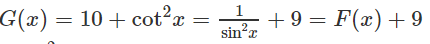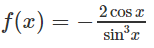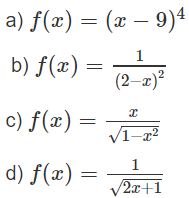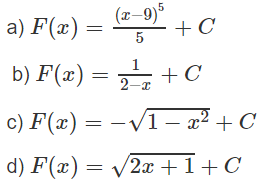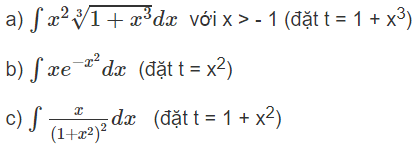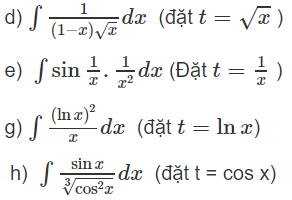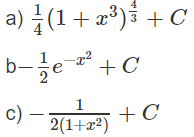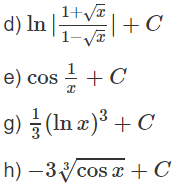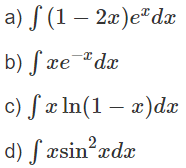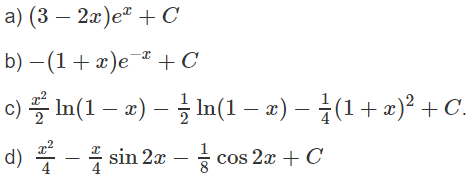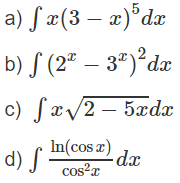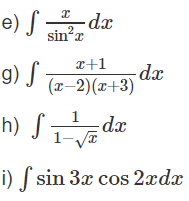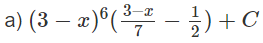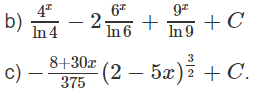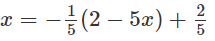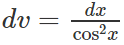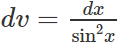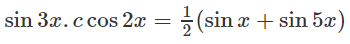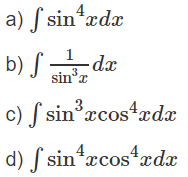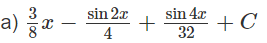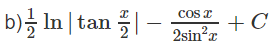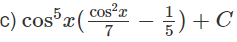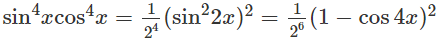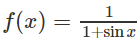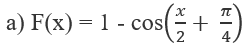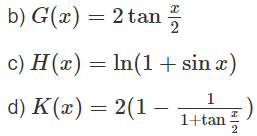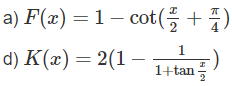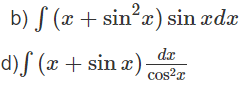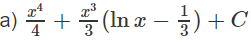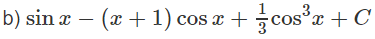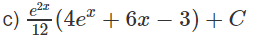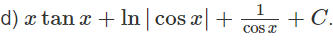Giải SBT toán 12 trang 163, 164, 165 tập 2 Bài 1 đầy đủ

Với bộ tài liệu giải sách bài tập toán 12 tập 2 Bài 1: Nguyên hàm, hướng dẫn cách giải chi tiết cho từng câu hỏi, từng phần học bám sát nội dung chương trình SBT bộ môn Toán lớp 12. Nội dung chi tiết các em xem tại đây.

Giải Bài 3.1 trang 163 SBT toán 12 tập 2

Kiểm tra xem nguyên hàm nào là một nguyên hàm của hàm số còn lại trong mỗi cặp hàm số sau:

Lời giải:

a) Hàm số 

là một nguyên hàm của 

b) Hàm số g(x) = e^sinx là một nguyên hàm của hàm số f(x) = e^sinx.cosx

c) Hàm số 

là một nguyên hàm của hàm số 

Giải Bài 3.2 trang 163 SBT toán 12 tập 2

Chứng minh rằng các hàm số F(x) và G(x) sau đều là một nguyên hàm của cùng một hàm số:

Lời giải:

a) Vì

nên F(x) và G(x) đều là một nguyên hàm của

b) Vì

nên F(x) và G(x) đều là một nguyên hàm của

Giải Bài 3.3 trang 164 SBT toán 12 tập 2

Lời giải:

Giải Bài 3.4 trang 164 SBT toán 12 tập 2

Tính các nguyên hàm sau bằng phương pháp đổi biến số:

 

Lời giải:

 

Giải Bài 3.5 trang 164 SBT toán 12 tập 2

Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính:

Lời giải:

HD: Đặt u = x, dv = sin²xdx

Giải Bài 3.6 trang 164 SBT toán 12 tập 2

 

Lời giải:

Hướng dẫn: Đặt t = 3 - x

Hướng dẫn: Dựa vào 

d) tanx[ln(cosx) + 1] – x + C.

Hướng dẫn: Đặt u = ln(cosx), 

e) −xcotx + ln|sinx| + C.

Hướng dẫn: Đặt u = x, 

Hướng dẫn: Ta có:

h) −2(√x + ln|1 − √x|) + C

Hướng dẫn: Đặt t = √x

Hướng dẫn:

Giải Bài 3.7 trang 164 SBT toán 12 tập 2

Bằng cách biến đổi các hàm số lượng giác, hãy tính:

Lời giải:

Hướng dẫn:

 

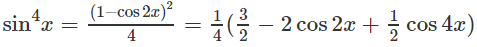
Hướng dẫn: Đặt u = cosx

Hướng dẫn: Đặt u = cosx

Hướng dẫn:

Giải Bài 3.8 trang 165 SBT toán 12 tập 2

Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số

Lời giải:

Giải Bài 3.9 trang 165 SBT toán 12 tập 2​​​​​​​

Tính các nguyên hàm sau đây:

 

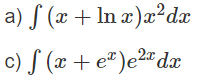
Lời giải:

Hướng dẫn: Đặt u = x + lnx; dv = x²dx

Hướng dẫn: Đặt u = x + sin²x, dv = sinxdx

Hướng dẫn: Đặt u = x + e^x, dv = e^2xdx

Hướng dẫn: Đặt u = x + sinx, dv = d(tanx)

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về giải bài tập SBT toán 12 tập 1 Bài 1: Nguyên hàm, file PDF hoàn toàn miễn phí.