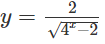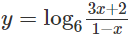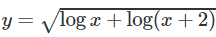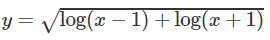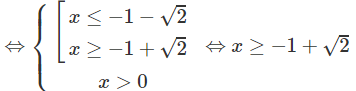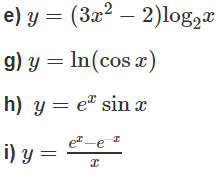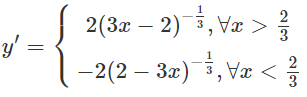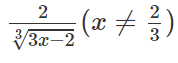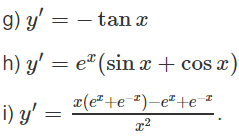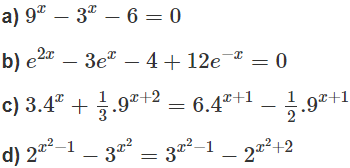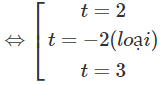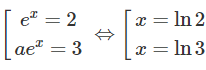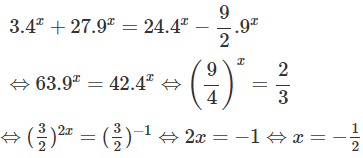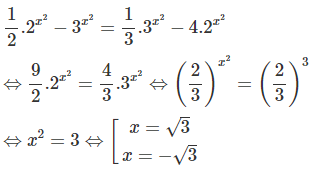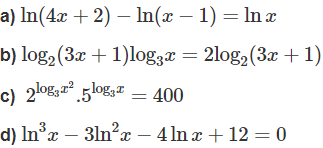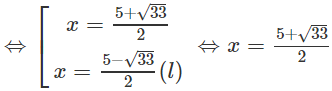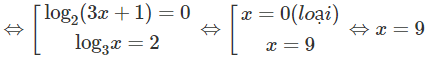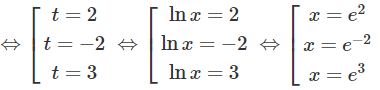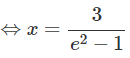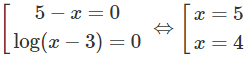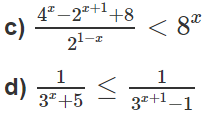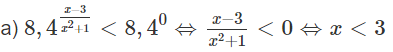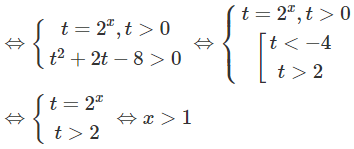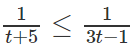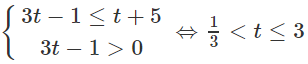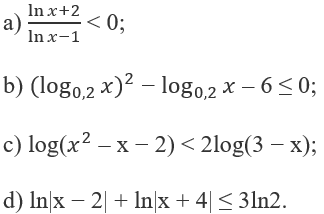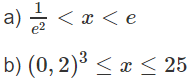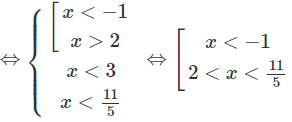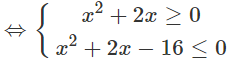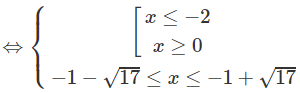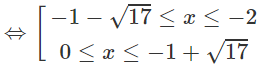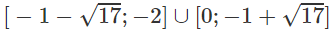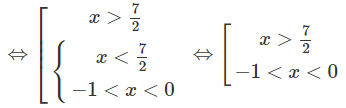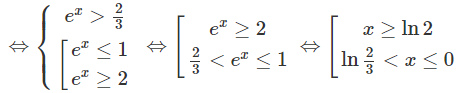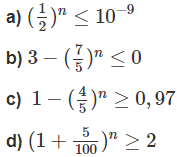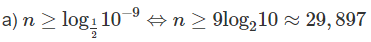Giải SBT toán 12 trang 133, 134 tập 1 Bài tập ôn tập chương 2 đầy đủ

Với bộ tài liệu giải sách bài tập toán 12 tập 1 Bài tập ôn tập chương 2, hướng dẫn cách giải chi tiết cho từng câu hỏi, từng phần học bám sát nội dung chương trình SBT bộ môn Toán lớp 12. Nội dung chi tiết các em xem tại đây.

Giải Bài 2.65 trang 133 SBT toán 12 tập 1

Tìm tập xác định của các hàm số sau:

a) 

b) 

c) 

d) 

Lời giải:

a) Hàm số xác định khi:

4^x – 2 > 0 ⇔ 2^2x > 2 ⇔ x > 1/2

Vậy tập xác định là D = (1/2; +∞)

b) D = (−2/3; 1)

c) logx + log(x + 2) ≥ 0

 

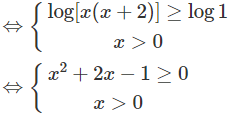
Vậy tập xác định là D = [−1 + √2; +∞)

d) Tương tự câu c, D = [√2; +∞).

Giải Bài 2.66 trang 133 SBT toán 12 tập 1

Tính đạo hàm của các hàm số sau:

 

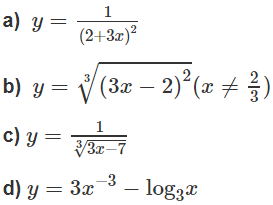
Lời giải:

a) y′ = −6(2 + 3x)⁻³

b)

y' = 

 

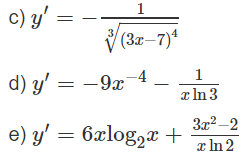
Giải Bài 2.67 trang 133 SBT toán 12 tập 1

Giải các phương trình sau:

Lời giải:

a) x = 1

b) Đặt t = e^x (t > 0), ta có phương trình t² − 3t – 4 + 12/t = 0 hay

t³ − 3t² − 4t + 12 = 0

⇔ (t − 2)(t + 2)(t − 3) = 0

Do đó

c)

d)

Giải Bài 2.68 trang 133 SBT toán 12 tập 1

Giải các phương trình sau:

Lời giải:

a) Với điều kiện x > 1 ta có phương trình:

ln(4x + 2) = ln[x(x − 1)]

⇔ 4x + 2 = x² – x ⇔ x² – 5x – 2 = 0

b) Với điều kiện x > 0, ta có phương trình

log₂(3x + 1)[log₃x − 2] = 0

c) Với điều kiện x > 0, ta có phương trình:

4^log₃x. 5^log₃x = 400

⇔ 20^log₃x = 20²

⇔ log₃x = 2 ⇔ x = 9 (thỏa mãn điều kiện)

d) Đặt t = lnx(x > 0), ta có phương trình:

t³ – 3t² – 4t + 12 = 0 ⇔ (t – 2)(t + 2)(t – 3) = 0

Giải Bài 2.69 trang 133 SBT toán 12 tập 1

Giải các phương trình sau:

a) e^2+lnx = x + 3;

b) e^4−lnx = x;

c) (5 − x).log(x − 3) = 0

Lời giải:

a) Với điều kiện x > 0, ta có phương trình

e². e^lnx = x + 3

⇔ e².x = x + 3

⇔x(e² − 1) = 3

(thỏa mãn điều kiện)

b) Tương tự câu a), x = e²

c) Với điều kiện x > 3 ta có:

Giải Bài 2.70 trang 133 SBT toán 12 tập 1

Giải các bất phương trình mũ sau:

 

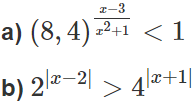
Lời giải:

b) 2^{|x − 2|} > 2^2|x+1|

⇔ |x−2| > 2|x+1|

⇔ x² − 4x + 4 > 4(x² + 2x + 1)

⇔ 3x² + 12x < 0

⇔ −4 < x < 0

c) 2^2x − 2.2^x + 8 < 2^3x. 2^1−x

⇔ 2^2x + 2.2^x − 8 > 0

d) Đặt t = 3^x (t > 0) , ta có bất phương trình

Vì vế trái dương nên vế phải cũng phải dương, tức là 3t - 1 > 0.

Từ đó ta có hệ:

Do đó 1/3 < 3x ≤ 3. Vậy −1 < x ≤ 1.

Giải Bài 2.71 trang 134 SBT toán 12 tập 1

Giải các bất phương trình lôgarit sau:

Lời giải:

c) Bất phương trình đã cho tương đương với hệ:

 

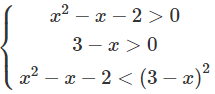
Vậy tập nghiệm là (−∞; −1) ∪ (2; 11/5)

d) ln|(x − 2)(x + 4)| ≤ ln8

⇔|x² + 2x − 8| ≤ 8

⇔ −8 ≤ x² + 2x – 8 ≤ 8

Vậy tập nghiệm là

Giải Bài 2.72 trang 134 SBT toán 12 tập 1

Giải các bất phương trình sau:

a) (2x − 7)ln(x + 1) > 0;

b) (x − 5)(logx + 1) < 0;

c) 2log₃²x + 5log₂² + log₂x – 2 ≥ 0

d) ln(3e^x − 2) ≤ 2x

Lời giải:

a) Bất phương trình đã cho tương đương với hệ sau:

 

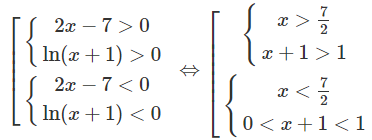
Vậy tập nghiệm là (−1;0) ∪ (7/2; +∞)

b) Tươngg tự câu a), tập nghiệm là (1/10; 5)

c) Đặt t = log₂x, ta có bất phương trình 2t³ + 5t² + t – 2 ≥ 0 hay (t + 2)(2t² + t − 1) ≥ 0 có nghiệm −2 ≤ t ≤ −1 hoặc t ≥ 1/2

Suy ra 1/4 ≤ x ≤ 1/2 hoặc x ≥ √2

Vậy tập nghiệm của bất phương trình đã cho là: [1/4; 1/2] ∪ [√2; +∞)

d) Bất phương trình đã cho tương đương với hệ:

 

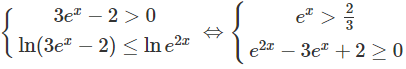
Vậy tập nghiệm là (ln(2/3); 0] ∪ [ln2; +∞)

Giải Bài 2.73 trang 134 SBT toán 12 tập 1

 

Tìm số tự nhiên n bé nhất sao cho:

Lời giải:

Vì n là số tự nhiên bé nhất nên n = 30.

b) n = 4

c) n = 16

d) n = 15

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về giải SBT toán lớp 12 tập 1 Bài tập ôn tập chương 2, file PDF hoàn toàn miễn phí.