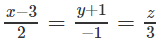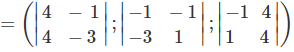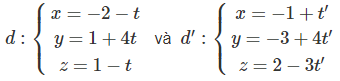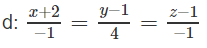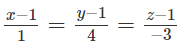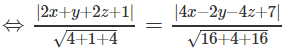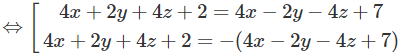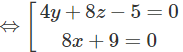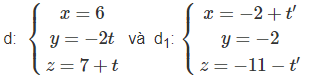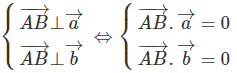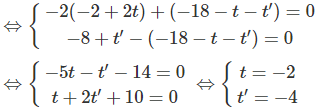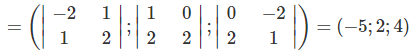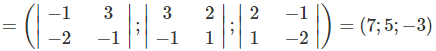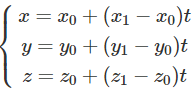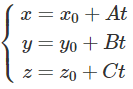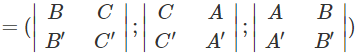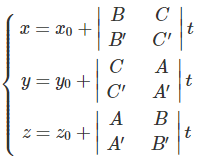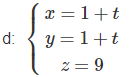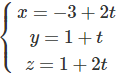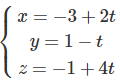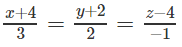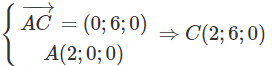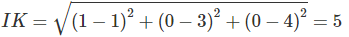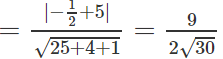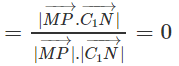Giải SBT Toán Hình học 12 trang 132, 133, 134 tập 2 Câu hỏi và bài tập chương 3

Với bộ tài liệu giải sách bài tập toán Hình học 12 tập 2 Câu hỏi và bài tập chương 3, hướng dẫn cách giải chi tiết cho từng câu hỏi, từng phần học bám sát nội dung chương trình SBT bộ môn Toán lớp 12. Nội dung chi tiết các em xem tại đây.

Giải Bài 3.46 trang 132 SBT toán 12 tập 1

Lập phương trình mặt phẳng (P) đi qua điểm M(1; -3; 2) và vuông góc với đường thẳng d:

Lời giải:

Chọn n_P→ = (2; −1; 3).

Phương trình của (P) là: 2(x – 1) – (y + 3) + 3(z – 2) = 0 hay 2x – y + 3z – 11 = 0.

Giải Bài 3.47 trang 132 SBT toán 12 tập 1

Lập phương trình mặt phẳng (P) đi qua điểm M(1; -3; 2) và song song với mặt phẳng (Q): x – z = 0.

Lời giải:

Chọn n_P→ = n_Q→ = (1; 0; −1)

Phương trình của (P) là: (x – 1) – (z – 2) = 0 hay x – z + 1 = 0.

Giải Bài 3.48 trang 132 SBT toán 12 tập 1

Lập phương trình mặt phẳng (P) đi qua ba điểm A(-1; -3; 2), B(-2; 1; 1) và C(0; 1; -1).

Lời giải:

Ta có: AB→(−1; 4; −1); AC→(1; 4; −3)

⇒ AB→ ∧ AC→ 

= (−8; −4; −8)

Suy ra có thể chọn n_P→ = (2; 1; 2)

Phương trình của (P) là: 2x + (y – 1) + 2(z + 1) = 0 hay 2x + y + 2z + 1 = 0.

Giải Bài 3.49 trang 133 SBT toán 12 tập 1

Lập phương trình mặt phẳng (P) chứa hai đường thẳng:

Lời giải:

Đường thẳng d đi qua M(-2; 1; 1) có vecto chỉ phương là a→(−1; 4; −1)

Đường thẳng d’ đi qua N(-1; -3; 2) có vecto chỉ phương là b→(1; 4; −3)

Suy ra: a→ ∧ b→ = (−8; −4; −8) ≠ 0→

Ta có: MN→(1; −4; 1) nên MN→.(a→ ∧ b→) = 0 do đó hai đường thẳng d và d’ cắt nhau.

Khi đó (P) là mặt phẳng đi qua M(-2; 1; 1) và có n_P→ = (2; 1; 2)

Phương trình của (P) là : 2(x + 2) + (y – 1) + 2(z – 1) = 0 hay 2x + y + 2z + 1 = 0.

Giải Bài 3.50 trang 133 SBT toán 12 tập 1

Lập phương trình mặt phẳng (P) đi qua điểm I(-1; -1; 1) và chứa đường thẳng:

Lời giải:

Đường thẳng d đi qua M(-2; 1; 1) có vecto chỉ phương a→(−1; 4; −1)

Ta có: MI→(1; −2; 0), chọn n^P→ = MI→ ∧ a→ = (2; 1; 2)

Phương trình của (P) là: 2(x + 2) + (y – 1) + 2(z – 1) = 0 hay 2x + y + 2z + 1 = 0

Giải Bài 3.51 trang 133 SBT toán 12 tập 1

Lập phương trình mặt phẳng (P) chứa đường thẳng

d: 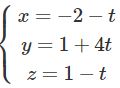 và song song với d₁:

Lời giải:

Đường thẳng d đi qua M(-2; 1; 1) có vecto chỉ phương là a→ (−1; 4; −1)

Đường thẳng d1 đi qua N(1; 1; 1) có vecto chỉ phương là b→ (1; 4; −3)

Ta có: MN→ (3; 0; 0); a→ ∧ b→ = (−8; −4; −8) nên MN→(a→ ∧ b→) ≠ 0, suy ra d và d₁ chéo nhau. Do đó (P) là mặt phẳng đi qua M(-2; 1; 1) có vecto pháp tuyến bằng a→ ∧ b→

Phương trình của (P) là: –8(x + 2) – 4(y – 1) – 8(z – 1) = 0 hay 2x + y + 2z + 1 = 0

Giải Bài 3.52 trang 133 SBT toán 12 tập 1

Lập phương trình mặt phẳng (P) song song và cách đều hai mặt phẳng

(P₁): 2x + y + 2z + 1 = 0 và (P₂): 2x + y + 2z + 5 = 0.

Lời giải:

Ta có: M(x, y, z) ∈ (P)

⇔ d(M, (P₁)) = d(M, (P₂))

⇔|2x + y + 2z + 1| = |2x + y + 2z + 5|

⇔ 2x + y + 2z + 1 = – (2x + y + 2z + 5)

⇔ 2x + y + 2z + 3 = 0

Từ đó suy ra phương trình của (P) là: 2x + y + 2z + 3 = 0.

Giải Bài 3.53 trang 133 SBT toán 12 tập 1

Cho hai mặt phẳng:

(P₁): 2x + y + 2z + 1 = 0 và (P₂): 4x – 2y – 4z + 7 = 0.

Lập phương trình mặt phẳng sao cho khoảng cách từ mỗi điểm của nó đến (P₁) và (P₂) là bằng nhau.

Lời giải:

Ta có: M(x, y, z) ∈ (P) ⇔ d(M, (P₁)) = d(M, (P₂))

⇔ 2|2x + y + 2z + 1| = |4x − 2y − 4z + 7|

Từ đó suy ra phương trình mặt phẳng phải tìm là: 4y + 8z – 5 = 0 hoặc 8x + 9 = 0

Giải Bài 3.54 trang 133 SBT toán 12 tập 1

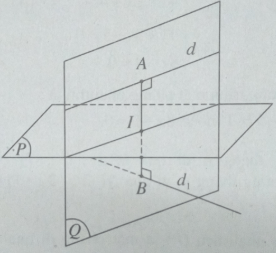
Cho hai đường thẳng:

Lập phương trình mặt phẳng (P) sao cho khoảng cách từ d và d₁ đến (P) là bằng nhau.

Lời giải:

Đường thẳng d đi qua M(6; 0 ;7) có vecto chỉ phương a→(0; −2; 1). Đường thẳng d₁ đi qua N(-2; -2; -11) có vecto chỉ phương b→(1; 0; −1).

Do d và d₁ chéo nhau nên (P) là mặt phẳng đi qua trung điểm của đoạn vuông góc chung AB của d, d₁ và song song với d và d₁.

Để tìm tọa độ của A, B ta làm như sau:

Lấy điểm A(6; - 2t; 7 + t) thuộc d, B( -2 + t’; -2; -11 – t’) thuộc d₁. Khi đó: AB→ = (−8 + t′; −2 + 2t; −18 – t − t′)

Ta có: 

Suy ra A(6; 4; 5), B(-6; -2; -7)

Trung điểm của AB là I(0; 1; -1)

Ta có: AB→ = (−12; −6; −12). Chọn n_P→ = (2; 1; 2)

Phương trình của (P) là: 2x + (y – 1) + 2(z + 1) = 0 hay 2x + y + 2z + 1 = 0.

Có thể tìm tọa độ của A, B bằng cách khác:

Ta có: Vecto chỉ phương của đường vuông góc chung của d và d₁ là:

 = (2; 1; 2)

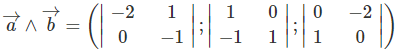
Gọi (Q) là mặt phẳng chứa d và đường vuông góc chung AB.

Khi đó:

n_Q→ = a→ ∧ (a→ ∧ b→)

Phương trình của (Q) là : –5(x – 6) + 2y + 4(z – 7) = 0 hay –5x + 2y + 4z + 2 = 0

Để tìm d₁ ∩ (Q) ta thế phương trình của d₁ vào phương trình của (Q). Ta có:

–5(–2 + t′) + 2(–2) + 4(–11 – t′) + 2 = 0

⇒ t′ = 4

⇒ d₁ ∩ (Q) = B(−6; −2; −7)

Tương tự, gọi (R) là mặt phẳng chứa d₁ và đường vuông góc chung AB. Khi đó: n_R→ = (−1; 4; −1)

Phương trình của (R) là –x + 4y – z – 5 = 0.

Suy ra d ∩ (R) = A(6; 4; 5).

Giải Bài 3.55 trang 133 SBT toán 12 tập 1

Lập phương trình mặt phẳng (P) đi qua điểm M(1; -3; 2) và vuông góc với hai mặt phẳng (Q): 2x – y + 3z + 1 = 0 và (R): x – 2y – z + 8 = 0

Lời giải:

Chọn:

n_P→ = n_Q→ ∧ n_R→

Phương trình của (P) là:

7(x – 1) + 5(y + 3) – 3(z – 2) = 0

Hay 7x + 5y – 3z + 14 = 0

Giải Bài 3.56 trang 133 SBT toán 12 tập 1

Lập phương trình tham số của đường thẳng d đi qua hai điểm phân biệt M₀(x₀; y₀; z₀) và M₁(x₁, y₁, z₁)

Lời giải:

Đường thẳng d đi qua M0 và có vecto chỉ phương M₀M₁→

Do đó phương trình tham số của d là:

Giải Bài 3.57 trang 133 SBT toán 12 tập 1

Lập phương trình tham số của đường thẳng d đi qua điểm M₀(x₀, y₀, z₀) và vuông góc với mặt phẳng (P): Ax + By + Cz + D = 0.

Lời giải:

Đường thẳng d đi qua M0 và có vecto chỉ phương n_P→(A; B; C)

Do đó phương trình tham số của d là:

Giải Bài 3.58 trang 133 SBT toán 12 tập 1

Lập phương trình tham số của đường thẳng d đi qua điểm M₀(x₀, y₀, z₀) và song song với hai mặt phẳng cắt nhau

(P) Ax + By + Cz + D = 0 và (Q): A’x + B’y + C’z + D’ = 0

Lời giải:

Do (P) và (Q) cắt nhau nên n_P→ ∧ n_Q→ ≠ 0→. Đường thẳng d đi qua M₀ và có vecto chỉ phương

 

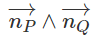
Do đó phương trình tham số của d là:

Đặc biệt phương trình trên cũng là phương trình đường thẳng là giao của hai mặt phẳng cắt nhau (P): Ax + By + Cz + D = 0 và (Q): A’x + B’y + C’z + D’ = 0 với M₀ là điểm chung của (P) và (Q).

Giải Bài 3.59 trang 134 SBT toán 12 tập 1

Cho mặt phẳng (P) : x + 2y – 2z + 3 = 0

và đường thẳng 

Lập phương trình đường thẳng d’ là hình chiếu vuông góc của d lên mặt phẳng (P).

Lời giải:

Đường thẳng d đi qua A(1; 1; 9) và có vecto chỉ phương a→(1; 1; 0). Gọi (Q) là mặt phẳng đi qua d và vuông góc với (P).

Ta có: n_Q→ = a→ ∧ n_P→ = (−2; 2; 1)

Phương trình của (Q) là : -2x + 2y + z – 9 = 0

Khi đó: d′ = (P) ∩ (Q)

Ta có: n_P→ ∧ n_Q→ = (6; 3; 6)

Chọn vecto chỉ phương của d’ là: n_a'→ = (2; 1; 2)

Lấy một điểm thuộc (P) ∩ (Q), chẳng hạn A(-3; 1; 1)

Khi đó, phương trình của d’ là: 

Giải Bài 3.60 trang 134 SBT toán 12 tập 1

Trong không gian Oxyz, cho điểm A(-4; -2; 4) và đường thẳng d:

Viết phương trình đường thẳng Δ đi qua A , cắt và vuông góc với đường thẳng d.

Lời giải:

Ta có: a_d→ = (2; −1; 4)

Xét điểm B(–3 + 2t; 1 – t; –1 + 4t) thì AB→ = (1 + 2t; 3 − t; −5 + 4t)

AB ⊥ d ⇔ AB→.a_d→ = 0

⇔ 2(1 + 2t) − (3 − t) + 4(−5 + 4t) = 0 ⇔ t = 1

Suy ra AB→ = (3; 2; −1)

Vậy phương trình của Δ là 

Giải Bài 3.61 trang 134 SBT toán 12 tập 1

Trong không gian Oxyz, cho hai điểm A(2; 0; 0), B(0; 0; 8) và điểm C sao cho AC→ = (0; 6; 0). Tính khoảng cách từ trung điểm I của BC đến đường thẳng OA.

Lời giải:

Do đó I(1; 3; 4)

Phương trình mặt phẳng (α) qua I và vuông góc với OA là: x – 1 = 0, (α) cắt OA tại K(1; 0; 0)

Khoảng cách từ I đến OA là:

Giải Bài 3.62 trang 134 SBT toán 12 tập 1

 

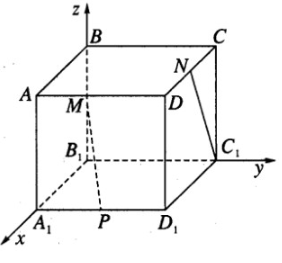
Cho hình lập phương ABCD.A₁B₁C₁D₁ có cạnh bằng 1. Gọi M, N, P lần lượt là trung điểm của các cạnh BB₁, CD. A₁D₁. Tính khoảng cách và góc giữa hai đường thẳng MP và C₁N.

Lời giải:

Ta chọn hệ trục tọa độ như sau: B₁ là gốc tọa độ, B₁A₁→ = i→, B₁C₁→ = j→, B₁B→ = k→. Trong hệ trục vừa chọn, ta có B1(0; 0; 0), B(0; 0; 1), A1(1; 0; 0), D1(1; 1; 0), C(0; 1; 1), D(1; 1; 1), C1(0; 1; 0).

Suy ra M(0; 0; 1/2), P(1; 1/2; 0), N(1/2; 1; 1)

Ta có MP→ = (1; 1/2; −1/2); C₁N→ = (1/2; 0; 1)

Gọi (α) là mặt phẳng chứa C₁N và song song với MP. (α) có vecto pháp tuyến là n→ = (1/2; −5/4; −14) hay n'→ = (2; −5; −1)

Phương trình của (α) là 2x – 5(y – 1) – z = 0 hay 2x – 5y – z + 5 = 0

Ta có:

d(MP, C₁N) = d(M,(α)) 

Ta có:

Vậy ∠(MP,C₁N) = 90^o.

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về giải SBT toán hình lớp 12 tập 2 Câu hỏi và bài tập chương 3, file PDF hoàn toàn miễn phí.