Giải SBT Toán 9 trang 113, 114, 115, 116, 117 Tập 1 (Chính xác nhất)

Giải bài tập Sách bài tập Toán 9: Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông, được chúng tôi sưu tầm và đăng tải. Đây là lời giải kèm phương pháp giải hay các bài tập trong chương trình sách bài tập Toán 9. Là tài liệu tham khảo hữu ích dành cho các em học sinh và quý thầy cô giáo tham khảo và đối chiếu đáp án chính xác, chuẩn bị tốt cho việc tiếp thu, giảng dạy bài học mới đạt hiệu quả.

Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông

Bài 52 trang 113 Sách bài tập Toán 9 Tập 1: 

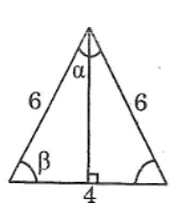
Các cạnh của một tam giác có độ dài 4cm, 6cm và 6cm. Hãy tính góc nhỏ nhất của tam giác đó.

Lời giải:

Vì các cạnh của tam giác lần lượt là 4cm, 6cm và 6cm nên tam giác đó là tam giác cân. Góc nhỏ nhất của tam giác là góc đối diện với cạnh 4cm.

Kẻ đường cao từ đỉnh của góc nhỏ nhất. Đường cao chia cạnh đáy thành hai phần bằng nhau mỗi phần 2cm.

Ta có:

cos β = 2/6 = 1/3 ⇒ β ≈ 70^o32’

Suy ra: α = 180^o – (β+ β) = 180^o – 2.70^o32’ = 38^o56’

Vậy góc nhỏ nhất của tam giác bằng 38^o56’.

Bài 53 trang 113 Sách bài tập Toán 9 Tập 1: 

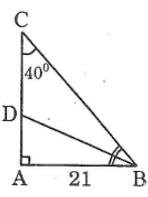
Tam giác ABC vuông tại A có AB = 21cm, góc C = 40^o. Hãy tính các độ dài:

a. AC    

b. BC    

c. Phân giác BD

Lời giải:

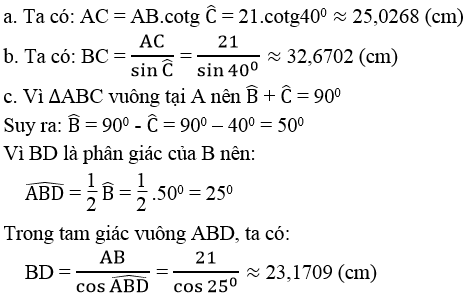
Bài 54 trang 113 Sách bài tập Toán 9 Tập 1: 

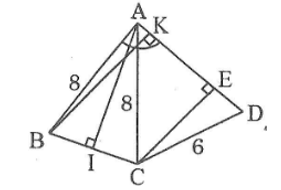
Cho hình bên. Biết AB = AC = 8cm, CD = 6cm,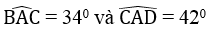 

Hãy tính:

a. Độ dài cạnh BC

b. góc (ADC)

c. Khoảng cách từ điểm B đến cạnh AD

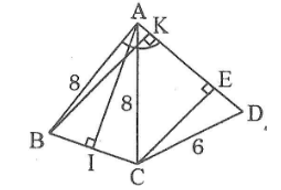
Lời giải:

Bài 55 trang 114 Sách bài tập Toán 9 Tập 1:

Cho tam giác ABC trong đó AB = 5cm, AC = 8cm, góc (BAC) = 20^o

Tính diện tích tam giác ABC, có thể dùng các thông tin dưới đây nếu cần:

sin20^o ≈ 0,3420; cos20^o ≈ 0,9397; tg20^o ≈ 0,3640

Lời giải:

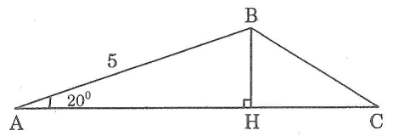
Kẻ BH ⊥ AC.

Trong tam giác vuông ABH, ta có:

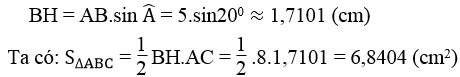
Bài 56 trang 114 Sách bài tập Toán 9 Tập 1: 

Từ đỉnh một ngọn đèn biển cao 38m so với mặt nước biển, người ta nhìn thấy một hòn đảo dưới góc 30^o so với đường nằm ngang chân đèn (hình bên). Hỏi khoảng cách từ đảo đến chân đèn (ở mực nước biển) bằng bao nhiêu?

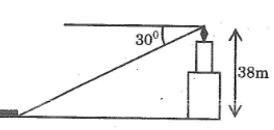
Lời giải:

Khoảng cách từ đảo đến chân cột đèn biển là cạnh kề với góc 30^o, chiều cao của cột đèn biển là cạnh đối diện với góc 30^o

Vậy khoảng cách từ đảo đến chân đèn là:

38.cotg30^o ≈ 65,818 (cm).

Bài 57 trang 114 Sách bài tập Toán 9 Tập 1: 

Trong tam giác ABC có AB = 11cm, 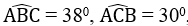 , N là chân đường vuông góc kẻ từ A đến BC. Hãy tính AN, AC

Lời giải:

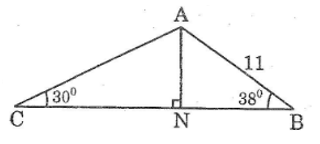
Trong tam giác vuông ABN, ta có:

AN = AB.sin góc B

= 11.sin38^o ≈ 6,772 (cm)

Trong tam giác vuông ACN, ta có:

AC =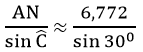 

= 13,544 (cm).

Bài 58 trang 114 Sách bài tập Toán 9 Tập 1: 

Để nhìn thấy đỉnh A của một vách đá dựng đứng, người ta đã đứng tại điểm P cách chân vách đá một khoảng 45m và nhìn lên một góc 250 so với đường nằm ngang (góc nhìn lên này được gọi là góc “nâng”). Hãy tính độ cao của vách đá.

Lời giải:

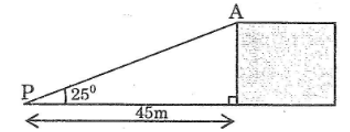
Chiều cao của vách đá là cạnh góc vuông đối diện với góc 25^o

Khi đó chiều cao của vách đá là:

45.tg25^o ≈ 20,984 (m)

Bài 59 trang 114 Sách bài tập Toán 9 Tập 1: 

Tìm x và y trong các hình sau:

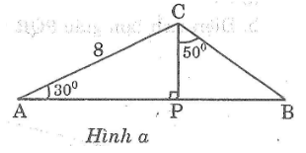
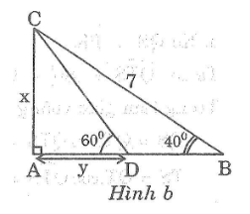
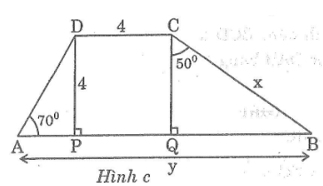
Lời giải:

c. Hình c

Vì tứ giác CDPQ có hai góc vuông và hai cạnh CD = DP = 4 nên nó là hình vuông. Suy ra: CD = DP = PQ = QC = 4

Trong tam giác vuông BCQ, ta có:

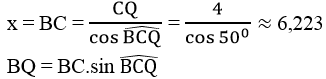
≈ 6,223.sin50^o = 4,767

Trong tam giác vuông ADP, ta có:

AP = DP.cotgA = 4.cotg70^o ≈ 1,456

Ta có: y = AB = AP + PQ + QB = 1,456 + 4 + 4,767 = 10,223.

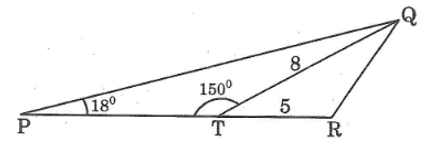
Bài 60 trang 115 Sách bài tập Toán 9 Tập 1: 

Cho hình dưới.

Biết: 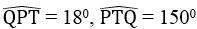 , QT = 8cm, TR = 5cm. Hãy tính:

a. PT

b. Diện tích tam giác PQR

Lời giải:

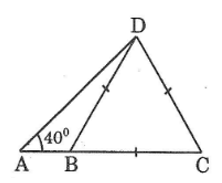
Bài 61 trang 115 Sách bài tập Toán 9 Tập 1: 

Cho hình bên. BCD là tam giác đều cạnh 5cm và góc DAB bằng 40^o. Hãy tính:

a. AD      b. AB

Lời giải:

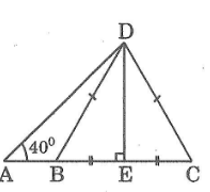
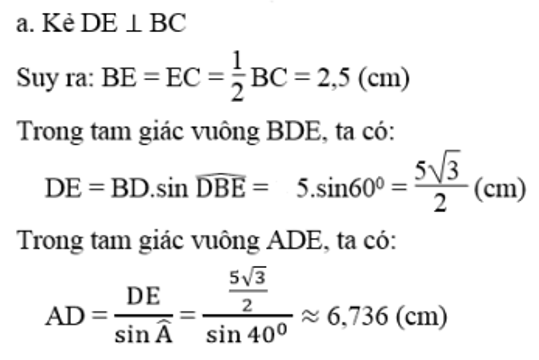
b. Trong tam giác vuông ADE, ta có:

AE = AD.cosA ≈ 6,736.cos40^o

= 5,16 (cm)

Ta có: AB = AE – BE = 5,16 – 2,5 = 2,66 (cm).

Bài 62 trang 115 Sách bài tập Toán 9 Tập 1: 

Cho tam giác ABC vuông tại A, đường cao AH.

Biết HB = 25cm, HC = 64cm. Tính góc B , C

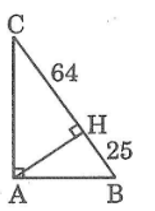
Lời giải:

Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:

AH² = HB.HC

Suy ra:

Bài 63 trang 115 Sách bài tập Toán 9 Tập 1: 

Cho tam giác ABC có BC = 12cm,góc B = 60^o, góc C = 40^o. Tính:

a. Đường cao CH và cạnh AC

b. Diện tích tam giác ABC

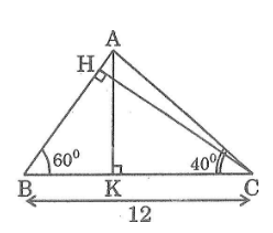
Lời giải:

Bài 64 trang 115 Sách bài tập Toán 9 Tập 1: 

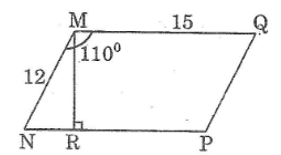
Tính diện tích của hình bình hành có hai cạnh 12cm và 15cm, góc tạo bởi hai cạnh ấy bằng 110^o.

Lời giải:

Giả sử hình bình hành MNPQ có MN = 12cm, MQ = 15cm, góc NMQ = 1100

Ta có: góc NMQ + góc MNP = 180^o (hai góc trong cùng phía)

Suy ra: góc MNP = 180^o - góc NMQ

= 180^o – 110^o = 70^o

Kẻ MR ⊥ NP

Trong tam giác vuông MNR, ta có:

MR = MN.sin góc MNP =12.sin70^o ≈ 11,276 (cm)

Vậy S_MNPQ = MN.NP ≈ 11,276.15 = 169,14 (cm²).

Bài 65 trang 115 Sách bài tập Toán 9 Tập 1: 

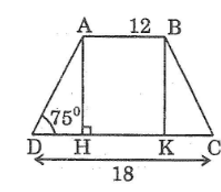
Tính diện tích hình thang cân, biết hai cạnh đáy là 12cm và 18cm, góc ở đáy bằng 75^o

Lời giải:

Giả sử hình thang cân ABCD có AB = 12cm, CD = 18cm,góc D = 75^o

Kẻ AH ⊥ CD, BK ⊥ CD

Vì tứ giác ABKH là hình chữ nhật nên: AB = HK = 12 (cm)

Ta có: ∆ADH = ∆BCK (cạnh huyền, góc nhọn)

Suy ra: DH = CK

Bài 66 trang 115 Sách bài tập Toán 9 Tập 1: 

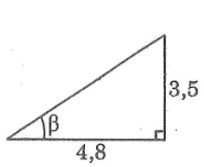
Một cột cờ cao 3,5m có bóng trên mặt đất dài 4,8m. Hỏi góc giữa tia sáng mặt trời và bóng cột cờ là bao nhiêu?

Lời giải:

Chiều cao cột cờ là cạnh đối diện với góc giữa tia sáng mặt trời và bóng cột cờ, chiều dài bóng là cạnh kề góc nhọn.

Ta có: tg β = 3,5/4,8 = 35/48

Suy ra: β = 36^o6’

Bài 67 trang 115 Sách bài tập Toán 9 Tập 1: 

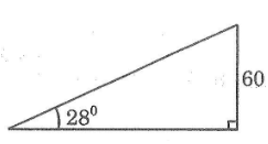
Từ đỉnh một tòa nhà cao 60m, người ta nhìn thấy một chiếc ô tô đang đỗ dưới một góc 28^o so với đường ngang. Hỏi chiếc ô tô đang đỗ cách tòa nhà đó bao nhiêu mét?

Lời giải:

Khoảng cách từ xe ô tô đến tòa nhà là cạnh kề với góc 28^o, chiều cao tòa nhà là cạnh đối với góc nhọn.

Vậy chiếc ô tô đang đỗ cách tòa nhà:

60.cotg28^o ≈ 112,844 (m)

Bài 68 trang 116 Sách bài tập Toán 9 Tập 1: 

Một em học sinh đang đứng ở cách mặt đất tháp ăng-ten 150m. Biết rằng em nhìn thấy đỉnh tháp ở góc 20^o so với đường nằm ngang, khoảng cách từ mắt đến mặt đất bằng 1,5m. Hãy tính chiều cao của tháp.

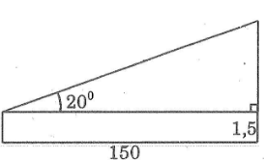
Lời giải:

Phần còn lại của cột ăng-ten là cạnh đối của góc 20^o, khoảng cách từ chỗ em đứng đến chân cột ăng-ten là cạnh kề với góc 20^o.

Phần còn lại của cột ăng-ten cao là:

150.tg20^o ≈ 54,596 (m)

Chiều cao của cột ăng-ten là:

54,596 + 1,5 = 56,096 (m)

Bài 69 trang 116 Sách bài tập Toán 9 Tập 1: 

Hai cột thẳng đứng của hai trại A và B (của lớp 9A và lớp 9B) cách nhau 8m. Từ một cái cọc ở chính giữa hai cột, người ta đo được góc giữa các dây căng từ đỉnh hai cột của hai trại A và B đến cọc tạo với mặt đất lần lượt là 35^o và 30^o. Hỏi trại nào cao hơn và cao hơn bao nhiêu mét?

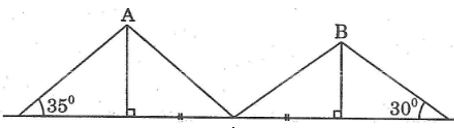
Lời giải:

Chiều cao trại A là cạnh góc vuông đối diện với góc nhọn 35^o, chiều cao trại B là cạnh góc vuông đối diện với góc nhọn 30^o, cạnh kề với hai góc nhọn bằng nhau bằng 4m.

Chiều cao trại A là: 4.tg35^o ≈ 2,801 (m)

Chiều cao trại B là: 4.tg30^o ≈ 2,309 (m)

Trại A cao hơn trại B là: 2,801 – 2,309 = 0,492 (m)

Bài 70 trang 116 Sách bài tập Toán 9 Tập 1: 

Một người trinh sát đứng cách một tòa nhà khoảng 10m. Góc “nâng” từ chỗ anh ta đứng đến nóc tòa nhà là 40^o (hình bên)

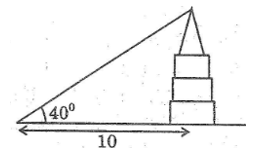
a. Tính chiều cao của tòa nhà

b. Nếu anh ta dịch chuyển sao cho góc “nâng” là 35^o thì anh ta cách tòa nhà bao nhiêu mét? Khi đó anh ta tiến lại gần hay ra xa ngôi nhà?

Lời giải:

a. Chiều cao tòa nhà là cạnh góc vuông đối diện với góc 40^o, khoảng cách từ chỗ người trinh sát đứng đến ngôi nhà là cạnh kề.

Chiều cao của tòa nhà là:

10.tg40^o ≈ 8,391 (m)

b. Nếu dịch chuyển sao cho góc “nâng” là 35^o thì anh ta cách tòa nhà:

8,391.cotg35^o ≈ 11,934 (m)

Bài 71 trang 116 Sách bài tập Toán 9 Tập 1: 

Một chiếc diều ABCD có AB = BC, AD = DC. Biết AB = 12cm, 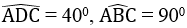 (hình bên). Hãy tính:

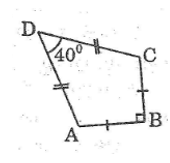
a. Chiều dài cạnh AD.

b. Diện tích của chiếc diều.

Lời giải:

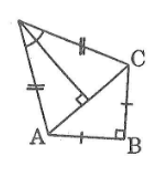
a. Nối AC và kẻ DH ⊥ AC

Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:

AC² = AB²+ BC² = 12² + 12² = 144 + 144 = 288

Suy ra: AC = 12√2 (cm)

Ta có: ∆ACD cân tại D

DH ⊥ AC

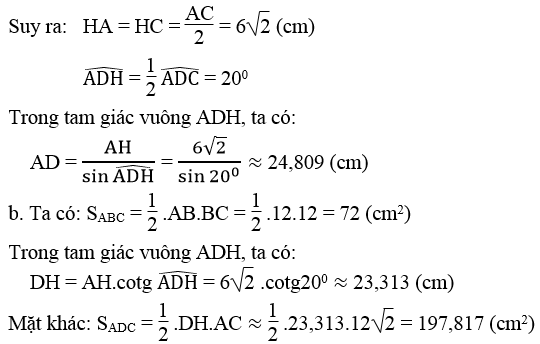
Vậy S_diều = S_ABC + S_ADC = 72 + 197,817 = 269,817 (cm²).

Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích đầy đủ các môn được cập nhật liên tục tại chuyên trang của chúng tôi.

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Lời giải sách bài tập Toán 9 Tập 1 trang 113, 114, 115, 116, 117: Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông.