Giải SBT Toán Hình 9 trang 167, 168 Tập 1 (Chính xác nhất)

Giải bài tập sách bài tập Toán Hình lớp 9: Bài 7: Vị trí tương đối của hai đường tròn được chúng tôi sưu tầm và đăng tải. Đây là lời giải kèm phương pháp giải hay các bài tập trong chương trình Sách bài tập Toán 9. Là tài liệu tham khảo hữu ích dành cho các em học sinh và quý thầy cô giáo tham khảo và đối chiếu đáp án chính xác, chuẩn bị tốt cho việc tiếp thu, giảng dạy bài học mới đạt hiệu quả.

Bài 7: Vị trí tương đối của hai đường tròn

Bài 64 trang 167 Sách bài tập Toán 9 Tập 1: 

Cho hình bên, trong đó hai đường tròn (O) và (O’) tiếp xúc với nhau tại A. Chứng minh rằng các tiếp tuyến Bx và Cy song song với nhau.

Lời giải:

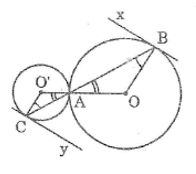
Ta có: O, A, O’ thẳng hàng

C, A, B thẳng hàng

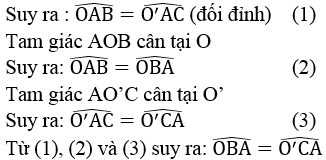
Suy ra OB // O’C (vì có cặp góc so le trong bằng nhau)

Lại có: Bx ⊥ OB (tính chất tiếp tuyến)

Suy ra: Bx ⊥ O’C

Mà: Cy ⊥ O’C (tính chất tiếp tuyến)

Suy ra: Bx // Cy

Bài 65 trang 167 Sách bài tập Toán 9 Tập 1: 

Cho hai đường tròn (O) và (O’) cắt nhau tại A và B như hình bên.

Biết OA = 15cm, O’A = 13cm, AB = 24cm. Tính độ dài OO’.

Lời giải:

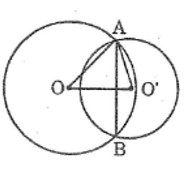
Gọi H là giao điểm của AB và OO’.

Vì OO’ là đường trung trực của AB nên:

OO’ ⊥ AB tại H

Suy ra: HA = HB = (1/2).AB = (1/2).24 = 12 (cm)

Áp dụng định lí Pitago vào tam giác vuông AOH, ta có:

AO² = OH² + AH²

Suy ra: OH² = OA² – AH² = 15² – 12² = 81

OH = 9 (cm)

Áp dụng định lí pitago vào tam giác vuông AO’H, ta có:

AO’² = O’H² + AH²

Suy ra: O’H²= O’A²– AH² = 13² – 12² = 25

O’H = 5 (cm)

Vậy OO’ = OH + O’H = 9 + 5 = 14 (cm)

Bài 67 trang 167 Sách bài tập Toán 9 Tập 1: 

Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Kẻ các đường kính AOC, AO’D. Chứng minh rằng ba điểm C, B, D thẳng hàng và AB ⊥ CD

Lời giải:

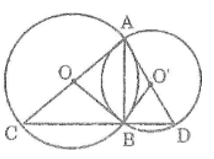
Tam giác ABC nội tiếp trong đường tròn (O) có AC là đường kính nên góc (ABC) = 90^o

Tam giác ABD nội tiếp trong đường tròn (O’) có AD là đường kính nên góc (ABD) = 90^o

Ta có:

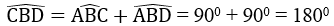
Vậy ba điểm C, B, D thẳng hàng và AB ⊥ CD.

Bài 68 trang 168 Sách bài tập Toán 9 Tập 1: 

Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Gọi I là trung điểm của OO’. Qua A vẽ đường thẳng vuông góc với IA, cắt các đường tròn (O) và (O’) tại C và D (khác A). Chứng minh rằng AC = AD

Lời giải:

Kẻ OH ⊥ CD, O’K ⊥ CD

Ta có: IA ⊥ CD

Suy ra : OH // IA // O’K

Theo giả thiết : IO = IO’

Suy ra : AH = AK (tính chất đường thẳng song song cách đều) (1)

Ta có : OH ⊥ AC

Suy ra : HA = HC = (1/2).AC (đường kính dây cung) ⇒ AC = 2AH (2)

Lại có : O’K ⊥ AD

Suy ra : KA = KD = (1/2).AD (đường kính dây cung) ⇒ AD = 2AK (3)

Từ (1), (2) và (3) suy ra: AC = AD

Bài 69 trang 168 Sách bài tập Toán 9 Tập 1: 

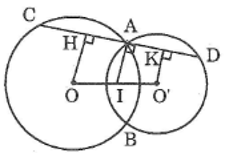
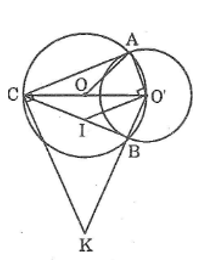
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B, trong đó O’ nằm trên đường tròn (O). Kẻ đường kính O’OC của đường tròn (O).

a. Chứng minh rằng CA, CB là các tiếp tuyến của đường tròn (o’)

b. Đường vuông góc với AO’ tại O’ cắt CB ở I. Đường vuông góc với AC tại C cắt đường thẳng O’B ở K. Chứng minh rằng ba điểm O, I, K thẳng hàng.

Lời giải:

a. Tam giác AO’C nội tiếp trong đường tròn (O) có O’C là đường kính nên góc O'AC = 90^o

Suy ra: CA ⊥ O’A tại điểm A

Vậy CA là tiếp tuyến của đường tròn (O’)

Tam giác BO’C nội tiếp trong đường tròn (O) có O’C là đường kính nên góc O'BC = 90^o

Suy ra: CB ⊥ O’B tại điểm B

Vậy CB là tiếp tuyến của đường tròn (O’)

b. Trong đường tròn (O’) ta có AC và BC là hai tiếp tuyến cắt nhau tại C

Suy ra: góc ACO' = góc BCO' (tính chất hai tiếp tuyến cắt nhau)

Mà O’I ⊥ O’A (gt)

CA ⊥ O’A (chứng minh trên)

Suy ra: O’I // CA => góc ACO' = góc CO'I (hai góc so le trong)

Suy ra: góc BCO' = góc CO'I

Hay tam giác CIO’ cân tại I => IC = IO’

Khi đó I nằm trên đường trung trực của O’C

Lại có: góc AO'C = góc BO'C (tính chất hai tiếp tuyến cắt nhau)

KC ⊥ CA (gt)

O’A ⊥ AC (chứng minh trên)

Suy ra: KC // O’A => góc AO'C = góc O'CK (hai góc so le trong)

Suy ra: góc O'CK = góc KO'C

Hay tam giác CKO’ cân tại K => KC = KO’

Khi đó K nằm trên đường trung trực của O’C

Mặt khác: OC = OO’ (= R)

Suy ra O, I, K nằm trên đường trung trực của O’C

Vậy O, I, K thẳng hàng.

Bài 70 trang 168 Sách bài tập Toán 9 Tập 1: 

Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Dây AC của đường tròn (O) tiếp xúc với đường tròn (O’) tại A. Dây AD của đường trong (O’) tiếp xúc với đường tròn (O) tại A. Gọi K là điểm đối xứng với A qua trung điểm I của OO’, E là điểm đối xứng với A qua B. Chứng minh rằng:

a. AB ⊥ KB

b. Bốn điểm A, C, E, D cùng nằm trên một đường tròn

Lời giải:

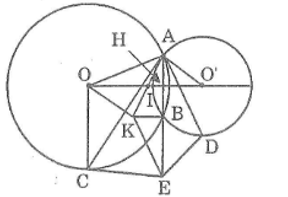
a. Gọi H là giao điểm của AB và OO’

Vì OO’ là đường trung trực của AB nên OO’ ⊥ AB tại H

Ta có: HA = HB

I là trung điểm của OO’ nên IH ⊥ AB     (1)

Trong tam giác ABK, ta có:

HA = HB (chứng minh trên)

IA = IK (tính chất đối xứng tâm)

Suy ra IH là đường trung bình của tam giác ABK

Suy ra IH // BK     (2)

Từ (1) và (2) suy ra: AB ⊥ KB

b. Vì AB ⊥ KB nên AE ⊥ KB

Lại có: AB = BE (tính chất đối xứng tâm)

Suy ra: KA = KE (tính chất đường trung trực)     (3)

Ta có: IO = IO’ (gt)

IA = IK (chứng minh trên)

Tứ giác AOKO’ có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành

Suy ra: OK // O’A và OA // O’K

CA ⊥ O’A (vì CA là tiếp tuyến của đường tròn (O’))

OK // O’A (chứng minh trên)

Suy ra: OK ⊥ AC

Khi đó OK là đường trung trực của AC

Suy ra: KA = KC (tính chất đường trung trực)     (4)

DA ⊥ OA (vì DA là tiếp tuyến của đường tròn (O))

O’K // OA (chứng minh trên)

Suy ra: O’K ⊥ DA

Khi đó O’K là đường trung trực của AD

Suy ra: KA = KD (tính chất đường trung trực)     (5)

Từ (3), (4) và (5) suy ra: KA = KC = KE = KD

Vậy bốn điểm A, C, E, D cùng nằm trên một đường tròn.3

Bài tập bổ sung (trang 168)​​​​​​​

Bài 1 trang 168 Sách bài tập Toán 9 Tập 1: 

Cho h.bs.23, trong đó OA = 3, O’A = 2, AB = 5. Độ dài AC bằng

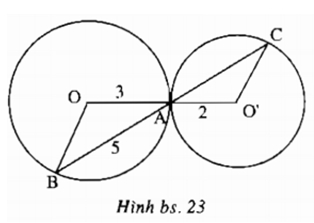
A. 10/3;       

B. 3,5;

C. 3;       

D. 4.

Hãy chọn phương án đúng.

Lời giải:

Chọn đáp án A

Bài 2 trang 168 Sách bài tập Toán 9 Tập 1: 

Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Một đường thẳng vuông góc với AB tại B cắt đường tròn (O) và (O’) theo thứ tự C và D (khác B). Chứng minh rằng OO’ = 1/2CD.

Lời giải:

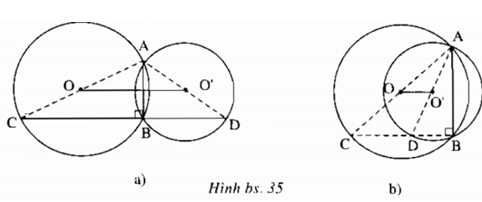
∠(ABC) = 90^o nên A, O, C thẳng hàng.

∠(ABD) = 90^o nên A, O’, D thẳng hàng.

OO’ là đường trung bình của tam giác ΔACD nên OO’ = 1/2CD.

Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích đầy đủ các môn được cập nhật liên tục tại chuyên trang của chúng tôi.

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải SBT Toán Hình 9  trang 167, 168: Bài 7: Vị trí tương đối của hai đường tròn file Word, pdf hoàn toàn miễn phí!