Giải SBT Toán Hình 9 trang 103, 104 Tập 2 (Chính xác nhất)

Giải bài tập sách bài tập Toán Hình lớp 9: Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung được chúng tôi sưu tầm và đăng tải. Đây là lời giải kèm phương pháp giải hay các bài tập trong chương trình Sách bài tập Toán 9. Là tài liệu tham khảo hữu ích dành cho các em học sinh và quý thầy cô giáo tham khảo và đối chiếu đáp án chính xác, chuẩn bị tốt cho việc tiếp thu, giảng dạy bài học mới đạt hiệu quả.

Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung

Bài 24 trang 103 Sách bài tập Toán 9 Tập 2: 

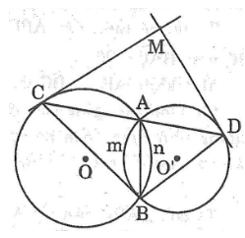
Hai đường tròn (O) và (O’) cắt nhau tại A và B. Qua A vẽ cát tuyến CAD với hai đường tròn (C ∈ (O) ,D ∈ (O’))

a. Chứng minh rằng khi cát tuyến quay xung quanh điểm A thì góc CBD có số đo không đổi

b. Từ C và D vẽ hai tiếp tuyến với đường tròn.Chứng minh rằng hai tiếp tuyến này hợp với nhau một góc có số đo không đổi khi cát tuyến CAD quay xung quanh điểm A

Lời giải:

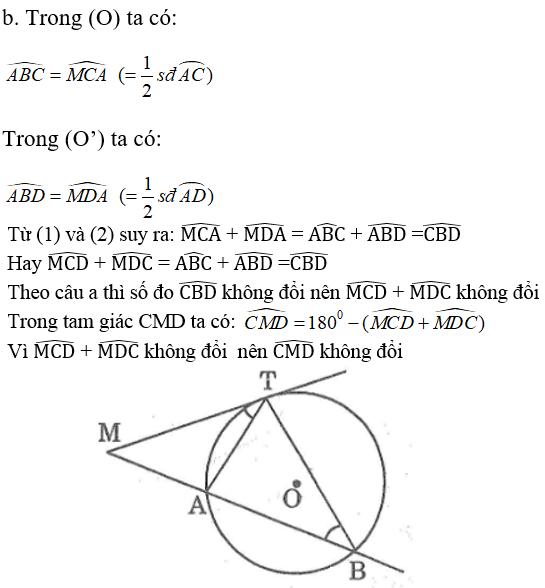
Bài 25 trang 104 Sách bài tập Toán 9 Tập 2: 

Từ một điểm M cố định ở bên ngoài đường tròn (O), kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó

a. Chứng minh rằng luôn có MT²= MA.MB và tích này không phụ thuộc vị trí của cát tuyến MAB

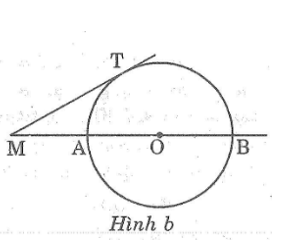
b. Cho MT = 20cm ,MB = 50cm,tính bán kính đường tròn

Lời giải:

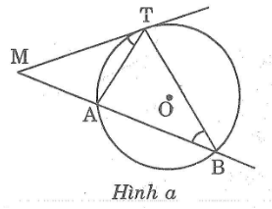
Vì cát tuyến MAB kẻ tùy ý nên ta luôn có MT² = MA.MB không phụ thuộc vị trí của cát tuyến MAB.

b. Gọi bán kính của đường tròn (O) là R

Ta có:MB=MA+AB = MA + 2R

Suy ra: MA =MB – 2R

Ta lại có: MT²= MA.MB (cmt)

Suy ra: MT²= (MB- 2R).MB = MB² – 2R.MB

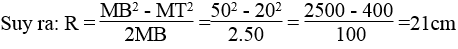
Bài 26 trang 104 Sách bài tập Toán 9 Tập 2: 

Ngồi trên đỉnh núi cao 1 km thì có thể nhìn thấy một địa điểm T trên mặt đất với khoảng cách tối đa là bao nhiêu ? Biết rằng bán kính Trái Đất gần bằng 6400 km

Lời giải:

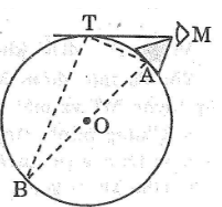
Điểm nhìn tối đa T là tiếp điểm của tiếp tuyến kẻ từ mắt đến bề mặt Trái Đất (như hình vẽ)

Xét hai tam giác MTA và MBT,ta có:

góc M chung

góc MTA = góc MBT

(hệ quả góc giữa tiếp tuyến và dây cung)

Suy ra ΔMTA đồng dạng ΔMBT

⇒ MT/MA = MB/MT => MT²= MA.MB

= MA (MA + 2R)

MA là chiều cao của đỉnh núi bằng 1km

Thay số ta có: MT²=1.(1 + 2.6400)=12801

Suy ra : MT ≈ 113,1(km).

Bài 27 trang 104 Sách bài tập Toán 9 Tập 2: 

Cho tam giác ABC nội tiếp trong đường tròn (O).Vẽ tia Bx sao cho tia BC nằm giữa hai tia Bx,BA và góc CBx = góc BAC .Chứng minh rằng Bx là tiếp tuyến của (O).

Lời giải:

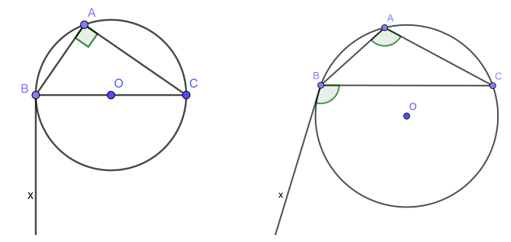
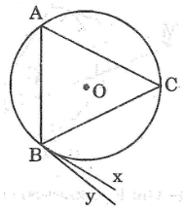
Tam giác ABC nội tiếp đường tròn có 3 trường hợp xảy ra: tam giác nhọn, tam giác vuông, tam giác tù ( hình vẽ)

Xét trường hợp: Tam giác ABC vuông.

Khi đó BC là đường kính của đường tròn O

góc CBx = góc BAC = 90^o

Suy ra, tia Bx vuông góc với bán kính OB

Vậy Bx là tia tiếp tuyến của (O)

Xét trường hợp tam giác ABC nhọn hoặc tù

Giả sử Bx không phải là tiếp tuyến của đường tròn (O).Khi đó,trên cùng nửa mặt phẳng bờ đường thẳng BC chứa tia Bx kẻ tia By là tiếp tuyến của (O) tại B

Ta có:

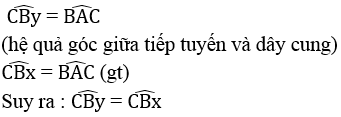
Bx và By là hai tia khác nhau nằm trên cùng một nửa mặt phẳng bờ BC tạo với BC một góc bằng nhau, trái với tính chất đặt tia trên nửa mặt phẳng .Điều này mâu thuẫn với giả sử Bx không phải là tiếp tuyến của đường tròn (O)

Vậy Bx là tiếp tuyến của đường tròn (O).

Bài tập bổ sung (trang 104)

Bài 1 trang 104 Sách bài tập Toán 9 Tập 2: 

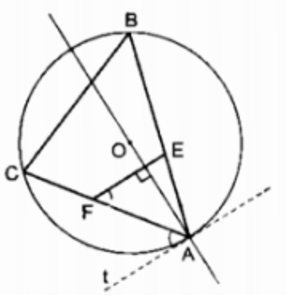
Cho đường tròn tâm O bán kính R. Lấy ba điểm bất kỳ A, B, C trên đường tròn (O). Điểm E bất kỳ thuôc đoạn thẳng AB (và không trùng với A, B). Đường thẳng d đi qua điểm E và vuông góc với đường thẳng OA cắt đoạn thẳng AC tại điểm F.

Chứng minh: góc BCF + góc BEF = 180^o

Lời giải:

Bài 2 trang 104 Sách bài tập Toán 9 Tập 2: 

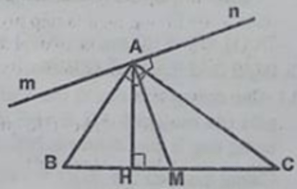
Cho tam giác ABC vuông ở A, AH và AM tương ứng là đường cao và đường trung tuyến kẻ từ A của tam giác đó. Qua điểm A kẻ đường thẳng mn vuông góc với AM. Chứng minh: AB và AC tương ứng là tia phân giác của các góc tạo bở AH và hai tia Am, An của đường thẳng mn.

Lời giải:

Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích đầy đủ các môn được cập nhật liên tục tại chuyên trang của chúng tôi.

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải SBT Toán Hình 9 trang 103, 104: Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung file Word, pdf hoàn toàn miễn phí!