Giải SBT Toán 9 trang 14, 15, 16 Tập 1 (Chính xác nhất)

Giải bài tập Sách bài tập Toán 9 Bài 6: Biến đổi đơn giản biểu thức chứa căn thức bậc hai được chúng tôi sưu tầm và đăng tải. Đây là lời giải kèm phương pháp giải hay các bài tập trong chương trình sách bài tập Toán 9. Là tài liệu tham khảo hữu ích dành cho các em học sinh và quý thầy cô giáo tham khảo và đối chiếu đáp án chính xác, chuẩn bị tốt cho việc tiếp thu, giảng dạy bài học mới đạt hiệu quả.

Giải bài tập SBT Toán lớp 9 Bài 6: Biến đổi đơn giản biểu thức chứa căn thức bậc hai

Bài 56 trang 14 Sách bài tập Toán 9 Tập 1: 

Đưa thừa số ra ngoài dấu căn:

Lời giải:

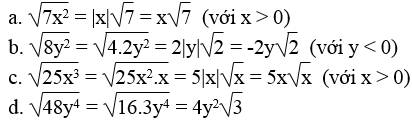
Bài 57 trang 14 Sách bài tập Toán 9 Tập 1: 

Đưa thừa số vào trong dấu căn:

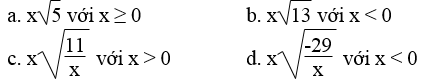
Lời giải:

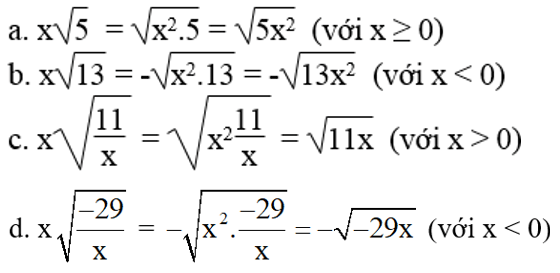
Bài 58 trang 14 Sách bài tập Toán 9 Tập 1: 

Rút gọn các biểu thức:

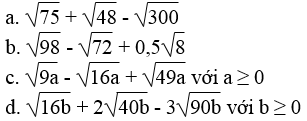
Lời giải:

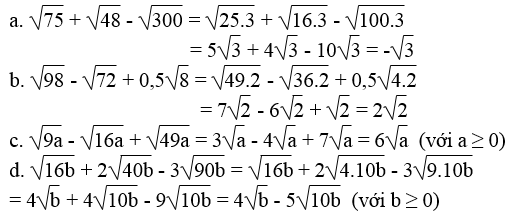
Bài 59 trang 14 Sách bài tập Toán 9 Tập 1: 

Rút gọn biểu thức:

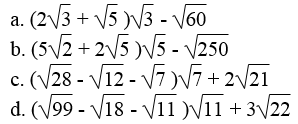
Lời giải:

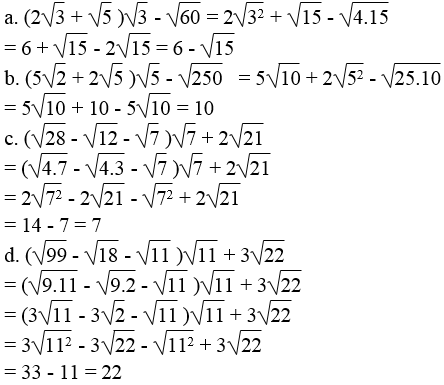
Bài 60 trang 15 Sách bài tập Toán 9 Tập 1: 

Rút gọn các biểu thức:

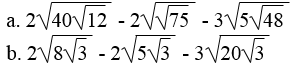
Lời giải:

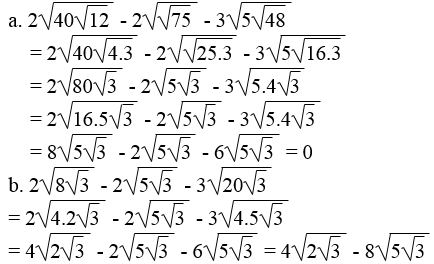
Bài 61 trang 15 Sách bài tập Toán 9 Tập 1: 

Khai triển và rút gọn các biểu thức (với x và y không âm)

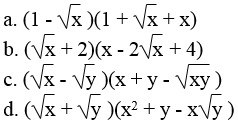
Lời giải:

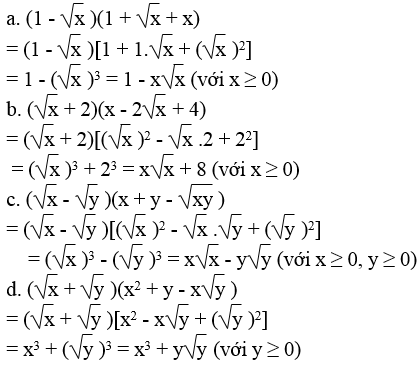
Bài 62 trang 15 Sách bài tập Toán 9 Tập 1: 

Khai triển và rút gọn các biểu thức (với x và y không âm)

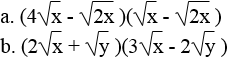
Lời giải:

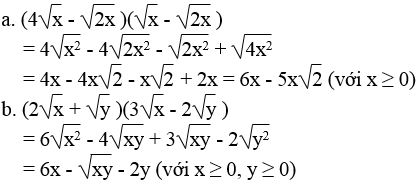
Bài 63 trang 15 Sách bài tập Toán 9 Tập 1: 

Chứng minh:

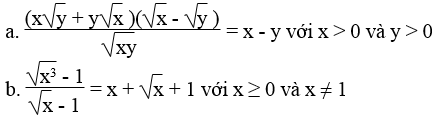
Lời giải:

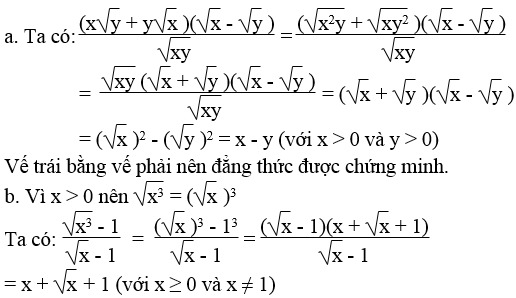
Bài 64 trang 15 Sách bài tập Toán 9 Tập 1: 

a. Chứng minh: 

b. Rút gọn biểu thức: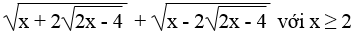 

Lời giải:

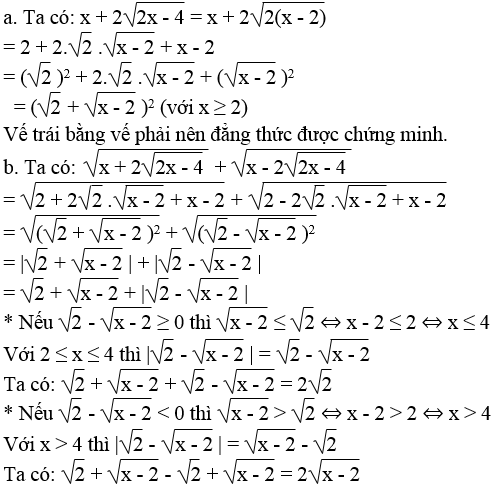
Bài 65 trang 15 Sách bài tập Toán 9 Tập 1: 

Tìm x, biết:

Lời giải:

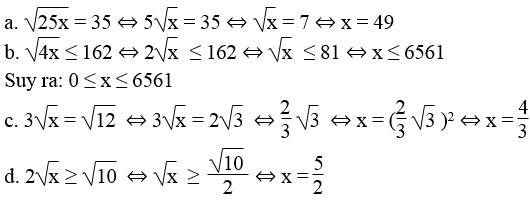
Bài 66 trang 15 Sách bài tập Toán 9 Tập 1: 

Tìm x, biết:

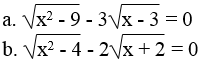
Lời giải:

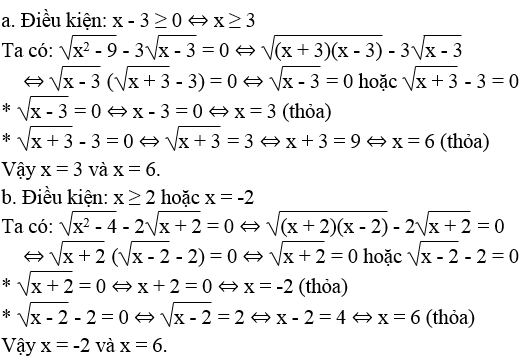
Bài 67 trang 15 Sách bài tập Toán 9 Tập 1: 

Áp dụng bất đẳng thức Cô-si cho hai số không âm, chứng minh:

a. Trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất.

b. Trong các hình chữ nhật có cùng diện tích thì hình vuông có chu vi bé nhất.

Lời giải:

Với hai số không âm a và b, bất đẳng thức Cô-si cho hai số đó là:

(a + b)/2 ≥ √ab

a. Các hình chữ nhật có cùng chu vi thì (a + b)/2 không đổi. Từ bất đẳng thức (a + b)/2 ≥ √ab và (a + b)/2 không đổi suy ra ab đạt giá trị lớn nhất bằng (a + b)/2 khi a = b.

Điều này cho thấy trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất.

b. Các hình chữ nhật có cùng diện tích thì ab không đổi. Từ bất đẳng thức (a + b)/2 ≥ √ab và ab không đổi suy ra (a + b)/2 đạt giá trị nhỏ nhât bằng ab khi a = b.

Điều này cho thấy trong các hình chữ nhật có cùng diện tích thì hình vuông có chu vi bé nhất.

Bài 1 trang 16 Sách bài tập Toán 9 Tập 1 (Bài bổ xung):

Rút gọn biểu thức 3√(x²y) + x√y với x < 0, y ≥ 0 ta được

A. 4x√y;       B. -4x√y;      

C. -2x√y;       D. 4√(x^2 y).

Hãy chọn đáp án đúng.

Lời giải:

Chọn đáp án C

Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích đầy đủ các môn được cập nhật liên tục tại chuyên trang của chúng tôi.

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Lời giải sách bài tập Toán 9 Tập 1 trang 14, 15, 16 Bài 6: Biến đổi đơn giản biểu thức chứa căn thức bậc hai.