Giải SBT Toán 9 trang 18, 19, 20 Tập 1 (Chính xác nhất)
Giải bài tập Sách bài tập Toán 9 Bài 8: Rút gọn biểu thức chứa căn thức bậc hai được chúng tôi sưu tầm và đăng tải. Đây là lời giải kèm phương pháp giải hay các bài tập trong chương trình sách bài tập Toán 9. Là tài liệu tham khảo hữu ích dành cho các em học sinh và quý thầy cô giáo tham khảo và đối chiếu đáp án chính xác, chuẩn bị tốt cho việc tiếp thu, giảng dạy bài học mới đạt hiệu quả.
Giải bài tập SBT Toán lớp 9 Bài 8: Rút gọn biểu thức chứa căn thức bậc hai
Bài 80 trang 18 Sách bài tập Toán 9 Tập 1:
Rút gọn các biểu thức:
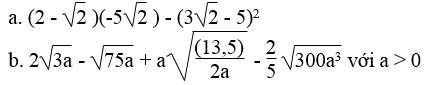
Lời giải:
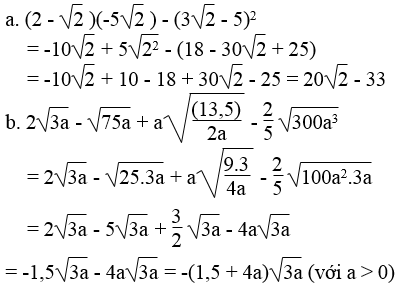
Bài 81 trang 18 Sách bài tập Toán 9 Tập 1:
Rút gọn các biểu thức:
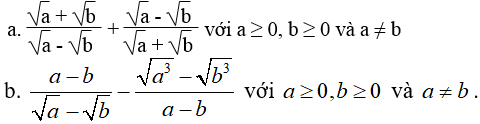
Lời giải:
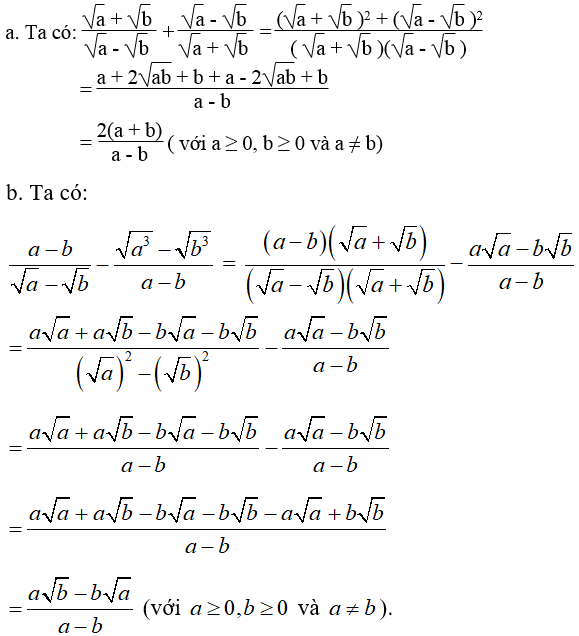
Bài 82 trang 18 Sách bài tập Toán 9 Tập 1:
a. Chứng minh: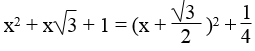 
b. Tìm giá trị nhỏ nhất của biểu thức: x2 + x√3 + 1. Giá trị đó đạt được khi x bằng bao nhiêu?
Lời giải:
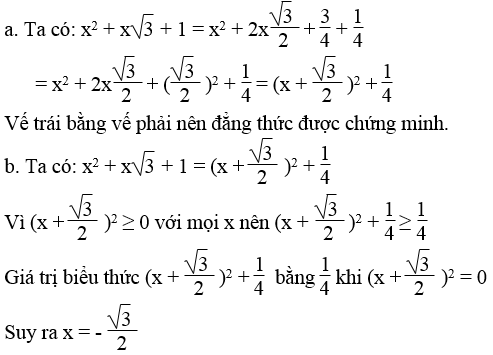
Bài 83 trang 19 Sách bài tập Toán 9 Tập 1:
Chứng tỏ giá trị các biểu thức sau là số hữu tỉ
![](data:image/svg+xml;utf8,<svg style="vertical-align: -2.308ex" xmlns="http://www.w3.org/2000/svg" width="20.75ex" height="5.344ex" role="img" focusable="false" viewBox="0 -1342 9171.3 2362">
<style>
* {
color: black;
background-color: white;
border-radius: 0.25rem;
}
@media (prefers-color-scheme: dark) {
* {
fill: white;
background-color: black;
}
}
</style>
<g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="mi"><path data-c="1D44E" d="M33 157Q33 258 109 349T280 441Q331 441 370 392Q386 422 416 422Q429 422 439 414T449 394Q449 381 412 234T374 68Q374 43 381 35T402 26Q411 27 422 35Q443 55 463 131Q469 151 473 152Q475 153 483 153H487Q506 153 506 144Q506 138 501 117T481 63T449 13Q436 0 417 -8Q409 -10 393 -10Q359 -10 336 5T306 36L300 51Q299 52 296 50Q294 48 292 46Q233 -10 172 -10Q117 -10 75 30T33 157ZM351 328Q351 334 346 350T323 385T277 405Q242 405 210 374T160 293Q131 214 119 129Q119 126 119 118T118 106Q118 61 136 44T179 26Q217 26 254 59T298 110Q300 114 325 217T351 328Z"></path></g><g data-mml-node="mo" transform="translate(529,0)"><path data-c="29" d="M60 749L64 750Q69 750 74 750H86L114 726Q208 641 251 514T294 250Q294 182 284 119T261 12T224 -76T186 -143T145 -194T113 -227T90 -246Q87 -249 86 -250H74Q66 -250 63 -250T58 -247T55 -238Q56 -237 66 -225Q221 -64 221 250T66 725Q56 737 55 738Q55 746 60 749Z"></path></g><g data-mml-node="mfrac" transform="translate(918,0)"><g data-mml-node="mn" transform="translate(1507.7,676)"><path data-c="32" d="M109 429Q82 429 66 447T50 491Q50 562 103 614T235 666Q326 666 387 610T449 465Q449 422 429 383T381 315T301 241Q265 210 201 149L142 93L218 92Q375 92 385 97Q392 99 409 186V189H449V186Q448 183 436 95T421 3V0H50V19V31Q50 38 56 46T86 81Q115 113 136 137Q145 147 170 174T204 211T233 244T261 278T284 308T305 340T320 369T333 401T340 431T343 464Q343 527 309 573T212 619Q179 619 154 602T119 569T109 550Q109 549 114 549Q132 549 151 535T170 489Q170 464 154 447T109 429Z"></path></g><g data-mml-node="mrow" transform="translate(220,-914.5)"><g data-mml-node="msqrt"><g transform="translate(853,0)"><g data-mml-node="mn"><path data-c="37" d="M55 458Q56 460 72 567L88 674Q88 676 108 676H128V672Q128 662 143 655T195 646T364 644H485V605L417 512Q408 500 387 472T360 435T339 403T319 367T305 330T292 284T284 230T278 162T275 80Q275 66 275 52T274 28V19Q270 2 255 -10T221 -22Q210 -22 200 -19T179 0T168 40Q168 198 265 368Q285 400 349 489L395 552H302Q128 552 119 546Q113 543 108 522T98 479L95 458V455H55V458Z"></path></g></g><g data-mml-node="mo" transform="translate(0,94.5)"><path data-c="221A" d="M95 178Q89 178 81 186T72 200T103 230T169 280T207 309Q209 311 212 311H213Q219 311 227 294T281 177Q300 134 312 108L397 -77Q398 -77 501 136T707 565T814 786Q820 800 834 800Q841 800 846 794T853 782V776L620 293L385 -193Q381 -200 366 -200Q357 -200 354 -197Q352 -195 256 15L160 225L144 214Q129 202 113 190T95 178Z"></path></g><rect width="500" height="60" x="853" y="834.5"></rect></g><g data-mml-node="mo" transform="translate(1575.2,0)"><path data-c="2212" d="M84 237T84 250T98 270H679Q694 262 694 250T679 230H98Q84 237 84 250Z"></path></g><g data-mml-node="mn" transform="translate(2575.4,0)"><path data-c="35" d="M164 157Q164 133 148 117T109 101H102Q148 22 224 22Q294 22 326 82Q345 115 345 210Q345 313 318 349Q292 382 260 382H254Q176 382 136 314Q132 307 129 306T114 304Q97 304 95 310Q93 314 93 485V614Q93 664 98 664Q100 666 102 666Q103 666 123 658T178 642T253 634Q324 634 389 662Q397 666 402 666Q410 666 410 648V635Q328 538 205 538Q174 538 149 544L139 546V374Q158 388 169 396T205 412T256 420Q337 420 393 355T449 201Q449 109 385 44T229 -22Q148 -22 99 32T50 154Q50 178 61 192T84 210T107 214Q132 214 148 197T164 157Z"></path></g></g><rect width="3275.4" height="60" x="120" y="220"></rect></g><g data-mml-node="mo" transform="translate(4655.7,0)"><path data-c="2212" d="M84 237T84 250T98 270H679Q694 262 694 250T679 230H98Q84 237 84 250Z"></path></g><g data-mml-node="mfrac" transform="translate(5655.9,0)"><g data-mml-node="mn" transform="translate(1507.7,676)"><path data-c="32" d="M109 429Q82 429 66 447T50 491Q50 562 103 614T235 666Q326 666 387 610T449 465Q449 422 429 383T381 315T301 241Q265 210 201 149L142 93L218 92Q375 92 385 97Q392 99 409 186V189H449V186Q448 183 436 95T421 3V0H50V19V31Q50 38 56 46T86 81Q115 113 136 137Q145 147 170 174T204 211T233 244T261 278T284 308T305 340T320 369T333 401T340 431T343 464Q343 527 309 573T212 619Q179 619 154 602T119 569T109 550Q109 549 114 549Q132 549 151 535T170 489Q170 464 154 447T109 429Z"></path></g><g data-mml-node="mrow" transform="translate(220,-914.5)"><g data-mml-node="msqrt"><g transform="translate(853,0)"><g data-mml-node="mn"><path data-c="37" d="M55 458Q56 460 72 567L88 674Q88 676 108 676H128V672Q128 662 143 655T195 646T364 644H485V605L417 512Q408 500 387 472T360 435T339 403T319 367T305 330T292 284T284 230T278 162T275 80Q275 66 275 52T274 28V19Q270 2 255 -10T221 -22Q210 -22 200 -19T179 0T168 40Q168 198 265 368Q285 400 349 489L395 552H302Q128 552 119 546Q113 543 108 522T98 479L95 458V455H55V458Z"></path></g></g><g data-mml-node="mo" transform="translate(0,94.5)"><path data-c="221A" d="M95 178Q89 178 81 186T72 200T103 230T169 280T207 309Q209 311 212 311H213Q219 311 227 294T281 177Q300 134 312 108L397 -77Q398 -77 501 136T707 565T814 786Q820 800 834 800Q841 800 846 794T853 782V776L620 293L385 -193Q381 -200 366 -200Q357 -200 354 -197Q352 -195 256 15L160 225L144 214Q129 202 113 190T95 178Z"></path></g><rect width="500" height="60" x="853" y="834.5"></rect></g><g data-mml-node="mo" transform="translate(1575.2,0)"><path data-c="2B" d="M56 237T56 250T70 270H369V420L370 570Q380 583 389 583Q402 583 409 568V270H707Q722 262 722 250T707 230H409V-68Q401 -82 391 -82H389H387Q375 -82 369 -68V230H70Q56 237 56 250Z"></path></g><g data-mml-node="mn" transform="translate(2575.4,0)"><path data-c="35" d="M164 157Q164 133 148 117T109 101H102Q148 22 224 22Q294 22 326 82Q345 115 345 210Q345 313 318 349Q292 382 260 382H254Q176 382 136 314Q132 307 129 306T114 304Q97 304 95 310Q93 314 93 485V614Q93 664 98 664Q100 666 102 666Q103 666 123 658T178 642T253 634Q324 634 389 662Q397 666 402 666Q410 666 410 648V635Q328 538 205 538Q174 538 149 544L139 546V374Q158 388 169 396T205 412T256 420Q337 420 393 355T449 201Q449 109 385 44T229 -22Q148 -22 99 32T50 154Q50 178 61 192T84 210T107 214Q132 214 148 197T164 157Z"></path></g></g><rect width="3275.4" height="60" x="120" y="220"></rect></g></g></g></svg>)
![](data:image/svg+xml;utf8,<svg style="vertical-align: -2.308ex" xmlns="http://www.w3.org/2000/svg" width="20.523ex" height="5.997ex" role="img" focusable="false" viewBox="0 -1630.5 9071.3 2650.5">
<style>
* {
color: black;
background-color: white;
border-radius: 0.25rem;
}
@media (prefers-color-scheme: dark) {
* {
fill: white;
background-color: black;
}
}
</style>
<g stroke="currentColor" fill="currentColor" stroke-width="0" transform="scale(1,-1)"><g data-mml-node="math"><g data-mml-node="mi"><path data-c="1D44F" d="M73 647Q73 657 77 670T89 683Q90 683 161 688T234 694Q246 694 246 685T212 542Q204 508 195 472T180 418L176 399Q176 396 182 402Q231 442 283 442Q345 442 383 396T422 280Q422 169 343 79T173 -11Q123 -11 82 27T40 150V159Q40 180 48 217T97 414Q147 611 147 623T109 637Q104 637 101 637H96Q86 637 83 637T76 640T73 647ZM336 325V331Q336 405 275 405Q258 405 240 397T207 376T181 352T163 330L157 322L136 236Q114 150 114 114Q114 66 138 42Q154 26 178 26Q211 26 245 58Q270 81 285 114T318 219Q336 291 336 325Z"></path></g><g data-mml-node="mo" transform="translate(429,0)"><path data-c="29" d="M60 749L64 750Q69 750 74 750H86L114 726Q208 641 251 514T294 250Q294 182 284 119T261 12T224 -76T186 -143T145 -194T113 -227T90 -246Q87 -249 86 -250H74Q66 -250 63 -250T58 -247T55 -238Q56 -237 66 -225Q221 -64 221 250T66 725Q56 737 55 738Q55 746 60 749Z"></path></g><g data-mml-node="mfrac" transform="translate(818,0)"><g data-mml-node="mrow" transform="translate(220,676)"><g data-mml-node="msqrt"><g transform="translate(853,0)"><g data-mml-node="mn"><path data-c="37" d="M55 458Q56 460 72 567L88 674Q88 676 108 676H128V672Q128 662 143 655T195 646T364 644H485V605L417 512Q408 500 387 472T360 435T339 403T319 367T305 330T292 284T284 230T278 162T275 80Q275 66 275 52T274 28V19Q270 2 255 -10T221 -22Q210 -22 200 -19T179 0T168 40Q168 198 265 368Q285 400 349 489L395 552H302Q128 552 119 546Q113 543 108 522T98 479L95 458V455H55V458Z"></path></g></g><g data-mml-node="mo" transform="translate(0,94.5)"><path data-c="221A" d="M95 178Q89 178 81 186T72 200T103 230T169 280T207 309Q209 311 212 311H213Q219 311 227 294T281 177Q300 134 312 108L397 -77Q398 -77 501 136T707 565T814 786Q820 800 834 800Q841 800 846 794T853 782V776L620 293L385 -193Q381 -200 366 -200Q357 -200 354 -197Q352 -195 256 15L160 225L144 214Q129 202 113 190T95 178Z"></path></g><rect width="500" height="60" x="853" y="834.5"></rect></g><g data-mml-node="mo" transform="translate(1575.2,0)"><path data-c="2B" d="M56 237T56 250T70 270H369V420L370 570Q380 583 389 583Q402 583 409 568V270H707Q722 262 722 250T707 230H409V-68Q401 -82 391 -82H389H387Q375 -82 369 -68V230H70Q56 237 56 250Z"></path></g><g data-mml-node="mn" transform="translate(2575.4,0)"><path data-c="35" d="M164 157Q164 133 148 117T109 101H102Q148 22 224 22Q294 22 326 82Q345 115 345 210Q345 313 318 349Q292 382 260 382H254Q176 382 136 314Q132 307 129 306T114 304Q97 304 95 310Q93 314 93 485V614Q93 664 98 664Q100 666 102 666Q103 666 123 658T178 642T253 634Q324 634 389 662Q397 666 402 666Q410 666 410 648V635Q328 538 205 538Q174 538 149 544L139 546V374Q158 388 169 396T205 412T256 420Q337 420 393 355T449 201Q449 109 385 44T229 -22Q148 -22 99 32T50 154Q50 178 61 192T84 210T107 214Q132 214 148 197T164 157Z"></path></g></g><g data-mml-node="mrow" transform="translate(220,-914.5)"><g data-mml-node="msqrt"><g transform="translate(853,0)"><g data-mml-node="mn"><path data-c="37" d="M55 458Q56 460 72 567L88 674Q88 676 108 676H128V672Q128 662 143 655T195 646T364 644H485V605L417 512Q408 500 387 472T360 435T339 403T319 367T305 330T292 284T284 230T278 162T275 80Q275 66 275 52T274 28V19Q270 2 255 -10T221 -22Q210 -22 200 -19T179 0T168 40Q168 198 265 368Q285 400 349 489L395 552H302Q128 552 119 546Q113 543 108 522T98 479L95 458V455H55V458Z"></path></g></g><g data-mml-node="mo" transform="translate(0,94.5)"><path data-c="221A" d="M95 178Q89 178 81 186T72 200T103 230T169 280T207 309Q209 311 212 311H213Q219 311 227 294T281 177Q300 134 312 108L397 -77Q398 -77 501 136T707 565T814 786Q820 800 834 800Q841 800 846 794T853 782V776L620 293L385 -193Q381 -200 366 -200Q357 -200 354 -197Q352 -195 256 15L160 225L144 214Q129 202 113 190T95 178Z"></path></g><rect width="500" height="60" x="853" y="834.5"></rect></g><g data-mml-node="mo" transform="translate(1575.2,0)"><path data-c="2212" d="M84 237T84 250T98 270H679Q694 262 694 250T679 230H98Q84 237 84 250Z"></path></g><g data-mml-node="mn" transform="translate(2575.4,0)"><path data-c="35" d="M164 157Q164 133 148 117T109 101H102Q148 22 224 22Q294 22 326 82Q345 115 345 210Q345 313 318 349Q292 382 260 382H254Q176 382 136 314Q132 307 129 306T114 304Q97 304 95 310Q93 314 93 485V614Q93 664 98 664Q100 666 102 666Q103 666 123 658T178 642T253 634Q324 634 389 662Q397 666 402 666Q410 666 410 648V635Q328 538 205 538Q174 538 149 544L139 546V374Q158 388 169 396T205 412T256 420Q337 420 393 355T449 201Q449 109 385 44T229 -22Q148 -22 99 32T50 154Q50 178 61 192T84 210T107 214Q132 214 148 197T164 157Z"></path></g></g><rect width="3275.4" height="60" x="120" y="220"></rect></g><g data-mml-node="mo" transform="translate(4555.7,0)"><path data-c="2B" d="M56 237T56 250T70 270H369V420L370 570Q380 583 389 583Q402 583 409 568V270H707Q722 262 722 250T707 230H409V-68Q401 -82 391 -82H389H387Q375 -82 369 -68V230H70Q56 237 56 250Z"></path></g><g data-mml-node="mfrac" transform="translate(5555.9,0)"><g data-mml-node="mrow" transform="translate(220,676)"><g data-mml-node="msqrt"><g transform="translate(853,0)"><g data-mml-node="mn"><path data-c="37" d="M55 458Q56 460 72 567L88 674Q88 676 108 676H128V672Q128 662 143 655T195 646T364 644H485V605L417 512Q408 500 387 472T360 435T339 403T319 367T305 330T292 284T284 230T278 162T275 80Q275 66 275 52T274 28V19Q270 2 255 -10T221 -22Q210 -22 200 -19T179 0T168 40Q168 198 265 368Q285 400 349 489L395 552H302Q128 552 119 546Q113 543 108 522T98 479L95 458V455H55V458Z"></path></g></g><g data-mml-node="mo" transform="translate(0,94.5)"><path data-c="221A" d="M95 178Q89 178 81 186T72 200T103 230T169 280T207 309Q209 311 212 311H213Q219 311 227 294T281 177Q300 134 312 108L397 -77Q398 -77 501 136T707 565T814 786Q820 800 834 800Q841 800 846 794T853 782V776L620 293L385 -193Q381 -200 366 -200Q357 -200 354 -197Q352 -195 256 15L160 225L144 214Q129 202 113 190T95 178Z"></path></g><rect width="500" height="60" x="853" y="834.5"></rect></g><g data-mml-node="mo" transform="translate(1575.2,0)"><path data-c="2212" d="M84 237T84 250T98 270H679Q694 262 694 250T679 230H98Q84 237 84 250Z"></path></g><g data-mml-node="mn" transform="translate(2575.4,0)"><path data-c="35" d="M164 157Q164 133 148 117T109 101H102Q148 22 224 22Q294 22 326 82Q345 115 345 210Q345 313 318 349Q292 382 260 382H254Q176 382 136 314Q132 307 129 306T114 304Q97 304 95 310Q93 314 93 485V614Q93 664 98 664Q100 666 102 666Q103 666 123 658T178 642T253 634Q324 634 389 662Q397 666 402 666Q410 666 410 648V635Q328 538 205 538Q174 538 149 544L139 546V374Q158 388 169 396T205 412T256 420Q337 420 393 355T449 201Q449 109 385 44T229 -22Q148 -22 99 32T50 154Q50 178 61 192T84 210T107 214Q132 214 148 197T164 157Z"></path></g></g><g data-mml-node="mrow" transform="translate(220,-914.5)"><g data-mml-node="msqrt"><g transform="translate(853,0)"><g data-mml-node="mn"><path data-c="37" d="M55 458Q56 460 72 567L88 674Q88 676 108 676H128V672Q128 662 143 655T195 646T364 644H485V605L417 512Q408 500 387 472T360 435T339 403T319 367T305 330T292 284T284 230T278 162T275 80Q275 66 275 52T274 28V19Q270 2 255 -10T221 -22Q210 -22 200 -19T179 0T168 40Q168 198 265 368Q285 400 349 489L395 552H302Q128 552 119 546Q113 543 108 522T98 479L95 458V455H55V458Z"></path></g></g><g data-mml-node="mo" transform="translate(0,94.5)"><path data-c="221A" d="M95 178Q89 178 81 186T72 200T103 230T169 280T207 309Q209 311 212 311H213Q219 311 227 294T281 177Q300 134 312 108L397 -77Q398 -77 501 136T707 565T814 786Q820 800 834 800Q841 800 846 794T853 782V776L620 293L385 -193Q381 -200 366 -200Q357 -200 354 -197Q352 -195 256 15L160 225L144 214Q129 202 113 190T95 178Z"></path></g><rect width="500" height="60" x="853" y="834.5"></rect></g><g data-mml-node="mo" transform="translate(1575.2,0)"><path data-c="2B" d="M56 237T56 250T70 270H369V420L370 570Q380 583 389 583Q402 583 409 568V270H707Q722 262 722 250T707 230H409V-68Q401 -82 391 -82H389H387Q375 -82 369 -68V230H70Q56 237 56 250Z"></path></g><g data-mml-node="mn" transform="translate(2575.4,0)"><path data-c="35" d="M164 157Q164 133 148 117T109 101H102Q148 22 224 22Q294 22 326 82Q345 115 345 210Q345 313 318 349Q292 382 260 382H254Q176 382 136 314Q132 307 129 306T114 304Q97 304 95 310Q93 314 93 485V614Q93 664 98 664Q100 666 102 666Q103 666 123 658T178 642T253 634Q324 634 389 662Q397 666 402 666Q410 666 410 648V635Q328 538 205 538Q174 538 149 544L139 546V374Q158 388 169 396T205 412T256 420Q337 420 393 355T449 201Q449 109 385 44T229 -22Q148 -22 99 32T50 154Q50 178 61 192T84 210T107 214Q132 214 148 197T164 157Z"></path></g></g><rect width="3275.4" height="60" x="120" y="220"></rect></g></g></g></svg>)
Lời giải:
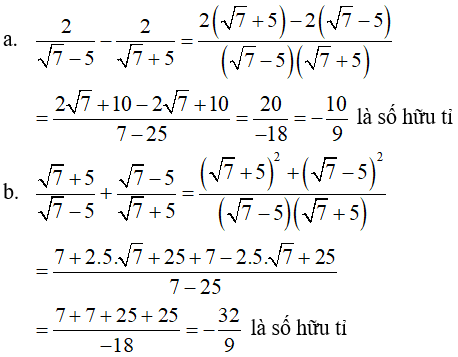
Bài 84 trang 19 Sách bài tập Toán 9 Tập 1:
Tìm x, biết:
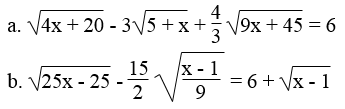
Lời giải:
Bài 85 trang 19 Sách bài tập Toán 9 Tập 1:
Cho biểu thức: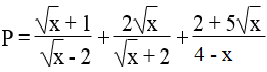 
a. Rút gọn P với x ≥ 0 và x ≠ 4
b. Tìm x để P = 2
Lời giải:
a) Điều kiện: x ≥ 0 và x ≠ 4
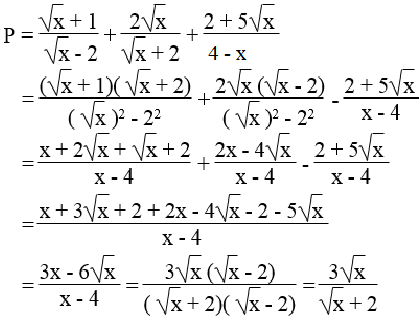
b) Ta có:
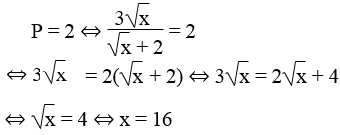
Bài 86 trang 19 Sách bài tập Toán 9 Tập 1:
Cho biểu thức: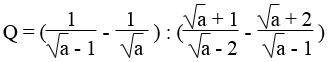 
a. Rút gọn Q với a > 0, a ≠ 4 và a ≠ 1
b. Tìm giá trị của a để Q dương.
Lời giải:
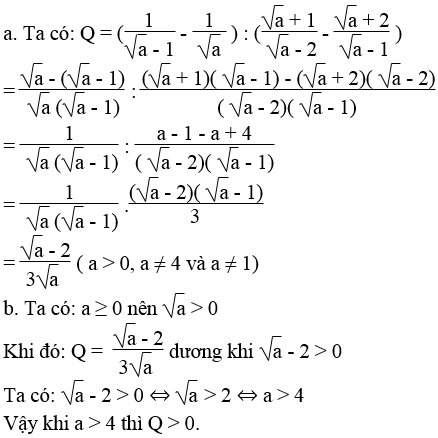
Bài 87 trang 19 Sách bài tập Toán 9 Tập 1:
Với ba số a, b, c không âm, chứng minh bất đẳng thức:
a + b + c ≥ √ab + √bc + √ca
Hãy mở rộng kết quả cho trường hợp bốn số, năm số không âm.
Lời giải:
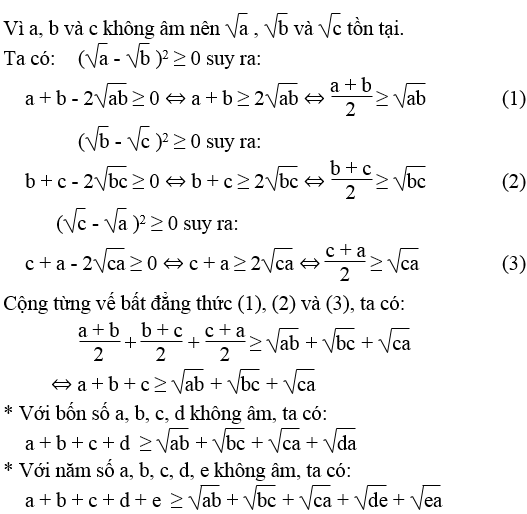
Bài 1 trang 20 Sách bài tập Toán 9 Tập 1 (Bài bổ xung):
Bất phương trình: √32x – (√8 + √2)x > √2 tương đương với bất phương trình
A. √20x > √2; B. 2√5 > √2;
C. 15√2x > √2; D. √2x > √2.
Hãy chọn đáp án đúng.
Lời giải:
Chọn đáp án D
Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích đầy đủ các môn được cập nhật liên tục tại chuyên trang của chúng tôi.
►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Lời giải sách bài tập Toán 9 Tập 1 trang 18, 19, 20 Bài 8: Rút gọn biểu thức chứa căn thức bậc hai.
- Giải SBT Toán 9 trang 64, 65 Tập 1: Bài 3: Đồ thị của hàm số y = ax + b
- Giải SBT Toán 9 trang 14, 15, 16 Tập 1 (Chính xác nhất)
- Giải VBT Toán lớp 9 trang 5, 6, 7 Tập 1: Bài 1: Căn bậc hai
- Giải SBT Toán 9 trang 21, 22, 23 Tập 1: Ôn tập chương 1
- Giải VBT Toán lớp 9 trang 13, 14 Tập 1: Bài 5: Bảng căn bậc hai
- Giải VBT Toán lớp 9 trang 9, 10 Tập 1 (Chính xác nhất)
- Giải VBT Toán lớp 9 trang 10, 11, 12 Tập 1 (Chính xác nhất)
- Giải SBT Toán 9 trang 65, 66, 67 Tập 1 (Đầy đủ)
