Giải SBT Toán Hình 9 trang 105, 106 Tập 2 (Chính xác nhất)

Giải bài tập sách bài tập Toán Hình lớp 9: Bài 6: Cung chứa góc, được chúng tôi sưu tầm và đăng tải. Đây là lời giải kèm phương pháp giải hay các bài tập trong chương trình Sách bài tập Toán 9. Là tài liệu tham khảo hữu ích dành cho các em học sinh và quý thầy cô giáo tham khảo và đối chiếu đáp án chính xác, chuẩn bị tốt cho việc tiếp thu, giảng dạy bài học mới đạt hiệu quả.

Bài 6: Cung chứa góc

Bài 33 trang 105 Sách bài tập Toán 9 Tập 2: 

Cho tam giác ABC có cạnh BC cố định và góc A = α không đổi.Tìm quỹ tích giao điểm của ba đường phân giác trong cuả tam giác

Lời giải:

*Chứng minh thuận:

Gọi I là giao điểm của ba đường phân giác trong của tam giác ABC

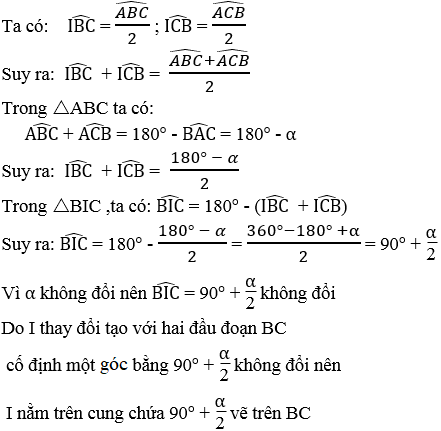
Bài 34 trang 105 Sách bài tập Toán 9 Tập 2: 

Dựng cung chứa góc 42° trên đoạn thẳng AB = 3cm

Lời giải:

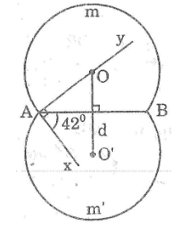
- Dựng đoạn thẳng AB = 3cm

- Vẽ tia Ax sao cho góc (BAx) = 42°

- Dựng đường thẳng d là trung trực của đoạn AB

- Dựng tia Ay sao cho Ay ⊥ Ax (tia Ay cắt đường trung trực d của AB tại O)

- Dựng cung tròn AmB tâm O bán kính OA

- Dựng điểm O’ đối xứng với O qua AB

- Dựng cung tròn (Am'B) tâm O’ bán kính O’A

Ta được hai cung chứa góc 42° trên đoạn thẳng AB = 3cm đối xứng nhau qua AB.

Bài 35 trang 106 Sách bài tập Toán 9 Tập 2: 

Dựng tam giác ABC biết BC = 3cm,góc A = 45° và trung tuyến AM = 2,5cm

Lời giải:

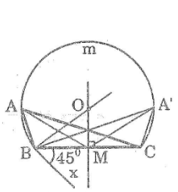
- Dựng đoạn thẳng AB = 3cm

- vẽ tia Bx sao cho góc (CBx) = 45°

- Dựng trung điểm M của BC

- Dựng đường trung trực của BC (qua M)

- Dựng tia vuông góc với Bx tại B ,cắt đường trung trực của BC tại O

- Dựng cung tròn BmC bán kính OB là cung chứa góc 45° vẽ trên đoạn BC

- Dựng đường tròn tâm M bán kính 2,5cm cắt cung BmC lần lượt tại A và A’

- Nối AB , AC (hoặc A’B , A’C) ta có: ΔABC (ΔA’BC) có BC = 3cm , góc A = 45°(hoặc góc (A' ) =45°) và trung tuyến AM =2,5cm.

Bài 36 trang 106 Sách bài tập Toán 9 Tập 2: 

Cho nửa đường tròn đường kính AB cố định. C là một điểm trên nửa đường tròn trên dây AC kéo dài lấy điểm D sao cho CD=CB

a. Tìm quỹ tích các điểm D khi C chạy trên nửa đường tròn đã cho

b. Trên tia CA lấy điểm E sao cho CE = CB.Tìm quỹ tích các điểm E khi C chạy trên nửa đường tròn đã cho

Lời giải:

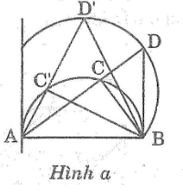
Khi C chuyển động trên nửa đường tròn đường kính AB cố định thì C chuyển động trên cung chứa góc 45° dựng trên đoạn thẳng AB.Khi đó dây AC thay đổi phụ thuộc vào vị trí điểm C trên nửa đường tròn đường kính AB

- dây AC lớn nhất bằng đường kính của đường tròn .Khi C trùng với B thì D cũng trùng với B.vậy B là điểm của quỹ tích

- Dây AC nhỏ nhất có độ dài bằng 0 khi C trùng với A.Khi đó D trùng với B’ là giao điểm của tiếp tuyến đường tròn đường kính AB tại A với cung chứa góc 45° vẽ trên AB

*Chứng minh đảo:

Lấy điểm D’ bất kì trên cung BB' ,nối AD’ cắt đường tròn đường kính AB tại C’.Nối BC’ ,B’D’

Quỹ tích điểm các điểm D khi C chuyển động trên nửa đường tròn đường kính AB là cung BB’ nằm trên cung chứa góc 45° vẽ trên đoạn AB, trong nửa mặt phẳng bờ AB có chứa điểm C (bị giới hạn bởi tiếp tuyến Ax).

b)

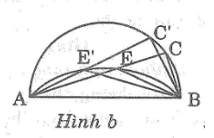
b. Hình b:

*chứng minh thuận

Trong đường tròn đường kính AB ta có:

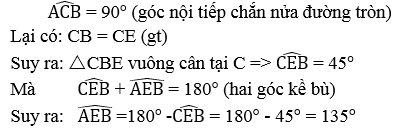
Khi C chuyển động trên đường tròn đường kính AB cố định thì D chuyển động trên cung chứa góc 135° dựng trên đoạn thẳng AB cố định

-Khi dây AC có độ dài lớn nhất bằng đường kính đường tròn thì C trùng với B nên E cũng trùng với B.Vậy B là điểm thuộc quỹ tích

- Khi dây AC có độ dài nhỏ nhất bằng 0 thì C trùng với A.khi đó E trùng với A nên A là một điểm của quỹ tích

Vậy E chuyển động trên cung chứa góc 135° vẽ trên đoạn AB nằm trên nửa mặt phẳng bờ AB chứa điểm C

*chứng minh đảo:

Lấy điểm E’ bất kì trên cung chứa góc 135° , nối AE’ cắt đường tròn đường kính AB tại C’.Nối BE’, BC’

Quỹ tích điểm các điểm E khi C chuyển động trên nửa đường tròn đường kính AB là cung chứa góc 135° vẽ trên đoạn AB, trong nửa mặt phẳng bờ AB có chứa điểm C.

Bài 37 trang 106 Sách bài tập Toán 9 Tập 2: 

Cho nửa đường tròn đường kính AB và C là một điểm trên nửa đường tròn .Trên bán kính OC lấy điểm D sao cho OD bằng khoảng cách CH từ C đến AB. Tìm quỹ tích các điểm D khi C chạy trên nửa đường tròn đã cho

Lời giải:

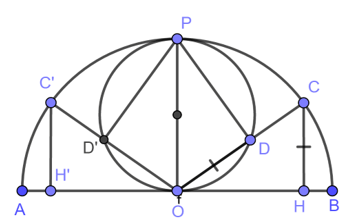
*Chứng minh thuận:

Từ O kẻ đường thẳng vuông góc với AB cắt nửa đường tròn đường kính AB tại P.

Vì O cố dịnh, đường tròn đường kính AB cố định nên P cố định.Nối PD

Ta có: OP // CH (cùng ⊥ AB)

Xét hai tam giác HCO và DOP ta có:

OD = CH (gt)

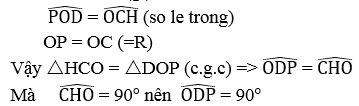
Khi C chuyển động trên nửa đường tròn đường kính AB thì D thay đổi tạo với hai đầu đọan thẳng OP cố định một góc ODP = 90^o

Vậy D chuyển động trên đường tròn đường kính OP

*Chứng minh đảo

Lấy điểm D’ bất kì trên đường tròn đường kính OP ,nối OD’ cắt nửa đường tròn đường kính AB tại C’.Nối PD’ và C’H’ ⊥ AB

Xét hai tam giác C’H’O và PD’O ta có:

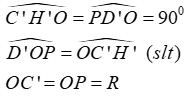
Vậy ΔC’H’O = ΔPD’O (c.g.c) ⇒ C’H’ = OD’

Quỹ tích điểm các điểm D khi C chuyển động trên nửa đường tròn đường kính AB là đường tròn đường kính OP, với OP = AB/2

Bài 38 trang 106 Sách bài tập Toán 9 Tập 2: 

Dựng hình vuông ABCD ,biết đỉnh A , điểm M thuộc cạnh BC và điểm N thuộc cạnh CD

Lời giải:

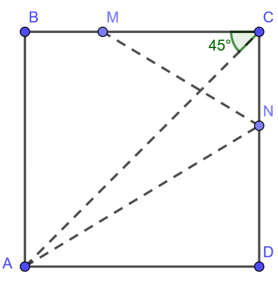
Phân tích: Vì ABCD là hình vuông nên:

Ta có, ba điểm A, M, N cố định nên bài toán quy về việc dựng đỉnh C. Đỉnh C là giao điểm của :

- Cung chứa góc 90° dựng trên đoạn thẳng MN

- Cung chứa góc 45° dựng trên đoạn thẳng AM

Cách dựng:

- Dựng cung chứa góc 90° trên đoạn MN

- Dựng cung chứa góc 45° trên đoạn AM

Hai cung cắt nhau tại C

- Nối CM ,CN

- kẻ AB ⊥ CM tại B , AD ⊥ CN tại D

Tứ giác ABCD là hình vuông cần dựng.

Bài tập bổ sung (trang 106)

Bài 1 trang 106 Sách bài tập Toán 9 Tập 2: 

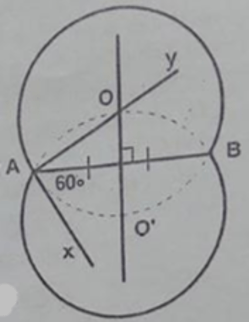
Dựng một cung chứa góc 60⁰ trên đoạn thẳng AB cho trước.

Lời giải:

Cách dựng: − Dựng đoạn thẳng AB.

− Dựng tia Ax sao cho góc BAx = 60^o.

− Dựng đường thẳng d là trung trực của AB.

− Dựng tia Ay ⊥ Ax tại A.

− Tia Ay cắt đường thẳng d tại O.

− Dựng cung tròn tâm O bán kính OA.

− Dựng O' đối xứng với O qua AB.

− Dựng cung tròn tâm O’ bán kính O’A.

Ta có cung chứa góc 60° vẽ trên đoạn AB cho trước.

Bài 2 trang 106 Sách bài tập Toán 9 Tập 2: 

Cho đường tròn tâm O bán kính R và điểm A (khác O) ở trong đường tròn đó.

Một đường thẳng d thay đổi, luôn đi qua A, cắt đường tròn đã cho tại hai điểm là B và C. Tìm quỹ tích trung điểm I của đoạn thẳng BC.

Lời giải:

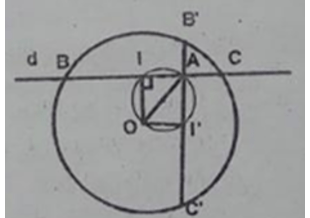
Chứng minh thuận:

Đường tròn (O) cho trước, điểm A cố định nên OA có độ dài không đổi.

ΔOBC cân tại O (vì OB = OC bán kính)

IB = IC (gt) nên OI là đường trung tuyến vừa là đường cao

OI ⊥ BC

Góc OIA = 90^o

Đường thẳng d thay đổi nên B, C thay đổi thì I thay đổi tạo với 2 đầu đoạn OA cố định góc góc OIA = 90^o. Vậy I chuyển động trên đường tròn đường kính OA.

Chứng minh đảo: Lấy điểm I’ bất kỳ trên đường tròn đường kính AO. Đường thẳng AI’ cắt đường tròn (O) tại 2 điểm B’ và C’.

Ta chứng minh: I’B = I’C’.

Trong đường tròn đường kính AO ta có góc OI'A = 90^o (góc nội tiếp chắn nửa đường tròn)

OI'⊥ B'C'

I'B' = I'C' (đường kính vuông góc với dây cung)

Vậy quỹ tích các điểm I là trung điểm của dây BC của đường tròn tâm O khi BC quay xung quanh điểm A cố định là đường tròn đường kính AO.

Bài 3 trang 106 Sách bài tập Toán 9 Tập 2: 

Cho tam giác ABC có ba góc nhọn. Xác định vị trí của điểm M trong tam giác sao cho MA + MB + MC nhỏ nhất.

Lời giải:

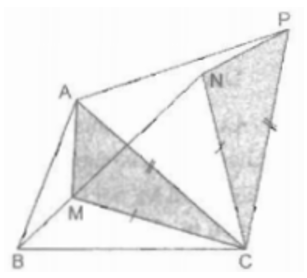
Trong ΔABC ta lấy điểm M. Nối MA, MB, MC.

Ta cần làm xuất hiện tổng MA + MB + MC sau đó tìm điều kiện để tổng đó nhỏ nhất.

Lấy MC làm cạnh dựng trên nửa mặt phẳng bờ BC chứa điểm A tam giác đều MCN. Suy ra: CM = MN.

Lấy AC làm cạnh dựng trên nửa mặt phẳng bờ AC không chứa điểm B tam giác đều APC. Khi đó, CA = CP

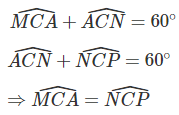
Xét ΔAMC và ΔPNC:

CM = CN (vì ΔMCN đều)

CA = CP (vì ΔAPC đều)

góc MCA = góc NCP (cmt)

Suy ra: ΔAMC = ΔPNC (c.g.c)

⇒ PN = AM

MA + MB + MC = NP + MB + MN

Ta có ΔABC cho trước nên điểm P cố định nên BM + MN + NP ngắn nhất khi 4 điểm B, M, N, P thẳng hàng.

Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích đầy đủ các môn được cập nhật liên tục tại chuyên trang của chúng tôi.

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải SBT Toán Hình 9 trang 105, 106: Bài 6: Cung chứa góc file Word, pdf hoàn toàn miễn phí!