Giải VBT Toán lớp 9 trang 5, 6, 7 Tập 1: Bài 1: Căn bậc hai

Giải vở bài tập Toán lớp 9 Tập 1 bài 1: Căn bậc hai được chúng tôi sưu tầm và đăng tải. Đây là lời giải kèm phương pháp giải hay các bài tập trong chương trình sách bài tập Toán 9. Là tài liệu tham khảo hữu ích dành cho các em học sinh và quý thầy cô giáo tham khảo và đối chiếu đáp án chính xác, chuẩn bị tốt cho việc tiếp thu, giảng dạy bài học mới đạt hiệu quả.

Giải Vở bài tập Toán lớp 9 Tập 1 Bài 1: Căn bậc hai

Bài 1 trang 5 Sách bài tập Toán 9 Tập 1: 

Tính căn bậc hai số học của:

a. 0,01     b. 0,04     c. 0,49     d. 0,64

e. 0,25     f. 0,81     g. 0,09     h. 0,16

Lời giải:

a. √0,01 = 0,1 vì 0,1 ≥ 0 và (0,1)² = 0,01

b. √0,04 = 0,2 vì 0,2 ≥ 0 và (0,2)² = 0,04

c. √0,49 = 0,7 vì 0,7 ≥ 0 và (0,7)² = 0,49

d. √0,64 = 0,8 vì 0,8 ≥ 0 và (0,8)² = 0,64

e. √0,25 = 0,5 vì 0,5 ≥ 0 và (0,5)² = 0,25

f. √0,81 = 0,9 vì 0,9 ≥ 0 và (0,9)² = 0,81

g. √0,09 = 0,3 vì 0,3 ≥ 0 và (0,3)² = 0,09

h. √0,16 = 0,4 vì 0,4 ≥ 0 và (0,4)² = 0,16

Bài 2 trang 5 Sách bài tập Toán 9 Tập 1: 

Dùng máy tính bỏ túi tim x thỏa mãn đẳng thức (làm tròn đến chữ số thập phân thứ ba).

a. x² = 5        b. x² = 6

c. x² = 2,5        d. x² = √5

Lời giải:

a. x² = 5 ⇒ x₁ = √5 hoặc x₂ = -√5

Ta có: x₁ = √5 ≈ 2,236 hoặc x₂ = -√5 ≈ -2,236

b. x² = 6 ⇒ x₁ = ≈6 hoặc x₂ = -≈6

Ta có: x₁ = 6 ≈ 2,449 hoặc x₂ = -≈6 ≈ -2,449

c. x² = 2,5 ⇒ x₁ = √2,5 hoặc x₂ = - √2,5

Ta có: x₁ = √2,5 ≈ 1,581 hoặc x₂ = - √2,5 = -1,581

d. x² = 5 ⇒ x₁ = √(√5) hoặc x₂ = √(√5)

Ta có: x₁ = √(√5) ≈ 1,495 hoặc x₂ = - √(√5) = -1,495.

Bài 3 trang 5 Sách bài tập Toán 9 Tập 1: 

Số nào có căn bậc hai là:

a. √5      b. 1,5      c. -0,1      d. -√9

Lời giải:

a. Số 5 có căn bậc hai là √5

b. Số 2,25 có căn bậc hai là 1,5

c. Số 0,01 có căn bậc hai là -0,1

d. Số 9 có căn bậc hai là -√9

Bài 4 trang 5 Sách bài tập Toán 9 Tập 1: 

Tìm x không âm biết:

a. √x = 3     b. √x = √5     c. √x = 0     d. √x = -2

Lời giải:

a. √x = 3 ⇒ x = 3² ⇒ x = 9

b. √x = √5 ⇒ x = (√5 )² ⇒ x = 5

c. √x = 0 ⇒ x = 0² ⇒ x = 0

d. Căn bậc hai số học là số không âm nên không tồn tại giá trị nào của √x thỏa mãn x = -2.

Bài 5 trang 6 Sách bài tập Toán 9 Tập 1: 

So sánh (không dùng bảng số hay máy tính bỏ túi)

a. 2 và √2 + 1     b. 1 và √3 – 1

c. 2√31 và 10     d. -√3.11 và -12

Lời giải:

a. Ta có: 1 < 2 ⇒ √1 < √2 ⇒ 1 < √2

Suy ra: 1 + 1 < √2 + 1

Vậy 2 < √2 + 1

b. Ta có: 4 > 3 ⇒ √4 > √3 ⇒ 2 > √3

Suy ra: 2 – 1 > √3 – 1

Vậy 1 > √3 – 1

c. Ta có: 31 > 25 ⇒ √31 > √25 ⇒ √31 > 5

Suy ra: 2.√31 > 2.5

Vậy 2.√31 > 10

d. Ta có: 11 < 16 ⇒ √11 < √16 ⇒ √11 < 4

Suy ra: -3.√11 > -3.4

Vậy -3√11 > -12

Bài 6 trang 6 Sách bài tập Toán 9 Tập 1: 

Tìm những khẳng định đúng trong các khẳng định sau:

a. Căn bậc hai của 0,36 là 0,6

b. Căn bậc hai của 0,36 là 0,06

c. √0,36 = 0,6

d. Căn bậc hai của 0,36 là 0,6 và -0,6

e. √0,36 = ± 0,6

Lời giải:

Câu a và c đúng.

Bài 7 trang 6 Sách bài tập Toán 9 Tập 1: 

Trong các số 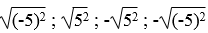 , số nào là căn bậc hai số học của 25?

Lời giải:

Căn bậc hai số học của 25 là .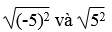

Bài 8 trang 6 Sách bài tập Toán 9 Tập 1: 

Chứng minh: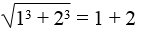 

Viết tiếp một số đẳng thức tương tự.

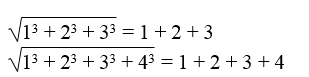
Lời giải:

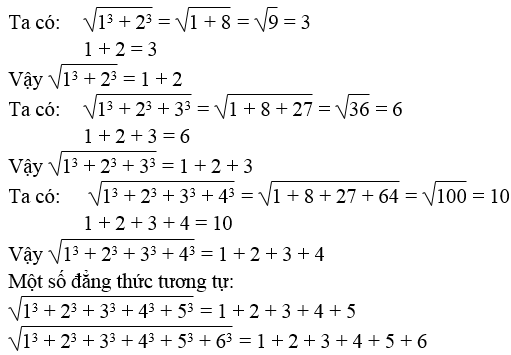
Bài 9 trang 6 Sách bài tập Toán 9 Tập 1: 

Cho hai số a, b không âm. Chứng minh:

a. Nếu √a < √b thì a < b

b. Nếu a < b thì √a < √b

Lời giải:

a. a ≥ 0; b ≥ 0 và a < b ⇒ b > 0

Ta có: √a ≥ 0; √b ≥ 0 suy ra: √a + √b > 0     (1)

Mặt khác: a – b = (√a )² – (√b )² = (√a + √b )(√a - √b )

Vì a < b nên a – b < 0

Suy ra: (√a + √b )(√a - √b ) < 0     (2)

Từ (1) và (2) suy ra: √a - √b < 0 ⇒ √a < √b

b. a ≥ 0; b ≥ 0 và √a < √b ⇒ √b > 0

Suy ra: √a + √b > 0 và √a - √b < 0

(√a + √b )(√a - √b ) < 0

⇒ (√a )² – (√b )² < 0 ⇒ a – b < 0 ⇒ a < b.

Bài 10 trang 6 Sách bài tập Toán 9 Tập 1: 

Cho số m dương. Chứng minh:

a. Nếu m > 1 thì √m > 1     b. Nếu m < 1 thì √m < 1

Lời giải:

a. Ta có: m > 1 ⇒ √m > √1 ⇒ √m > 1

b. Ta có: m < 1 ⇒ √m < √1 ⇒ √m < 1

Bài 11 trang 6 Sách bài tập Toán 9 Tập 1: 

Cho số m dương. Chứng minh:

a. Nếu m > 1 thì m > √m     b. Nếu m < 1 thì m < √m

Lời giải:

a. Ta có: m > 1 ⇒ √m > √1 ⇒ √m > 1

Vì m > 0 nên √m > 0

Suy ra: √m .√m > 1.√m ⇒ m > √m

b. Ta có: m < 1 ⇒ √m < √1 ⇒ √m < 1

Vì m > 0 nên √m > 0

Suy ra: √m .√m < 1.√m ⇒ m < √m.

Bài 1 trang 7 Sách bài tập Toán 9 Tập 1: 

Giá trị của √0,16 là

A. 0,04;

B. 0,4;

C. 0,04 và -0,04

D. 0,4 và -0,4.

Lời giải:

Chọn đáp án B.

Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích đầy đủ các môn được cập nhật liên tục tại chuyên trang của chúng tôi.

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Lời giải vở bài tập Toán lớp 9 Tập 1 trang 5, 6, 7: Bài 1: Căn bậc hai file Word, pdf hoàn toàn miễn phí!