Giải SBT Toán 9 trang 55, 56 Tập 2: Công thức nghiệm thu gọn

Giải bài tập sách bài tập Toán lớp 9: Bài 5: Công thức nghiệm thu gọn được chúng tôi sưu tầm và đăng tải. Đây là lời giải kèm phương pháp giải hay các bài tập trong chương trình Sách bài tập Toán 9. Là tài liệu tham khảo hữu ích dành cho các em học sinh và quý thầy cô giáo tham khảo và đối chiếu đáp án chính xác, chuẩn bị tốt cho việc tiếp thu, giảng dạy bài học mới đạt hiệu quả.

Bài 5: Công thức nghiệm thu gọn

Bài 27 trang 55 Sách bài tập Toán 9 Tập 2: 

Xác định a, b’,c trong mỗi phương trình rồi giải phương trình bằng công thức nghiệm thu gọn:

a. 5x² – 6x -1 = 0    

b. -3x² + 14x - 8 = 0

c. -7x² + 4x = 3    

d. 9x² + 6x + 1 = 0

Lời giải:

a. Phương trình 5x² – 6x -1 = 0 có hệ số a = 5, b’ = -3, c = -1

Ta có: Δ’ = b’² – ac = (-3)² -5.(-1) = 9 + 5 = 14 > 0

√Δ' =√14

Phương trình có hai nghiệm phân biệt :

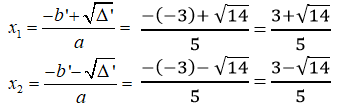
b. Phương trình -3x²+ 14x - 8 = 0 có hệ số a = -3, b’= 7, c = -8

Ta có: Δ' = b’² – ac = 7² – (-3).(-8) = 49 – 24 = 25 > 0

√Δ' = √25 = 5

Phương trình có 2 nghiệm phân biệt:

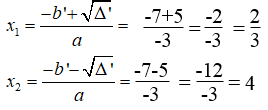
c. Phương trình -7x² +4x=3 ⇔ 7x² -4x+3 = 0 có hệ số a=7, b’=-2 , c=3

Ta có: Δ’ = b’² – ac = (-2)² -7.3 = 4- 21= -17 < 0

Vậy phương trình vô nghiệm

d. Phương trình 9x² +6x+1 =0 có hệ số a=9,b’=3,c=1

Ta có: Δ’ = b’² – ac = 3² -9.1 = 9 - 9 = 0

Phương trình có nghiệm kép:

x₁ = x₂ = -b'/a =-3/9 =-1/3

Bài 28 trang 55 Sách bài tập Toán 9 Tập 2: 

Với những giá trị nào của x thì giá trị của hai biểu thức sau bằng nhau?

a. x² +2 + 2√2 và 2(1+√2 )x

b. √3 x² + 2x -1 và 2√3 x +3

c. -2√2 x – 1 và √2 x² + 2x +3

d. x² - 2√3 x - √3 và 2x² +2x +√3

e. √3 x² + 2√5 x - 3√3 và -x² - 2√3 x +2√5 +1

Lời giải:

a. Ta có: x² +2 + 2√2 = 2(1 + √2)x ⇔ x² - 2(1 + √2)x + 2 + 2√2 = 0

Δ' = b’² – ac = [-(1 + √2)]²- 1(2 + 2√2)

= 1 + 2√2 +2 - 2 - 2√2 = 1 > 0

√Δ' = √1 = 1

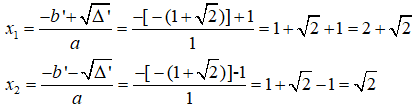
Vậy với x= 2 + √2 hoặc x = √2 thì giá trị của hai biểu thức trên bằng nhau

b. Ta có: √3 x² + 2x -1 = 2√3x + √3 ⇔ √3x² + 2x - 2√3x - 3 - 1 = 0

⇔ √3x² + (2 - 2√3 )x -4 =0 ⇔ √3x² + 2(1 - √3)x - 4 = 0

Δ' = b’² – ac= (1- √3 )² - √3(-4) = 1 - 2√3 + 3 + 4√3

= 1 + 2√3 + 3 = (1 + √3)² > 0

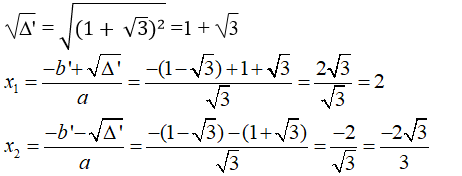
Vậy với x= 2 hoặc x = (-2√3)/3 thì giá trị của hai biểu thức trên bằng nhau

c. Ta có: -2√2x – 1 = √2x² + 2x + 3 ⇔ √2 x² + 2x + 3 + 2√2 x + 1= 0

⇔√2x² + 2(1 + √2)x + 4 = 0

Δ' = b’² – ac = (1+ √2)² - √2.4 = 1+2√2 + 2 - 4√2

= 1 - 2√2 + 2 = (√2 - 1)² > 0

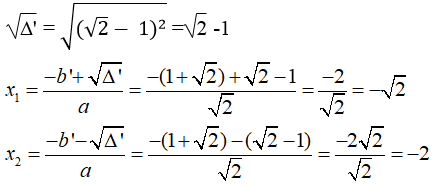
Vậy với x = -√2 hoặc x = -2 thì giá trị của hai biểu thức trên bằng nhau

d. Ta có: x² - 2√3x - √3 = 2x² + 2x + √3

⇔ x² - 2√3x - √3 - 2x² - 2x - √3 = 0

⇔ x² +2x +2√3x +2√3 = 0

⇔ x² + 2(1 +√3)x + 2√3 = 0

Δ' = b’² – ac = (1+ √3)² – 1.2√3 = 1 + 2√3 + 3 - 2√3 = 4 > 0

√Δ' = √4 = 2

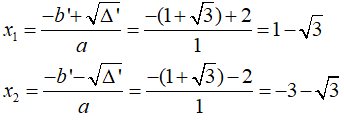
Vậy với x =1 - √3 hoặc x = - 3 - √3 thì giá trị của hai biểu thức trên bằng nhau

e.Ta có: √3x² + 2√5x - 3√3 = -x² - 2√3 x + 2√5 + 1

⇔ √3 x² + 2√5 x - 3√3 + x² + 2√3 x - 2√5 – 1 = 0

⇔ (√3 +1)x² + (2√5 + 2√3)x -3√3 - 2√5 – 1= 0

⇔ (√3 +1)x² + 2(√5 + √3)x - 3√3 - 2√5 – 1 = 0

Δ' = b’² – ac= (√3 + √5)² – (√3 +√1)(-3√3 - 2√5 – 1)

= 5 + 2√15 + 3 + 9 + 2√15 + √3 + 3√3 + 2√5 + 1

=18 + 4√15 + 4√3 + 2√5

= 1 + 12 + 5 + 2.2√3 + 2√5 + 2.2√3 .√5

= 1 + (2√3)² + (√5)² + 2.1.2√3 + 2.1.√5 + 2.2√3 .√5

= (1 +2√3 +√5)² > 0

Bài 29 trang 55 Sách bài tập Toán 9 Tập 2: 

Một vận động viên bơi lội nhảy cầu (xem hình dưới). Khi nhảy độ cao h từ người đó đến mặt nước (tính bằng mét ) phụ thuộc vào khoảng cách x từ điểm rơi đến chân cầu (tính bằng mét) bởi công thức : h = - (x - 1)² + 4. Hỏi khoảng cách x bằng bao nhiêu:

a. Khi vận động viên ở độ cao 3m?

b. Khi vận động viên chạm mặt nước?

Lời giải:

Khi vận động viên ở độ cao 3m nghĩa là h = 3m

Ta có: 3 = - (x – 1)² + 4 ⇔ (x – 1)² – 1=0 ⇔ x² – 2x = 0

⇔ x(x – 2) = 0 ⇔ x = 0 hoặc x – 2 = 0 ⇔ x = 0 hoặc x = 2

Vậy x = 0m hoặc x = 2m

Khi vận động viên chạm mặt nước nghĩa là h = 0m

Ta có: 0 = - (x – 1)² + 4 ⇔ x² -2x - 3 = 0

Δ' = b’² – ac = (-1)² -1.(-3) = 1 +3 = 4 > 0

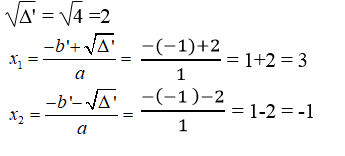
Vì khoảng cách không thể mang giá trị âm nên x = 3m.

Bài 30 trang 56 Sách bài tập Toán 9 Tập 2: 

Tính gần đúng nghiệm của phương trình (làm tròn đến chữ số thập phân thứ hai ):

a. 16x² – 8x + 1 = 0    

b. 6x² – 10x - 1 =0

c. 5x² + 24x + 9 = 0    

d. 16x² – 10x + 1 = 0

Lời giải:

a. 16x² – 8x + 1 = 0

Ta có: Δ' = (-4)² – 16.1 = 16 -16 = 0

Phương trình có nghiệm kép :

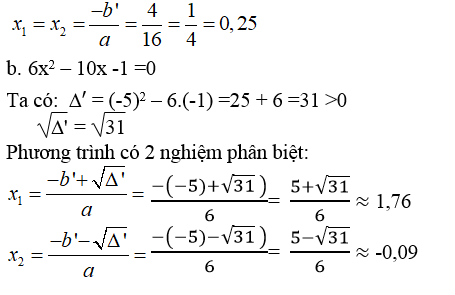
c. 5x² + 24x + 9 = 0

Ta có: Δ' = 12² - 5.9 = 144 - 45 = 99 > 0

√Δ' = √99 = 3√11

Phương trình có 2 nghiệm phân biệt:

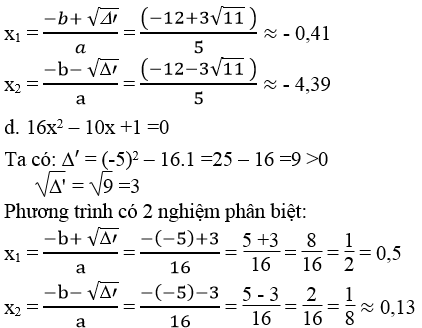
Bài 31 trang 56 Sách bài tập Toán 9 Tập 2: 

Với giá trị nào của x thì giá trị của hai hàm số bằng nhau?

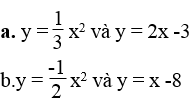
Lời giải:

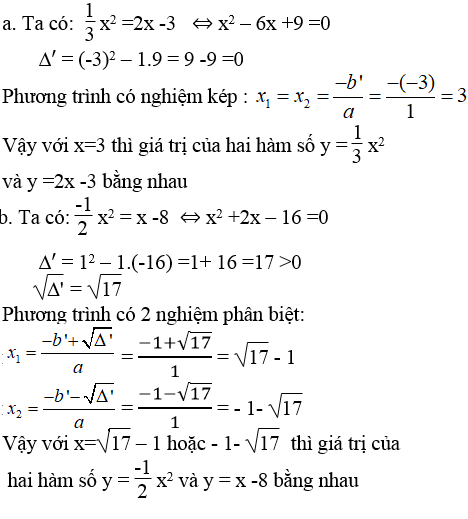
Bài 32 trang 56 Sách bài tập Toán 9 Tập 2: 

Với giá trị nào của m thì :

a. Phương trình 2x² – m²x + 18m = 0 có một nghiệm x = -3

b. Phương trình mx² – x – 5m² = 0 có một nghiệm x = -2

Lời giải:

a. Thay x=-3 vào phương trình 2x² – m²x +18m = 0 ta được:

2(-3)² - m²(-3) + 18m = 0 ⇔ 3m² +18m + 18 = 0

⇔ m² + 6m +6 = 0 (có hệ số a = 1, b = 6 nên b’ = 3; c = 6)

Δ' = 3² -1.6 = 9 - 6 = 3 > 0

√Δ' = √3

Phương trình có 2 nghiệm phân biệt:

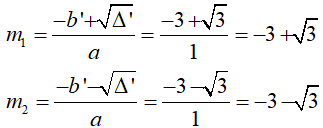
Vậy với m = -3 + √3 hoặc m = -3 - √3 thì phương trình đã cho có nghiệm x = -3

b. Thay x = -2 vào phương trình mx² – x – 5m² = 0 ta được:

m(-2)² – (-2) – 5m² = 0

⇔ - 5m² + 4m + 2 = 0

⇔ 5m² – 4m - 2 = 0 (Có a = 5; b = -4 nên b’ = - 2; c = - 2)

Δ' = (-2)² -5.(-2) = 4 + 10 = 14 > 0

√Δ' = √14

Phương trình có 2 nghiệm phân biệt:

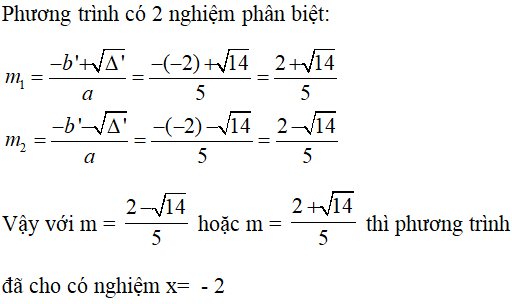
Bài 33 trang 56 Sách bài tập Toán 9 Tập 2: 

Với giá trị nào của m thì các phương trình sau có 2 nghiệm phân biệt

a. x² – 2(m+3)x + m² + 3 = 0

b. (m+1)x² + 4mx + 4m - 1 = 0

Lời giải:

a. x² – 2(m+3)x + m² + 3 = 0 (1)

Ta có: Δ' = [-(m+3)]² -1.(m² + 3) = m² + 6m + 9 – m² - 3

= 6m + 6

Phương trình (1) có 2 nghiệm phân biệt khi và chỉ khi:

Δ' > 0 ⇔ 6m + 6 > 0 ⇔ 6m > -6 ⇔ m > -1

Vậy m > -1 thì phương trình đã cho có 2 nghiệm phân biệt

b. (m + 1)x² + 4mx + 4m - 1 = 0     (2)

Ta có: Δ' = (2m)² – (m + 1)(4m - 1) = 4m² – 4m² + m – 4m +1

= 1 – 3m

Phương trình (2) có 2 nghiệm phân biệt khi và chỉ khi:

*m + 1 ≠ 0 ⇔ m ≠ -1

và *Δ' > 0 ⇔ 1 - 3m > 0 ⇔ 3m < 1 ⇔ m < 1/3

Vậy m < 1/3 và m ≠ -1 thì phương trình đã cho có 2 nghiệm phân biệt.

Bài 34 trang 56 Sách bài tập Toán 9 Tập 2: 

Với giá trị nào của m thì các phương trình sau có nghiệm kép

a. 5x² + 2mx – 2m + 15 = 0

b. mx² – 4(m -1)x - 8 = 0

Lời giải:

a. 5x² + 2mx – 2m + 15 = 0     (1)

Ta có: Δ' = m² – 5.(-2m + 15) = m² +10m - 75

Phương trình (1) có nghiệm kép khi và chỉ khi:

Δ' = 0 ⇔ m² + 10m – 75 = 0

Δ'm = 5² -1.(-75) = 25 + 75 = 100 > 0

√(Δ'm) = √100 =10

Phương trình có 2 nghiệm phân biệt:

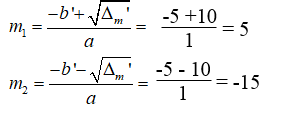
Vậy m = 5 hoặc m = -15 thì phương trình đã cho có nghiệm kép

b. mx² – 4(m -1)x - 8 = 0     (2)

Phương trình (2) có nghiệm kép khi và chỉ khi: m≠ 0 và Δ'=0

Ta có: Δ' = [-2(m - 1)]² – m(-8) = 4(m² -2m +1) + 8m

=4m² – 8m + 4 + 8m = 4m² + 4

Vì 4m² + 4 luôn luôn lớn hơn 0 nên Δ' không thể bằng 0 .Vậy không có giá trị nào của m để phương trình có nghiệm kép.

Bài tập bổ sung (trang 56)

Bài 1 trang 56 Sách bài tập Toán 9 Tập 2: 

Giả sử x₁, x₂ là hai nghiệm của phương trình bậc hai ax² + bx + c = 0 có ∆’ = 0. Điều nào sau đây là đúng?

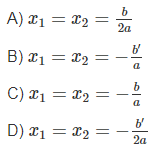
Lời giải:

Giả sử x₁, x₂ là hai nghiệm của phương trình bậc hai ax² + bx + c = 0 có ∆’ = 0

Do đó, phương trình có nghiệm kép x₁ = x₂ = -b'/a

Chọn B

Bài 2 trang 56 Sách bài tập Toán 9 Tập 2: 

Tìm mối liên hệ giữa a, b, c để phương trình (b² + c²)x² - 2acx + a² - b² = 0 có nghiệm.

Lời giải:

Hoặc b ≠ 0 hoặc c ≠ 0 phương trình có :

Bài 3 trang 56 Sách bài tập Toán 9 Tập 2: 

Chứng tỏ rằng phương trình (x - a)(x - b) + (x - b)(x - c) + (x - c)(x - a) = 0 luôn có nghiệm

Lời giải:

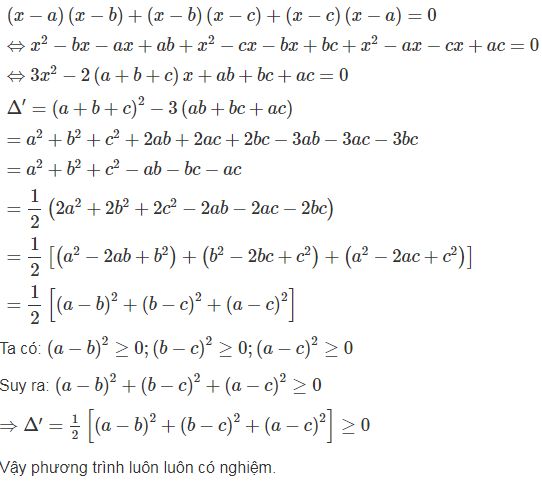
Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích đầy đủ các môn được cập nhật liên tục tại chuyên trang của chúng tôi.

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải SBT Toán 9 trang 55, 56: Bài 5: Công thức nghiệm thu gọn file Word, pdf hoàn toàn miễn phí!