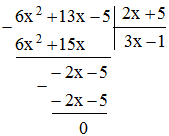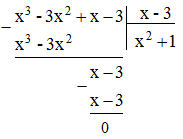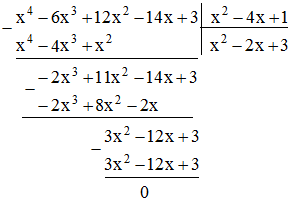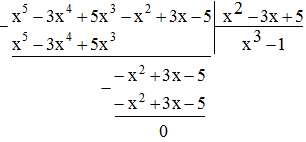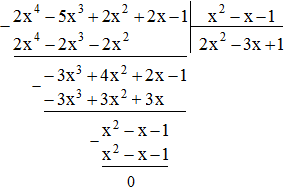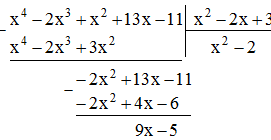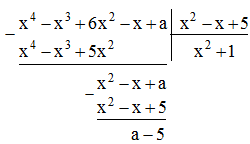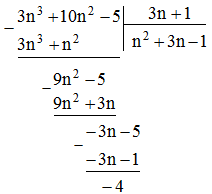Giải SBT Toán 8 trang 13 tập 1 bài 12: Chia đa thức một biến đã sắp xếp

Lời giải sách bài tập Toán 8 tập 1 bài 12: Chia đa thức một biến đã sắp xếp được giải đáp chi tiết và rõ ràng nhất, giúp cho các bạn học sinh có thể tham khảo và chuẩn bị tốt nhất cho bài học sắp tới nhé.

Giải bài 48 trang 13 SBT Toán lớp 8 tập 1

Làm tính chia:

a. (6x² + 13x – 5) : (2x + 5)

b. (x³ – 3x² + x – 3) : (x – 3)

c. (2x⁴ + x³ – 5x² – 3x – 3) : (x² – 3)

Lời giải:

a.

b.

c.

Giải bài 49 trang 13 SBT lớp 8 Toán tập 1

Sắp xếp các đa thức sau theo lũy thừa giảm của biến rồi thực hiện phép chia:

a. (12x² – 14x + 3 – 6x³ + x⁴) : (1 – 4x + x²)

b. (x⁵ – x² – 3x⁴ + 3x + 5x³ – 5) : (5 + x² – 3x)

c. (2x² – 5x³ + 2x + 2x⁴ – 1) : (x² – x – 1)

Lời giải:

a.

b.

c.

Giải bài 50 trang 13 Toán lớp 8 SBT tập 1

Cho hai đa thức A = x⁴ – 2x³ + x² + 13x -11 và B = x² – 2x + 3. Tìm thương Q và số dư R sao cho A = B.Q + R.

Lời giải:

Thương Q = x² – 2

Dư R = 9x – 5

Ta thấy x⁴ – 2x³ + x² + 13x - 11 = (x² – 2x + 3)( x² – 2) + (9x – 5)

Vậy A = B.Q + R

Giải bài 51 trang 13 tập 1 SBT Toán lớp 8

Tìm a để đa thức x⁴ – x³ + 6x² - x + a chia hết cho đa thức x² – x + 5

Lời giải:

Để có phép chia hết thì số dư phải bằng 0.

Ta có: a – 5 = 0 hay a = 5.

Giải bài 52 trang 13 SBT Toán tập 1 lớp 8

Tìm giá trị nguyên của n để giá trị biểu thức 3n³ + 10n² – 5 chia hết cho giá trị của biểu thức 3n + 1.

Lời giải:

Ta có: 3n³ + 10n² – 5 = (3n + 1)(n² + 3n – 1) – 4

Để phép chia đó là chia hết thì 4 ⋮ 3n + 1⇒ 3n + 1 ∈ Ư(4)

       3n + 1 ∈ {-4; -2; -1; 1; 2; 4}

       3n + 1 = -4⇒ 3n = -5⇒ n = 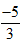 ∉ Z : loại

       3n + 1 = -2⇒ 3n = -3⇒ n = -1 ∈ Z

       3n + 1 = -1⇒ 3n = -2⇒ n = 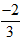 ∉ Z : loại

       3n + 1 = 1⇒ 3n = 0⇒ n = 0 ∈ Z

       3n + 1 = 2⇒ 3n = 2⇒ n = 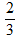 ∉ Z : loại

       3n + 1 = 4⇒ 3n = 3⇒ n = 1 ∈ Z

Vậy n ∈ {-1; 0; 1} thì 3n³ + 10n² – 5 chia hết cho 3n + 1.

►► CLICK NGAY vào nút TẢI VỀ dưới đây để download Giải sách bài tập Toán lớp 8 tập 1 trang 13 bài 12 file word, pdf hoàn toàn miễn phí.