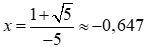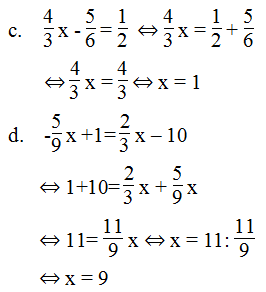Giải SBT Toán 8 trang 6, 7 tập 2 Bài 2 chi tiết nhất

Lời giải Sách bài tập Toán lớp 8 tập 2 trang 6, 7: Bài 2: Phương trình bậc nhất một ẩn và cách giải gồm các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải bài 10 SBT Toán lớp 8 tập 2 trang 6

Bằng quy tắc chuyển vế, giải các phương trình sau:

a. x – 2,25 = 0,75

b. 19,3 = 12 – x

c. 4,2 = x + 2,1

d. 3,7 – x = 4

Lời giải:

a. x – 2,25 = 0,75 ⇔ x = 0,75 + 2,25 ⇔ x = 3

b. 19,3 = 12 – x ⇔ x = 12 – 19,3 ⇔ x = - 7,3

c. 4,2 = x + 2,1 ⇔ x = 4,2 – 2,1 ⇔ x = 2,1

d. 3,7 – x = 4 ⇔ 3,7 – 4 = x ⇔ x = - 0,3

Giải bài 11 trang 6 SBT lớp 8 Toán tập 2

Bằng quy tắc nhân, tìm giá trị gần đúng nghiệm của các phương trình sau (làm tròn đến chữ số thập phân thứ ba).

a. 2x = √13

b. –5x = 1 + √5

c. x√2 = 4√3

Lời giải:

a. 2x = √13 ⇔ x = √13/2 ⇔ x ≈ 1,803

b. – 5x = 1 + √5 ⇔ 

c. x√2 = 4√3 ⇔ x = 4√3 / √2 ⇔ x ≈ 4,899

Giải bài 12 Toán lớp 8 SBT trang 6 tập 2

Tìm giá trị của m sao cho phương trình sau đây nhận x = -2 là nghiệm: 2x + m = x – 1

Lời giải:

Thay x = -2 vào hai vế của phương trình, ta có:

2.(-2) + m = - 2 – 1 ⇔ -4 + m = -3 ⇔ m = 1

Vậy với m = 1 thì phương trình 2x + m = x – 1 nhận x = -2 là nghiệm.

Giải bài 13 trang 7 tập 2 SBT Toán lớp 8

Tìm giá trị của k, biết rắng một trong hai phương trình sau đây nhận x = 5 là nghiệm, phương trình còn lại nhận x = -1 là nghiệm: 2x = 10 và 3 – kx = 2

Lời giải:

Thay x = 5 vào vế trái của phương trình 2x = 10, ta thấy giá trị của hai vế bằng nhau. Vậy x = 5 là nghiệm của phương trình 2x = 10.

Khi đó x = -1 là nghiệm của phương trình 3 – kx = 2.

Thay x = -1 vào phương trình 3 – kx = 2, ta có:

3 – k(-1) = 2 ⇔ 3 + k = 2 ⇔ k = -1

Vậy k = -1.

Giải bài 14 SBT Toán trang 7 tập 2 lớp 8

Giải các phương trình sau:

a. 7x + 21 = 0

b. 5x – 2 = 0

c. 12 – 6x = 0

d. -2x + 14 = 0

Lời giải:

a. 7x + 21 = 0 ⇔ 7x = -21 ⇔ x = -3

b. 5x – 2 = 0 ⇔ 5x = 2 ⇔ x = 2/5

c. 12 – 6x = 0 ⇔ 12 = 6x ⇔ x = 2

d. -2x + 14 = 0 ⇔ -2x = -14 ⇔ x = 7

Giải bài 15 Toán SBT lớp 8 trang 7 tập 2

Giải các phương trình sau:

a. 0,25x + 1,5 = 0

b. 6,36 – 5,3x = 0

c. 4/3 x - 5/6 = 1/2

d. -5/9 x + 1 = 2/3 x – 10

Lời giải:

a. 0,25x + 1,5 = 0 ⇔ 0,25x = -1,5 ⇔ x = -6

b. 6,36 – 5,3x = 0 ⇔ 6,36 = 5,3x ⇔ x = 1,2

Giải bài 16 lớp 8 SBT Toán tập 2 trang 7

Giải các phương trình sau:

a. 3x + 1 = 7x – 11

b. 5 – 3x = 6x + 7

c. 11 – 2x = x – 1

d. 15 – 8x = 9 – 5x

Lời giải:

a. 3x + 1 = 7x – 11 ⇔ 3x – 7x = -11 – 1 ⇔ -4x = -12 ⇔ x = 3

b. 5 – 3x = 6x + 7 ⇔ 5 – 7 = 6x + 3x ⇔ -2 = 9x ⇔ x = -2/9

c. 11 – 2x = x – 1 ⇔ 11 + 1 = x + 2x ⇔ 12 = 3x ⇔ x = 4

d. 15 – 8x = 9 – 5x ⇔ -8x + 5x = 9 – 15 ⇔ -3x = -6 ⇔ x = 2

Giải bài 17 trang 7 Toán tập 2 lớp 8 SBT

Chứng tỏ rằng các phương trình sau đây vô nghiệm:

a. 2(x + 1) = 3 + 2x

b. 2(1 – 1,5x) + 3x = 0

c. |x| = -1

Lời giải:

a. Ta có: 2(x + 1) = 3 + 2x ⇔ 2x + 2 = 3 + 2x ⇔ 0x = 1

Vậy phương trình vô nghiệm.

b. Ta có: 2(1 – 1,5x) + 3x = 0 ⇔ 2 – 3x + 3x = 0 ⇔ 2 + 0x = 0

Vậy phương trình vô nghiệm.

c. Vì |x| ≥ 0 nên phương trình |x| = -1 vô nghiệm.

Giải bài 18 SBT Toán tập 2 lớp 8 trang 7

Cho phương trình (m² – 4)x + 2 = m. Giải phương trình trong mỗi trường hợp sau:

a. m = 2

b. m = -2

c. m = -2,2

Lời giải:

a. Khi m = 2, phương trình đã cho trở thành:

(2² – 4)x + 2 = 2 ⇔ 0x + 2 = 2 ⇔ 2 = 2

Vậy phương trình đã cho có vô số nghiệm.

b. Khi m = -2, phương trình đac cho trở thành:

[(-2)² – 4]x + 2 = -2 ⇔ 0x + 2 = -2 ⇔ 0x = -4

Vậy phương trình đã cho vô nghiệm.

c. Khi m = -2,2, phương trình đã cho trở thành:

[(-2,2)² – 4]x + 2 = -2,2 ⇔ 0,84x + 2 = -2,2

⇔ 0,84x = -2,2 – 2 ⇔ 0,84x = -4,2 ⇔ x = -5

Vậy phương trình đã cho có nghiệm x = -5.

►► CLICK NGAY vào TẢI VỀ dưới đây để download hướng dẫn giải Sách bài tập Toán lớp 8 tập 2 trang 6, 7 file word, pdf hoàn toàn miễn phí.