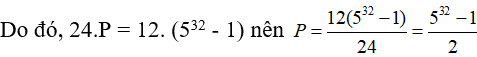Giải SBT toán lớp 8 trang 7, 8 tập 1: Hằng đẳng thức đáng nhớ

Giải bài tập Sách bài tập Toán 8 tập 1 bài 3, 4, 5: Hằng đẳng thức đáng nhớ được tổng hợp và chọn lọc kỹ lưỡng. Dưới đây là lời giải chi tiết cho các câu hỏi trong sách bài tập nằm trong khung chương trình giảng dạy môn Toán lớp 8 tập 1. Hi vọng rằng đây sẽ là những tài liệu bổ ích trong công tác giảng dạy và học tập của quý thầy cô cùng các em học sinh.

Bài 11 trang 7 SBT Toán lớp 8 tập 1

 Tính:

a, (x + 2y)²

b, (x – 3y)(x + 3y)

c, (5 – x)²

Lời giải:

a, (x + 2y)² = x² + 4xy + 4y²

b, (x – 3y)(x + 3y) = x² – (3y)² = x² – 9y²

c, (5 – x)2 = 5² – 10x + x² = 25 – 10x + x²

Bài 12 SBT Toán trang 7 lớp 8 tập 1

Tính:

a, (x – 1)²

b, (3 – y)²

c, (x - 1/2)²

Lời giải:

a, (x – 1)² = x² –2x + 1

b, (3 – y)² = 9 – 6y + y²

c, (x - 1/2)² = x² – x + 1/4

Bài 13 SBT Toán lớp 8 trang 7 tập 1

Viết các biểu thức sau dưới dạng bình phương một tổng:

a, x² + 6x + 9

b, x² + x + 1/4

c,2xy² + x²y⁴ + 1

Lời giải:

a, x² + 6x + 9 = x² + 2.x.3 + 3² = (x + 3)²

b, x² + x + 1/4 = x² + 2.x.1/2 + (1/2 )² = (x + 1/2)²

c, 2xy² + x²y⁴ + 1 = (xy²)² + 2.xy².1 + 1² = (xy² + 1)²

Bài 14 SBT Toán tập 1 lớp 8 trang 7

Rút gọn biểu thức:

a, (x + y)² + (x – y)²

b, 2(x – y)(x + y) + (x + y)² + (x – y)²

c, (x – y + z)² + (z – y)² + 2(x – y + z)(y – z)

Lời giải:

a, (x + y)² + (x – y)²

= x² + 2xy + y² + x² – 2xy + y²

= 2x² + 2y²

b, 2(x – y)(x + y) + (x + y)² + (x – y)²

= [(x + y) + (x – y)]² = (2x)² = 4x²

c, (x – y + z)² + (z – y)² + 2(x – y + z)(y – z)

= (x – y + z)² + 2(x – y + z)(y – z) + (y – z)²

= [(x – y + z) + (y – z)]² = x²

Bài 15 Toán lớp 8 SBT tập 1 trang 7

Biết số tự nhiên a chia cho 5 dư 4. Chứng minh rằng a2 chia cho 5 dư 1.

Lời giải:

Số tự nhiên a chia cho 5 dư 4, ta có: a = 5k + 4 (k ∈N)

Ta có: a² = (5k + 4)²

= 25k² + 40k + 16

= 25k² + 40k + 15 + 1

= 5(5k² + 8k +3) +1

Ta có: 5(5k² + 8k + 3) ⋮ 5

Vậy a² = (5k + 4)² chia cho 5 dư 1.

Bài 16 Toán lớp 8 SBT tập 1 trang 7

Tính giá trị của biểu thức sau:

a, x² – y² tại x = 87 và y = 13

b, x³ – 3x² + 3x – 1 tại x = 101

c, x³ + 9x²+ 27x + 27 tại x = 97

Lời giải:

a, Ta có: x² – y² = (x + y)(x – y)

b, Thay x = 87, y = 13, ta được:

x² – y² = (x + y)(x – y)

= (87 + 13)(87 – 13)

= 100.74 = 7400

c, Ta có: x³ + 9x² + 27x + 27

= x³ + 3.x².3 + 3.x.3² + 3³

= (x + 3)³

Thay x = 97, ta được: (x + 3)³ = (97 + 3)³ = 100³ = 1000000

Bài 17 Toán lớp 8 trang 7 SBT tập 1)

Chứng minh rằng:

a, (a + b)(a² – ab + b²) + (a – b)(a² + ab + b²) = 2a³

b, (a + b)[(a – b)² + ab] = (a + b)[a² – 2ab + b² + ab] = a³ + b³

c, (a² + b²)(c² + d²) = (ac + bd)² + (ad – bc)²

Lời giải:

a, Ta có: (a + b)(a² – ab + b²) + (a – b)(a² + ab + b²) = a³ + b³ + a³ – b³ = 2a³

Vế trái bằng vế phải nên đẳng thức được chứng minh.

b, Ta có: (a + b)[(a – b)² + ab] = (a + b)[a² – 2ab + b² + ab]

= (a + b)(a² – 2ab + b²) = a³ + b³

Vế phải bằng vế trái nên đẳng thức được chứng minh.

c, Ta có: (ac + bd)² + (ad – bc)²

= a²c² + 2abcd + b²d² + a²d² – 2abcd + b²c²

= a²c² + b²d² + a²d² + b²c² = c²(a² + b²) + d²(a² + b²)

= (a² + b²)(c² + d²)

Vế phải bằng vế trái nên đẳng thức được chứng minh.

Bài 18 Toán SBT tập 1 lớp 8 trang 7

Chứng tỏ rằng:

a, x² – 6x + 10 > 0 với mọi x

b, 4x – x² – 5 < 0 với mọi x

Lời giải:

a, Ta có: x² – 6x + 10 = x² – 2.x.3 + 9 + 1 = (x – 3)² + 1

Vì (x – 3)² ≥ 0 với mọi x nên (x – 3)² + 1 > 0 mọi x

Vậy x² – 6x + 10 > 0 với mọi x.

b, Ta có: 4x – x2 – 5 = -(x² – 4x + 4) – 1 = -(x – 2)² -1

Vì (x – 2)² ≥ 0 với mọi x nên –(x – 2)² ≤ 0 với mọi x.

Suy ra: -(x – 2)² -1 ≤ 0 với mọi x

Vậy 4x – x2 – 5 < 0 với mọi x.

Bài 19 trang 7 SBT Toán tập 1 lớp 8

Tìm giá trị nhỏ nhất của các đa thức:

a, P = x² – 2x + 5

b, Q = 2x² – 6x

c, M = x² + y² – x + 6y + 10

Lời giải:

a, Ta có: P = x² – 2x + 5 = x² – 2x + 1 + 4 = (x – 1)² + 4

Vì (x – 1)² ≥ 0 nên (x – 1)² + 4 ≥ 4

Suy ra: P = 4 là giá trị bé nhất ⇒ (x – 1)2 = 0 ⇒ x = 1

Vậy P = 4 là giá trị bé nhất của đa thức khi x = 1.

b, Ta có: Q = 2x² – 6x = 2(x² – 3x) = 2(x² – 2.3/2 x + 9/4 - 9/4 )

= 2[(x - 2/3 ) - 9/4 ] = 2(x - 2/3 )² - 9/²

Vì (x - 2/3 )² ≥ 0 nên 2(x - 2/3 )² ≥ 0 ⇒ 2(x - 2/3 )2 - 9/2 ≥ - 9/2

Suy ra: Q = - 9/2 là giá trị nhỏ nhất ⇒ (x - 2/3 )² = 0 ⇒ x = 2/3

Vậy Q = - 9/2 là giá trị nhỏ nhất của đa thức khi x = 2/3 .

c, Ta có: M = x² + y² – x + 6y + 10 = (y² + 6y + 9) + (x² – x + 1)

= (y + 3)² + (x² – 2.1/2 x + 1/4 + 3/4) = (y + 3)² + (x - 1/2)² + 3/4

Vì (y + 3)² ≥ 0 và (x - 1/2)² ≥ 0 nên (y + 3)² + (x - 1/2)² ≥ 0

⇒ (y + 3)² + (x - 12)² + 3/4 ≥ 3/4

⇒ M = 3/4 là giá trị nhỏ nhất khi (y + 3)² =0

⇒ y = -3 và (x - 1/2)² = 0 ⇒ x = 1/2

Vậy M = 3/4 là giá trị nhỏ nhất tại y = -3 và x = 1/2

Bài 20 SBT tập 1 Toán lớp 8 trang 7

Tìm giá trị lớn nhất của đa thức:

a, A = 4x – x² + 3

b, B = x – x²

c, N = 2x – 2x² – 5

Lời giải:

a, Ta có: A = 4x – x² + 3

= 7 – x² + 4x – 4

= 7 – (x² – 4x + 4)

= 7 – (x – 2)²

Vì (x – 2)² ≥ 0 nên A = 7 – (x – 2)² ≤ 7

Vậy giá trị của A lớn nhất là 7 tại x = 2

b, Ta có: B = x – x²

= 1/4 - x² + x - 1/4

= 1/4 - (x² – 2.x. 1/2 + 1/4)

= 1/4 - (x - 1/2)²

Vì (x - 1/2)² ≥ 0 nên B = 1/4 - (x - 1/2)² ≤ 1/4

Vậy giá trị lớn nhất của B là 1/4 tại x = 1/2 .

c, Ta có: N = 2x – 2x² – 5

= - 2(x² – x + 5/2)

= - 2(x² – 2.x. 1/2 + 1/4 + 9/4)

= - 2[(x - 1/2)² + 9/4 ]

= - 2(x - 1/2)² - 9/2

Vì (x - 1/2 )² ≥ 0 nên - 2(x - 1/2)² ≤ 0

Suy ra: N = - 2(x - 1/2)² - 9/2 ≤ - 9/2

Vậy giá trị lớn nhất của biểu thức N là - 9/2 tại x = 1/2 

Bài tập bổ sung 3.1 trang 8 SBT Toán 8 Tập 1

Cho x² + y² = 26 và xy = 5, giá trị của (x-y)² là:

A. 4

B. 16

C. 21

D. 36

Lời giải:

Chọn B

Ta có: (x-y)² = x²-2xy+y² = (x²+y²) - 2xy = 26 - 2.5=16

Bài tập bổ sung 3.2 SBT Toán lớp 8 trang 8 Tập 1

Kết quả của tích (a² + 2a + 4)(a − 2) là:

A. (a+2)³ B. (a-2)³ C. a³ + 8 D. a³ − 8

Lời giải:

Chọn D.

Cách 1: (a² + 2a + 4)(a − 2)=a³-2a²+2a²-4a+4a-8=a³ – 8

Cách 2: (a² + 2a + 4)(a − 2) = (a- 2).(a² + 2a + 4) = a³ – 8 ( hằng đẳng thức).

Bài tập bổ sung 3.3 SBT Toán lớp 8 Tập 1 trang 8

Rút gọn các biểu thức:

a) P = (5x − 1) + 2(1 − 5x)(4 + 5x) + (5x+4) ²

b) Q = (x-y) ³ + (y+x) ³ + (y-x) ³ – 3xy(x + y)

Lời giải:

a. P = (5x − 1) + 2(1 − 5x)(4 + 5x) + (5x + 4) ²

      = 5x – 1 + (2 – 10x).( 4+ 5x) + ( 5x + 4)²

      = 5x – 1 + 8 + 10x – 40x – 50x² + 25x² + 40x + 16

      = (- 50x² + 25x²)+ ( 5x + 10x – 40x + 40x) + (- 1+ 8 + 16)

      = -25x² + 15x + 23

b. Q = (x-y) ³ + (y+x)³ + (y-x)³ – 3xy(x + y)

      = x³ – 3x²y + 3xy² – y³ + y³ + 3y².x + 3yx² + x³ + y³ – 3y².x +3yx² – x³ – 3x²y – 3xy²

      = x³ – 3x²y + 3xy² – y³ + y³ + 3.xy² + 3x².y + x³ + y³ – 3x.y²+ 3x².y – x³ – 3x²y – 3xy²

       = ( x³ + x³ – x³)+ ( - 3x²y + 3x²y+ 3x²y – 3x²y)+ (3xy² + 3xy² - 3xy²- 3xy²) + (-y³+ y³+ y³ )

       = x³ + 0x²y + 0.xy² + y³

       = x³+ y³

Bài tập bổ sung 3.4 Toán lớp 8 Tập 1 trang 8 SBT

Rút gọn biểu thức:

P = 12.(5² + 1)(5⁴ + 1)(5⁸ + 1)(5¹⁶ + 1)

Lời giải:

Ta có:

(5² - 1).P = ( 5² – 1).12.(5² + 1)(5⁴ + 1)(5⁸ + 1)(5¹⁶ + 1)

= 12.( 5² – 1).(5² + 1)(5⁴ + 1)(5⁸ + 1)(5¹⁶ + 1)

= 12.( 5⁴ - 1)( 5⁴ + 1)( 5⁸ + 1)(5¹⁶ + 1)

= 12.( 5⁸ - 1)( 5⁸ + 1)(5¹⁶ + 1)

= 12.( 5¹⁶ - 1)(5¹⁶ + 1)

= 12.( 5³² - 1)

Bài tập bổ sung 3.5 trang 8 SBT Toán lớp 8 Tập 1

Chứng minh hằng đẳng thức:

(a+b+c)³= a³ + b³ + c³ + 3(a+b)(b+c)(c+a)

Lời giải:

Biến đổi vế trái:

(a+b+c)³= [(a+b)+c]³ = (a+b)³+3(a+b)² c+3(a+b)c²+c³

      = a³ + 3a²b + 3ab² + b³ + 3(a² + 2ab + b²)c + 3ac² + 3bc² + c³

      = a³ + 3a²b + 3ab² + b³ + 3a²c + 6abc + 3b²c + 3ac² + 3bc² + c³

      = a³ + b³ + c³ + 3a²b + 3ab² + 3a²c + 6abc + 3b²c + 3ac² + 3bc²

      = a³ + b³ + c³ + (3a²b + 3ab²) +( 3a²c + 3abc)+ (3abc + 3b²c)+(3ac² + 3bc²)

      = a³ + b³ + c³ + 3ab(a + b) + 3ac(a + b) + 3bc(a + b) + 3c²(a + b)

      = a³ + b³ + c³ + 3(a + b)(ab + ac + bc + c²)

      = a³ + b³ + c³ + 3(a + b)[a(b + c) + c(b + c)]

      = a³ + b³ + c³ + 3(a + b)(b + c)(a + c) (đpcm)

 

CLICK NGAY vào TẢI VỀ dưới đây để download Giải toán lớp 8 SBT tập 1 trang 7, 8 bài  3, 4, 5: Những hằng đẳng thức đáng nhớ file word, pdf hoàn toàn miễn phí.