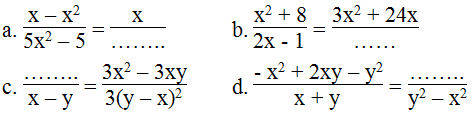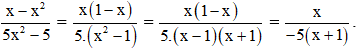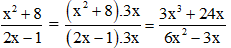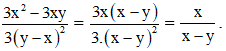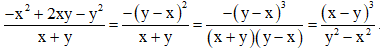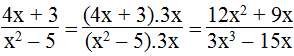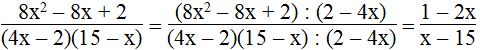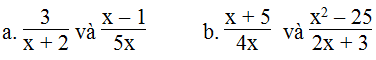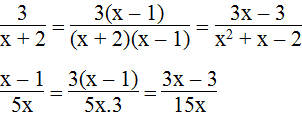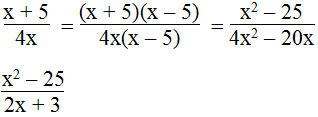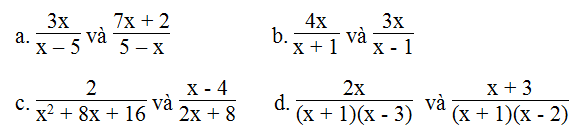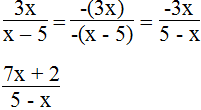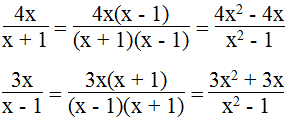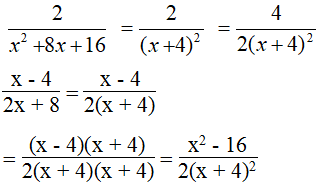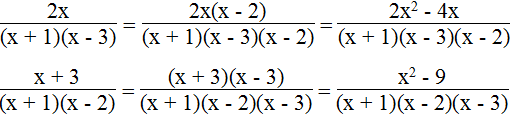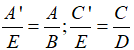Giải SBT Toán 8 trang 25 tập 1 bài 2: Tính chất cơ bản của phân thức

Giải sách bài tập Toán 8 trang 25 tập 1 bài 2: Tính chất cơ bản của phân thức được giải đáp chi tiết và rõ ràng nhất, giúp cho các bạn học sinh có thể tham khảo và chuẩn bị tốt nhất cho bài học sắp tới nhé.

Giải bài 4 trang 25 SBT Toán tập 1 lớp 8

Dùng tính chất cơ bản của phân thức, hãy điền một đa thức thích hợp vào các chỗ vào các chỗ trống trong mỗi đẳng thức sau:

Lời giải:

a. Ta có: x – x² = x.(1 – x)

(Tử thức của phân thức bên phải bằng tử thức của phân thức bên trái chia cho (1 – x).

Do đó ta chia cả tử và mẫu của phân thức bên trái cho 1 – x thì thu được phân thức bên phải.)

Vậy đa thức cần điền là -5x – 5.

b. 3x³ + 24x = 3x.(x² + 8).

(Tử thức của phân thức bên phải bằng tử thức của phân thức bên trái nhân với 3x.

Do đó ta nhân cả tử và mẫu của phân thức bên trái với 3x thì thu được phân thức bên phải)

Vậy đa thức cần điền là 6x² – 3x.

c. 3(y – x)² = 3.(x – y)² = (x – y).3(x – y)

(Mẫu thức của phân thức bên trái bằng mẫu thức của phân thức bên phải chia cho 3(x – y)

Do đó ta chia cả tử và mẫu của phân thức bên phải cho 3(x – y) để thu được phân thức bên trái)

Vậy đa thức cần điền là x.

d. y² – x² = (y – x)(y + x)

(Mẫu thức của phân thức bên phải bằng mẫu thức của phân thức bên trái nhân với (y – x).

Do đó ta nhân cả tử và mẫu của phân thức bên trái với (y – x) để thu được phân thức bên phải)

Vậy đa thức cần điền là (x – y)³.

Giải bài 5 trang 25 tập 1 SBT Toán lớp 8

Biến đổi mỗi phân thức sau thành một phân thức bằng nó có từ là đa thức A cho trước:

a. 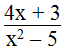 , A = 12x² + 9x

b. 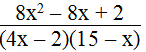, A = 1 – 2x

Lời giải:

a. A = 12x² + 9x = 3x(4x + 3)

Suy ra: 

b. A = 1 – 2x ⇒ (8x² – 8x + 2) : (1 – 2x) = 2 – 4x

Suy ra: 

Giải bài 6 trang 25 Toán lớp 8 SBT tập 1

Dùng tính chất cơ bản của phân thức để biến đổi mỗi cặp phân thức sau thành cặp phân thức bằng nó và có cùng tử thức:

Lời giải:

a.

b. Ta có: x² – 25 = (x – 5). (x+ 5).

Giải bài 7 trang 25 SBT lớp 8 Toán tập 1

Dùng tính chất cơ bản của phân thức hoặc quy tắc đổi dấu để biến đổi mỗi cặp phân thức sau thành cặp phân thức bằng nó và có cùng mẫu thức:

Lời giải:

a.

b.

c.

d.

Giải bài 8 trang 25 SBT Toán lớp 8 tập 1

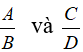
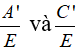
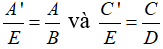
Cho hai phân thức . Chứng minh rằng có vô số cặp phân thức cùng mẫu,có dạng  thỏa mãn điều kiện .

Lời giải:

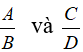
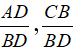
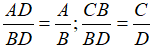
Với hai phân thức ,ta tìm được hai phân thức cùng mẫu  , và thỏa mãn điều kiện :

.

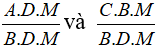
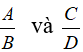
Ta nhân tử và mẫu của hai phân thức đó với cùng một đa thức M ≠ 0 bất kỳ, ta có hai phân thức mới cùng mẫu  và lần lượt bằng hai phân thức .

Đặt B.D.M = E, A.D.M = A', C.B.M = C' ta có:

Vì có vô số đa thức M ≠ 0 nên ta có vô số phân thức cùng mẫu bằng hai phân thức đã cho.

►► CLICK NGAY vào nút TẢI VỀ dưới đây để download Giải sách bài tập Toán lớp 8 tập 1 trang 25 file word, pdf hoàn toàn miễn phí.