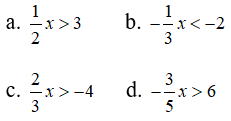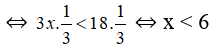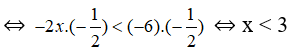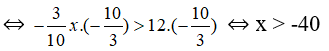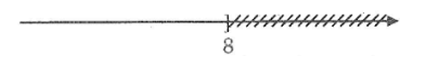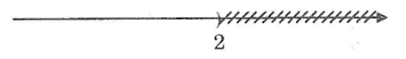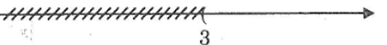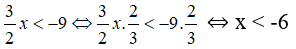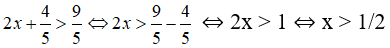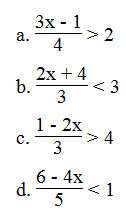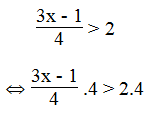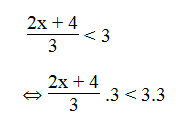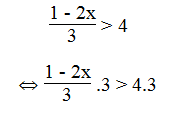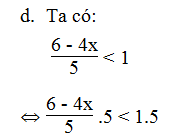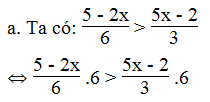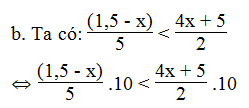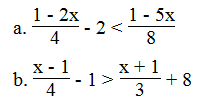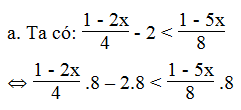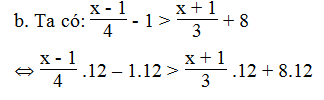Giải SBT Toán 8 trang 56, 57, 58 tập 2 Bài 4 chi tiết nhất

Lời giải Sách bài tập Toán lớp 8 tập 2 trang 56, 57, 58 tập 2 Bài 4: Bất phương trình bậc nhất một ẩn gồm các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải bài 40 SBT Toán lớp 8 tập 2 trang 56

Áp dụng quy tắc chuyển vế để giải các bất phương trình sau:

a. x – 2 > 4

b. x + 5 < 7

c. x – 4 < -8

d. x + 3 > - 6

Lời giải:

a. Ta có: x – 2 > 4 ⇔ x > 4 + 2 ⇔ x > 6

Vậy tập nghiệm của bất phương trình là: {x|x > 6}

b. Ta có: x + 5 < 7 ⇔ x < 7 – 5 ⇔ x < 2

Vậy tập nghiệm của bất phương trình là: {x|x < 2}

c. Ta có: x – 4 < -8 ⇔ x < -8 + 4 ⇔ x < -4

Vậy tập nghiệm của bất phương trình là: {x|x < -4}

d. Ta có: x + 3 > -6 ⇔ x > -6 – 3 ⇔ x > -9

Vậy tập nghiệm của bất phương trình là: {x|x > -9}

Giải bài 41 trang 56 SBT lớp 8 Toán tập 2

Áp dụng quy tắc chuyển vế, giải các bất phương trình sau:

a. 3x < 2x + 5

b. 2x + 1 < x + 4

c. -2x > -3x + 3

d. -4x – 2 > -5x + 6

Lời giải:

a. Ta có: 3x < 2x + 5 ⇔ 3x – 2x < 5 ⇔ x < 5

Vậy tập nghiệm của bất phương trình là: {x|x < 5}

b. Ta có: 2x + 1 < x + 4 ⇔ 2x – x < 4 – 1 ⇔ x < 3

Vậy tập nghiệm của bất phương trình là: {x|x < 3}

c. Ta có: -2x > -3x + 3 ⇔ -2x + 3x > 3 ⇔ x > 3

Vậy tập nghiệm của bất phương trình là: {x|x > 3}

d. Ta có: -4x – 2 > -5x + 6 ⇔ -4x + 5x > 6 + 2 ⇔ x > 8

Vậy tập nghiệm của bất phương trình là: {x|x > 8}

Giải bài 42 Toán lớp 8 SBT trang 56 tập 2

Áp dụng quy tắc nhân để giải các bất phương trình sau:

Lời giải:

a. Ta có: 1/2 x > 3 ⇔ 1/2 x.2 > 3.2 ⇔ x > 6

Vậy tập nghiệm của bất phương trình là: {x|x > 6}

b. Ta có: -1/3 x < -2 ⇔ -1/3 x.(-3) > (-2).(-3) ⇔ x > 6

Vậy tập nghiệm của bất phương trình là: {x|x > 6}

c. Ta có: 2/3 x > -4 ⇔ 2/3 x. 3/2 > -4. 3/2 ⇔ x > -6

Vậy tập nghiệm của bất phương trình là: {x|x > -6}

d. Ta có: -3/5 x > 6 ⇔ -3/5 x.(-5/3 ) < 6.(-5/3 ) ⇔ x < -10

Vậy tập nghiệm của bất phương trình là: {x|x < -10}

Giải bài 43 trang 56 tập 2 SBT Toán lớp 8

Áp dụng quy tắc nhân, giải các bất phương trình sau:

a. 3x < 18

b. -2x > -6

c. 0,2x > 8

d. -0,3x < 12

Lời giải:

a. Ta có: 3x < 18

Vậy tập nghiệm của bất phương trình là: {x|x < 6}

b. Ta có: -2x > -6

Vậy tập nghiệm của bất phương trình là: {x|x < 3}

c. Ta có: 0,2x > 8 ⇔ 0,2x.5 > 8.5 ⇔ x > 40

Vậy tập nghiệm của bất phương trình là: {x|x > 40}

d. Ta có: -0,3x < 12

Vậy tập nghiệm của bất phương trình là: {x|x > -40}

Giải bài 44 SBT Toán trang 56 tập 2 lớp 8

Giải thích sự tương đương:

a. 2x < 3 ⇔ 3x < 4,5

b. x – 5 < 12 ⇔ x + 5 < 22

c. -3x < 9 ⇔ 6x > -18

Lời giải:

a. Nhân hai vế của bất phương trình 2x < 3 với 1,5.

b. Cộng hai vế của bất phương trình x – 5 < 12 với 10.

c. Nhân hai vế của bất phương trình -3x < 9 với -2.

Giải bài 45 Toán SBT lớp 8 trang 56 tập 2

Cho hình vẽ:

Bạn An cho rằng, hình vẽ đó biểu diễn tập nghiệm của bất phương trình 2x ≤ 16, còn bạn Bình lại khẳng định hình vẽ đó biểu diễn tập nghiệm của bất phương trình x + 2 ≤ 10. Theo em bạn nào đúng?

Lời giải:

Ta có: 2x ≤ 16 ⇔ x ≤ 8

x + 2 ≤ 10 ⇔ x ≤ 8

Như vậy cả hai bạn đều phát biểu đúng.

Giải bài 46 lớp 8 SBT Toán tập 2 trang 57

Giải các bất phương trình và biểu diễn tập nghiệm trên trục số

a. 2x – 4 < 0

b. 3x + 9 > 0

c. –x + 3 < 0

d. -3x + 12 > 0

Lời giải:

a. Ta có: 2x – 4 < 0 ⇔ 2x < 4 ⇔ x < 2

b. Ta có: 3x + 9 > 0 ⇔ 3x > -9 ⇔ x > -3

c. Ta có: -x + 3 < 0 ⇔ -x < -3 ⇔ x > 3

d. Ta có: -3x + 12 > 0 ⇔ -3x > -12 ⇔ x < 4

Giải bài 47 trang 57 Toán tập 2 lớp 8 SBT

Giải các bất phương trình:

a. 3x + 2 > 8

b. 4x – 5 < 7

c. -2x + 1 < 7

d. 13 – 3x > -2

Lời giải:

a. Ta có: 3x + 2 > 8 ⇔ 3x > 8 – 2 ⇔ 3x > 6 ⇔ x > 2

Vậy tập nghiệm của bất phương trình là: {x|x > 2}

b. Ta có: 4x – 5 < 7 ⇔ 4x < 7 + 5 ⇔ 4x < 12 ⇔ x < 3

Vậy tập nghiệm của bất phương trình là: {x|x < 3}

c. Ta có: -2x + 1 < 7 ⇔ -2x < 7 – 1 ⇔ -2x < 6 ⇔ x > -3

Vậy tập nghiệm của bất phương trình là: {x|x > -3}

d. Ta có: 13 – 3x > -2 ⇔ -3x > -2 – 13 ⇔ -3x > -15 ⇔ x < 5

Vậy tập nghiệm của bất phương trình là: {x|x < 5}

Giải bài 48 SBT Toán tập 2 lớp 8 trang 57

Giải các bất phương trình:

a. 3/2 x < -9

b. 5 + 2/3 x > 3

c. 2x + 4/5 > 9/5

d. 6 - 3/5 x < 4

Lời giải:

a. Ta có:

Vậy tập nghiệm của bất phương trình là: {x|x < -6}

b. Ta có: 5 + 2/3 x > 3 ⇔ 2/3 x > 3 – 5 ⇔ 2/3 x. 3/2 > -2. 3/2 ⇔ x > -3

Vậy tập nghiệm của bất phương trình là: {x|x > -3}

c. Ta có:

Vậy tập nghiệm của bất phương trình là: {x|x > 1/2 }

d. Ta có: 6 - 3/5 x < 4 ⇔ -3/5 x < 4 – 6 ⇔ -3/5 x.(-5/3 ) > -2.(-5/3 ) ⇔ x > 10/3

Vậy tập nghiệm của bất phương trình là: {x|x > 10/3 }

Giải bài 49 SBT Toán lớp 8 tập 2 trang 57

Giải các bất phương trình:

a. 7x – 2,2 < 0,6

b. 1,5 > 2,3 – 4x

Lời giải:

a. Ta có: 7x – 2,2 < 0,6

⇔ 7x < 0,6 + 2,2

⇔ 7x < 2,8

⇔ x < 0,4

Vậy tập nghiệm của bất phương trình là: {x|x < 0,4}

b. Ta có: 1,5 > 2,3 – 4x

⇔ 4x > 2,3 - 1,5

⇔ 4x > 0,8

⇔ x > 0,2

Vậy tập nghiệm của bất phương trình là: {x|x > 0,2}

Giải bài 50 trang 57 SBT lớp 8 Toán tập 2

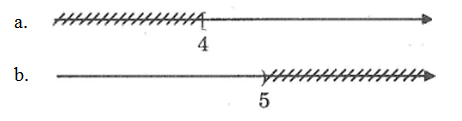
Viết bất phương trình bậc nhất một ẩn có tập nghiệm biểu diễn bởi hình vẽ.

Lời giải:

a. Bất phương trình bậc nhất một ẩn có tập nghiệm biểu diễn bởi hình vẽ là:

2x – 8 ≥ 0

b. Bất phương trình bậc nhất một ẩn có tập nghiệm biểu diễn bởi hình vẽ là:

3x – 15 < 0

Giải bài 51 Toán lớp 8 SBT trang 57 tập 2

Giải các bất phương trình:

Lời giải:

a. Ta có:

⇔ 3x – 1 > 8

⇔ 3x > 8 + 1

⇔ 3x > 9 ⇔ x > 3

Vậy tập nghiệm của bất phương trình là: {x|x > 3}

b. Ta có:

⇔ 2x + 4 < 9

⇔ 2x < 9 – 4

⇔ 2x < 5 ⇔ x < 2,5

Vậy tập nghiệm của bất phương trình là: {x|x < 2,5}

c. Ta có:

⇔ 1 – 2x > 12

⇔ -2x > 12 – 1

⇔ -2x > 11 ⇔ x < -5,5

Vậy tập nghiệm của bất phương trình là: {x|x < -5,5}

d. Ta có:

⇔ 6 – 4x < 5

⇔ -4x < 5 – 6

⇔ -4x < -1 ⇔ x > 1/4

Vậy tập nghiệm của bất phương trình là: {x|x > 1/4 }

Giải bài 52 trang 57 tập 2 SBT Toán lớp 8

Giải các bất phương trình:

a. (x – 1)² < x(x + 3)

b. (x – 2)(x + 2) > x(x – 4)

c. 2x + 3 < 6 – (3 – 4x)

d. -2 – 7x > (3 + 2x) – (5 – 6x)

Lời giải:

a. Ta có: (x – 1)² < x(x + 3) ⇔ x² – 2x + 1 < x² + 3x

⇔ x² – 2x + 1 – x² – 3x < 0

⇔ -5x + 1 < 0 ⇔ 5x > 1 ⇔ x > 1/5.

Vậy tập nghiệm của bất phương trình là: {x| x > 1/5}

b. Ta có: (x – 2)(x + 2) > x(x – 4) ⇔ x² – 4 > x² – 4x

⇔ x² – 4 – x² + 4x > 0

⇔ 4x – 4 > 0 ⇔ x > 1

Vậy tập nghiệm của bất phương trình là: {x|x > 1}

c. Ta có: 2x + 3 < 6 – (3 – 4x) ⇔ 2x + 3 < 6 – 3 + 4x

⇔ 2x – 4x < 3 – 3

⇔ -2x < 0 ⇔ x > 0

Vậy tập nghiệm của bất phương trình là: {x|x > 0}

d. Ta có: -2 – 7x > (3 + 2x) – (5 – 6x) ⇔ -2 – 7x > 3 + 2x – 5 + 6x

⇔ -7x – 2x – 6x > 3 – 5 + 2

⇔ -15x > 0 ⇔ x < 0

Vậy tập nghiệm của bất phương trình là: {x|x < 0}

Giải bài 53 SBT Toán trang 57 tập 2 lớp 8

Với các giá trị nào của x thì:

a. Giá trị phân thức (5 - 2x)/6 lớn hơn giá trị phân thức (5x - 2)/3

b. Giá trị phân thức (1,5 - x)/5 nhỏ hơn giá trị phân thức (4x + 5)/2

Lời giải:

⇔ 5 – 2x > 10x – 4

⇔ -2x – 10x > -4 – 5⇔ -12x > -9⇔ x < 3/4

Vậy với x < 3/4 thì giá trị phân thức (5 - 2x)/6 lớn hơn giá trị phân thức (5x - 2)/3

⇔ 3 – 2x < 20x + 25⇔ -2x – 20x < 25 – 3

⇔ -22x < 22⇔ x > -1

Vậy với x > -1 thì giá trị phân thức (1,5 - x)/5 nhỏ hơn giá trị phân thức 4x + 5)/2 .

Giải bài 54 Toán SBT lớp 8 trang 58 tập 2

Hãy cho biết số nào trong các số 2/3 ; 2/7 ; -4/5 là nghiệm của bất phương trình 5 – 3x < (4 + 2x) – 1

Lời giải:

Ta có: 5 – 3x < (4 + 2x) – 1 ⇔ 5 – 3x < 4 + 2x – 1

⇔ -3x – 2x < 4 – 1 – 5 ⇔ -5x < -2 ⇔ x > 2/5

Vậy chỉ có giá trị 2/3 > 2/5 nên trong các số đã cho thì số 2/3 là nghiệm của bất phương trình.

Giải bài 55 lớp 8 SBT Toán tập 2 trang 58

Hai quy tắc biến đổi tương đương của bất phương trình cũng giống như hai quy tắc biến đổi tương đương của phương trình. Điều đó có đúng không?

Lời giải:

Ta có, quy tắc chuyển vế của phương trình giống quy tắc chuyển vế của bất phương trình, nhưng quy tắc nhân hai vế của phương trình với cùng một số khác 0 không thể chuyển thành quy tắc nhân hai vế của bất phương trình với cùng một số khác 0, bởi vì bất phường trình sẽ đổi chiều khi ta nhân hai vế của nó với một số âm.

Giải bài 56 trang 58 Toán tập 2 lớp 8 SBT

Cho bất phương trình ẩn x: 2x + 1 > 2(x + 1).

a. Chứng tỏ các giá trị -5; 0; -8 đều không phải là nghiệm của nó.

b. Bất phương trình này có thể nhận giá trị nào của x là nghiệm?

Lời giải:

a. Thay giá trị của x vào từng vế của bất phương trình:

x = -5 vế trái: 2.(-5) + 1 = -10 + 1 = -9

vế phải: 2.[(-5) + 1] = 2.(-4) = -8

Vì -9 < -8 nên x = -5 không phải là nghiệm của bất phương trình.

x = 0 vế trái: 2.0 + 1 = 1

vế phải: 2.(0 + 1) = 2

Vì 1 < 2 nên x = 0 không phải là nghiệm của bất phương trình.

x = -8 vế trái: 2.(-8) + 1 = -16 + 1 = -15

vế phải: 2.[(-8) + 1] = 2.(-7) = -14

Vì -15 < -14 nên x = -8 không là nghiệm của bất phương trình.

b. Ta có: 2x + 1 > 2(x + 1)

      ⇔ 2x + 1 > 2x + 2

      ⇔ 0x > 1

Vậy bất phương trình vô nghiệm.

Giải bài 57 SBT Toán tập 2 lớp 8 trang 58

Bất phương trình ẩn x: 5 + 5x < 5(x + 2). Có thể nhận giá trị nào của x là nghiệm?

Lời giải:

Ta có: 5 + 5x < 5(x + 2)

⇔ 5 + 5x < 5x + 10

⇔ 5x – 5x < 10 – 5

⇔ 0x < 5

Bất kì giá trị nào của x cũng thỏa mãn vế trái nhỏ hơn vế phải.

Vậy tập nghiệm của bất phương trình là tập số thực R.

Giải bài 58 SBT Toán lớp 8 tập 2 trang 58

So sánh số a và số b nếu:

a. x < 5 ⇔ (a – b)x < 5(a – b)

b. x > 2 ⇔ (a – b)x < 2(a – b)

Lời giải:

a. Ta có: x < 5 ⇔ (a – b)x < 5(a – b)

⇒ a – b > 0 ⇔ a > b

b. Ta có: x > 2 ⇔ (a – b)x < 2(a – b)

⇒ a – b < 0 ⇔ a < b

Giải bài 59 trang 58 SBT lớp 8 Toán tập 2

Tìm số nguyên x lớn nhất thỏa mãn mỗi bất phương trình sau:

a. 5,2 + 0,3x < - 0,5

b. 1,2 – (2,1 – 0,2x) < 4,4

Lời giải:

a. Ta có: 5,2 + 0,3x < - 0,5

⇔ 0,3x < - 0,5 – 5,2

⇔ 0,3x < - 5,7

⇔ x < -19

Vậy số nguyên lớn nhất cần tìm là -20

b. Ta có: 1,2 – (2,1 – 0,2x) < 4,4

⇔ 1,2 -2,1 + 0,2x < 4,4

⇔ 0,2x < 4,4 – 1,2 + 2,1

⇔ 0,2x < 5,3

⇔ x < 53/2

Vậy số nguyên lớn nhất thỏa mãn điều kiện là số 26.

Giải bài 60 Toán lớp 8 SBT trang 58 tập 2

Tìm số nguyên x bé nhất thỏa mãn mỗi bất phương trình sau:

a. 0,2x + 3,2 > 1,5

b. 4,2 – (3 – 0,4x) > 0,1x + 0,5

Lời giải:

a. Ta có: 0,2x + 3,2 > 1,5

       ⇔ 0,2x > 1,5 – 3,2

       ⇔ 0,2x > - 1,7

       ⇔ x > - 17/2

Vậy số nguyên bé nhất cần tìm là – 8.

b. Ta có: 4,2 – (3 – 0,4x) > 0,1x + 0,5

       ⇔ 4,2 – 3 + 0,4x > 0,1x + 0,5

       ⇔ 0,4x – 0,1x > 0,5 – 1,2

       ⇔ 0,3x > - 0,7

       ⇔ x > - 7/3

Vậy số nguyên bé nhất cần tìm là -2.

Giải bài 61 trang 58 tập 2 SBT Toán lớp 8

Với giá trị nào của m thì phương trình ẩn x:

a. x – 3 = 2m + 4 có nghiệm dương?

b. 2x – 5 = m + 8 có nghiệm số âm?

Lời giải:

a. Ta có x – 3 = 2m + 4

      ⇔ x = 2m + 4 + 3

      ⇔ x = 2m + 7

Phương trình có nghiệm số dương khi 2m + 7 > 0 ⇔ m > - 7/2

b. Ta có: 2x – 5 = m + 8

      ⇔ 2x = m + 8 + 5

      ⇔ 2x = m + 13

      ⇔ x = (m + 13)/2

Phương trình có nghiệm số âm khi (m + 13)/2 < 0 ⇔ m + 13 < 0 ⇔ m < -13

Giải bài 62 SBT Toán trang 58 tập 2 lớp 8

Giải các bất phương trình:

a. (x + 2)² < 2x(x + 2) + 4

b. (x + 2)(x + 4) > (x – 2)(x + 8) + 26

Lời giải:

a. Ta có: (x + 2)² < 2x(x + 2) + 4

      ⇔ x² + 4x + 4 < 2x² + 4x + 4

      ⇔ x² + 4x – 2x² – 4x < 4 – 4

      ⇔ -x² < 0

      ⇔ x² > 0

Vậy tập nghiệm của bất phương trình là: {x|x ≠ 0}

b. Ta có: (x + 2)(x + 4) > (x – 2)(x + 8) + 26

      ⇔ x² + 6x + 8 > x² + 6x + 10

      ⇔ x² + 6x - x² - 6x > 10 - 8

       ⇔ 0x > 2

Vậy bất phương trình vô nghiệm.

Giải bài 63 Toán SBT lớp 8 trang 58 tập 2

Giải các bất phương trình:

Lời giải:

⇔ 2 – 4x – 16 < 1 – 5x

⇔ -4x + 5x < 1 – 2 + 16

⇔ x < 15

Vậy tập nghiệm của bất phương trình là: {x|x < 15}

⇔ 3x – 3 – 12 > 4x + 4 + 96

⇔ 3x – 4x > 4 + 96 + 3 + 12

⇔ -x > 115 ⇔ x < -115

Vậy tập nghiệm của bất phương trình là: {x|x < -115}

Giải bài 64 lớp 8 SBT Toán tập 2 trang 58

Tìm các số tự nhiên n thỏa mãn mỗi bất phương trình sau:

a. 3(5 – 4n) + (27 + 2n) > 0

b. (n + 2)² – (n – 3)(n + 3) ≤ 40

Lời giải:

a. Ta có: 3(5 – 4n) + (27 + 2n) > 0

      ⇔ 15 – 12n + 27 + 2n > 0

      ⇔ -10n + 42 > 0

      ⇔ -10n > -42

      ⇔ n < 4,2

Vậy các số tự nhiên cần tìm là 0; 1; 2; 3; 4.

b. Ta có: (n + 2)² – (n – 3)(n + 3) ≤ 40

       ⇔ n² + 4n + 4 – n² + 9 ≤ 40

       ⇔ 4n < 40 – 13

       ⇔ n < 27/4

Vậy các số tự nhiên cần tìm là 0; 1; 2; 3; 4; 5; 6.

►► CLICK NGAY vào TẢI VỀ dưới đây để download hướng dẫn giải Sách bài tập Toán lớp 8 tập 2 trang 56, 57, 58 file word, pdf hoàn toàn miễn phí.