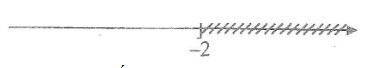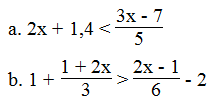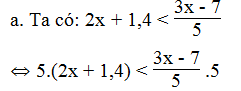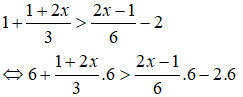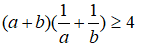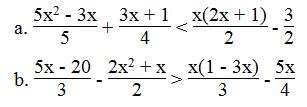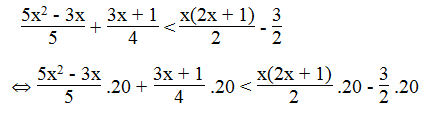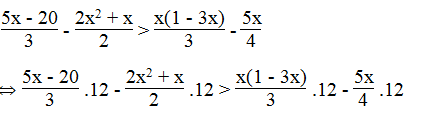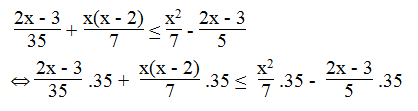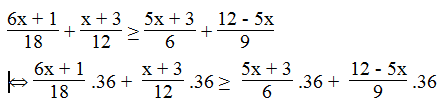Giải SBT Toán 8 trang 61, 62 tập 2 Bài 5 Bài: Ôn tập chương 4 - Phần Đại số

Lời giải Sách bài tập Toán lớp 8 trang trang 61, 62 tập 2 Bài: Ôn tập chương 4 - Phần Đại số gồm các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải bài 71 SBT Toán lớp 8 tập 2 trang 61

Cho các bất đẳng thức:

a > b; a < b; c > 0; c < 0; a + c < b + c; a + c > b + c; ac < bc; ac > bc

Hãy điển các bất đẳng thức thích hợp vào chỗ trống (...) trong câu sau: Nếu……… và………. thì………..

Lời giải:

Nếu a > b và c > 0 thì ac > bc

Nếu a > b và c > 0 thì a + c > b + c

Nếu a > b và c < 0 thì a + c > b + c

Nếu a > b và c < 0 thì ac < bc

Nểu a < b và c > 0 thì ac < bc

Nếu a < b và c > 0 thì a + c < b + c

Nếu a < b và c < 0 thì ac > bc

Nếu a < b và c < 0 thì a + c < b + c

Giải bài 72 trang 61 SBT lớp 8 Toán tập 2

Cho a > b, chứng tỏ:

a. 3a + 5 > 3b + 2

b. 2 – 4a < 3 – 4b

Lời giải:

a. Ta có: a > b ⇔ 3a > 3b ⇔ 3a + 5 > 3b + 5 (1)

Mặt khác: 3b + 5 > 3b + 2 (2)

Từ (1) và (2) suy ra: 3a + 5 > 3b + 2

b. Ta có: a > b ⇔ -4a < -4b ⇔ 3 – 4a < 3 – 4b (1)

Mặt khác: 2 – 4a < 3 – 4a (2)

Từ (1) và (2) suy ra: 2 – 4a < 3 – 4b

Giải bài 73 Toán lớp 8 SBT trang 61 tập 2

a. Chứng tỏ 2,99 là nghiệm của bất phương trình 3 > x. Hãy kể ra bốn số lớn hơn 2,99 là nghiệm của bất phương trình đó.

b. Chứng tỏ 4,01 là nghiệm của bất phương trình 4 < x. Hãy kể ra ba số nhỏ hơn 4,01 là nghiệm của bất phương trình đó.

Lời giải:

a. Ta có 2,99 là nghiệm của bất phương trình x < 3. Bốn số lớn hơn 2,99 là nghiệm của bất phương trình là: 2,999; 2,998; 2,997; 2,996.

b. Ta có 4,01 là nghiệm của bất phương trình x > 4. Ba số nhỏ hơn 4,01 là nghiệm của bất phương trình là: 4,003; 4,002; 4,001.

Giải bài 74 trang 61 tập 2 SBT Toán lớp 8

Giải các bất phương trình và biểu diễn tập nghiệm của chúng trên trục số.

a. 2(3x – 1) – 2x < 2x + 1

b. 4x – 8 ≥ 3(3x – 2) + 4 – 2x

Lời giải:

a. Ta có: 2(3x – 1) – 2x < 2x + 1

      ⇔ 6x – 2 – 2x < 2x – 1

       ⇔ 6x – 2x – 2x < -1 + 2

       ⇔ 2x < 1

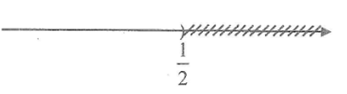
       ⇔ x < 1/2

Vậy tập nghiệm của bất phương trình là {x|x < 1/2 }

b. Ta có: 4x – 8 ≥ 3(3x – 2) + 4 – 2x

       ⇔ 4x – 8 ≥ 9x – 6 + 4 – 2x

       ⇔ 4x – 9x + 2x ≥ - 6 + 4 + 8

      ⇔ -3x ≥ 6

      ⇔ x ≤ -2

Vậy tập nghiệm của bất phương trình là {x|x ≤ -2}

Giải bài 75 SBT Toán trang 61 tập 2 lớp 8

Giải các bất phương trình:

Lời giải:

      ⇔ 10x + 7 < 3x – 7

      ⇔ 10x – 3x < -7 – 7

      ⇔ 7x < -14

      ⇔ x < -2

Vậy tập nghiệm của bất phương trình là {x|x < -2}

b. Ta có:

      ⇔ 6 + 2 + 4x > 2x – 1 – 12

      ⇔ 4x – 2x > -1 – 12 – 6 – 2

      ⇔ 2x > -21

      ⇔ x > -10,5

Vậy tập nghiệm của bất phương trình là {x|x > -10,5}

Giải bài 76 Toán SBT lớp 8 trang 61 tập 2

Một người đi bộ quãng đường dài 18km trong khoảng thời gian không nhiều hơn 4 giờ. Lúc đầu người đó đi với vận tốc 5km/h, về sau đi với vận tốc 4km/h. Xác định độ dài đoạn đường mà người đó đã đi với vận tốc 5km/h.

Lời giải:

Gọi x (km) là đoạn đường người đó đi với vận tốc 5km/h. ĐK: x < 18.

Khi đó đoạn đường người đó đi với vận tốc 4km/h là 18 – x(km)

Thời gian đi với vận tốc 5km/h là x/5 giờ

Thời gian đi với vận tốc 4km/h là (18 - x)/4 giờ.

Vì thời gian đi hết đoạn đường không quá 4 giờ nên ta có bất phương trình: x/5 + (18 - x)/4 ≤ 4.

Ta có: x/5 + (18 - x)/4 ≤ 4

      ⇔ x/5 .20 + (18 - x)/4 .20 ≤ 4.20

      ⇔ 4x + 90 – 5x ≤ 80

      ⇔ 4x – 5x ≤ 80 – 90

      ⇔ -x ≤ -10

      ⇔ x ≥ 10

Vậy đoạn đường đi với vận tốc 5km/h ít nhất là 10km.

Giải bài 77 lớp 8 SBT Toán tập 2 trang 61

Giải các phương trình:

a. |2x| = 3x – 2

b. |-3,5x| = 1,5x + 5

c. |x + 15| = 3x – 1

d. |2 – x| = 0,5x – 4

Lời giải:

a. Ta có: |2x| = 2x khi 2x ≥ 0 ⇔ x ≥ 0

       |2x| = -2x khi 2x < 0 ⇔ x < 0

Ta có: 2x = 3x – 2

      ⇔ 2x – 3x = -2

       ⇔ x = 2

Giá trị x = 2 thỏa mãn điều kiện x ≥ 0 nên 2 là nghiệm của phương trình.

       -2x = 3x – 2

       ⇔ -2x – 3x = -2

       ⇔ x = 2/5

Giá trị x = 2/5 không thỏa mãn điều kiện x < 0 nên loại.

Vậy tập nghiệm của phương trình là S = {2}

b. Ta có: |-3,5x| = -3,5x khi -3,5x ≥ 0 ⇔ x ≤ 0

       |-3,5x| = 3,5x khi -3,5x < 0 ⇔ x > 0

Ta có: -3,5x = 1,5x + 5

      ⇔ -3,5x – 1,5x = 5

      ⇔ -5x = 5

      ⇔ x = -1

Giá trị x = -1 thỏa mãn điều kiện x ≤ 0 nên -1 là nghiệm của phương trình.

       3,5x = 1,5x + 5

       ⇔ 3,5x – 1,5x = 5

       ⇔ 2x = 5

       ⇔ x = 2,5

Giá trị x = 2,5 thỏa mãn điều kiện x > 0 nên 2,5 là nghiệm của phương trình.

Vậy tập nghiệm của phương trình là S = {-1; 2,5}

c. Ta có: |x + 15| = x + 15 khi x + 15 ≥ 0 ⇔ x ≥ -15

       |x + 15| = -x – 15 khi x + 15 < 0 ⇔ x < -15

Ta có: x + 15 = 3x – 1

      ⇔ x – 3x = -1 – 15

      ⇔ -2x = -16

      ⇔ x = 8

Giá trị x = 8 thỏa mãn điều kiện x ≥ -15 nên 8 là nghiệm của phương trình.

       -x – 15 = 3x – 1

       ⇔ -x – 3x = -1 + 15

       ⇔ -4x = 14

       ⇔ x = -3,5

Giá trị x = -3,5 không thỏa mãn điều kiện x < -15 nên loại.

Vậy tập nghiệm của phương trình là S = {8}

d. Ta có: |2 – x| = 2 – x khi 2 – x ≥ 0 ⇔ x ≤ 2

       |2 – x| = x – 2 khi 2 – x < 0 ⇔ x > 2

Ta có: 2 – x = 0,5x – 4

      ⇔ -x – 0,5x = -4 + 2

      ⇔ 0,5x = -2

      ⇔ x = -4

Giá trị x = -4 thỏa mãn điều kiện x ≤ 2 nên loại.

       x – 2 = 0,5x – 4

       ⇔ -x – 0,5x = -4 - 2

       ⇔ -1,5x = -2

       ⇔ x = 4

Giá trị x = -4 không thỏa mãn điều kiện x > 2 nên loại.

Vậy tập nghiệm của phương trình là S = ∅.

Giải bài 78 trang 61 Toán tập 2 lớp 8 SBT

Chứng tỏ rằng, trong một tam giác độ dài một cạnh luôn nhỏ hơn nửa chu vi.

Lời giải:

Gọi a, b, c lần lượt là độ dài ba cạnh của tam giác.

Chu vi tam giác là a + b + c.

Theo bất đẳng thức tam giác, ta có:

      a < b + c

      ⇔ a + a < a + b + c

      ⇔ 2a < a + b + c

      ⇔ a < (a + b + c)/2

Tương tự:

      b < a + c

      ⇔ b + b < a + b + c

      ⇔ 2b < a + b + c

      ⇔ b < (a + b + c)/2

      c < a + b

      ⇔ c + c < a + b + c

      ⇔ 2c < a + b + c

      ⇔ c < (a + b + c)/2

Vậy trong một tam giác độ dài một cạnh luôn nhỏ hơn nửa chu vi.

Giải bài 79 SBT Toán tập 2 lớp 8 trang 61

Với số m và số n bất kì, chứng tỏ rằng:

a. (m + 1)² ≥ 4m

b. m² + n² + 2 ≥ 2(m + n)

Lời giải:

a. Ta có: (m – 1)² ≥ 0

       ⇔ (m – 1)² + 4m ≥ 4m

      ⇔ m² – 2m + 1 + 4m ≥ 4m

       ⇔ m² + 2m + 1 ≥ 4m

      ⇔ (m + 1)² ≥ 4m

b. Ta có: (m – 1)² ≥ 0; (n – 1)² ≥ 0

       ⇒ (m – 1)² + (n – 1)² ≥ 0

       ⇔ m² – 2m + 1 + n² – 2n + 1 ≥ 0

       ⇔ m² + n² + 2 ≥ 2(m + n)

Giải bài 80 Toán SBT tập 2 lớp 8 trang 61

Cho a > 0 và b > 0, chứng tỏ rằng: 

Lời giải:

Ta có: (a – b)² ≥ 0

      ⇔ a² + b² – 2ab ≥ 0

      ⇔ a² + b² – 2ab + 2ab ≥ 2ab

      ⇔ a² + b² ≥ 2ab

Vì a ≥ 0, b ≥ 0 nên ab ≥ 0 ⇒ 1/ab ≥ 0

       (a² + b²).1/ab ≥ 2ab.1/ab

       ⇔ a/b + b/a ≥ 2

       ⇔ 2 + a/b + b/a ≥ 2 + 2

       ⇔ 2 + a/b + b/a ≥ 4

       ⇔ 1 + 1 + a/b + b/a ≥ 4

      ⇔ a/a + b/b + a/b + b/a ≥ 4

      ⇔ a(1/a + 1/b ) + b(1/a + 1/b ) ≥ 4

      ⇔ (a + b)(1/a + 1/b ) ≥ 4

Giải bài 81 SBT Toán lớp 8 tập 2 trang 62

Chứng tỏ diện tích của hình vuông có cạnh 10m không nhỏ hơn diện tích hình chữ nhật có cùng chu vi.

Lời giải:

Chu vi hình vuông là 4.10 = 40 (m)

Suy ra, chu vi hình chữ nhật là 40(m)

Gọi x (m) là chiều rộng hình chữ nhật. Điều kiện: x < 20.

Khi đó chiều dài hình chữ nhật là 20 – x (m).

Diện tích hình chữ nhật là x(20 – x) (m²).

Vậy ta cần chứng minh: 10² ≥ x(20 – x)

Ta có: (10 – x)² ≥ 0

       ⇔ 10² – 20x + x² ≥ 0

       ⇔ 10² ≥ 20x – x²

       ⇔ 10² ≥ x(20 – x)

Vậy diện tích hình vuông cạnh 10m không nhỏ hơn diện tích hình chữ nhật cùng chu vi.

Giải bài 82 trang 62 SBT lớp 8 Toán tập 2

Giải các bất phương trình:

a. 3(x – 2)(x + 2) < 3x² + x

b. (x + 4)(5x – 1) > 5x² + 16x + 2

Lời giải:

a. Ta có: 3(x – 2)(x + 2) < 3x² + x

       ⇔ 3(x² – 4) < 3x² + x

       ⇔ 3x² – 12 < 3x² + x

       ⇔ 3x² – 3x² – x < 12

       ⇔ -x < 12

       ⇔ x > -12

Vậy tập nghiệm của bất phương trình là S = {x|x > -12}

b. Ta có: (x + 4)(5x – 1) > 5x² + 16x + 2

       ⇔ 5x² – x + 20x – 4 > 5x² + 16x + 2

       ⇔ 5x² – x + 20x – 5x² – 16x > 2 + 4

       ⇔ 3x > 6

       ⇔ x > 2

Vậy tập nghiệm của bất phương trình là S = {x|x > 2}

Giải bài 83 Toán lớp 8 SBT trang 62 tập 2

Giải các bất phương trình:

Lời giải:

a. Ta có:

      ⇔ 20x² – 12x + 15x + 5 < 20x² + 10x – 30

      ⇔ 20x² – 12x + 15x – 20x² – 10x < -30 – 5

      ⇔ -7x < -35

      ⇔ x > 5

Vậy tập nghiệm của bất phương trình là {x|x > 5}

b. Ta có:

      ⇔ 20x – 80 – 12x² – 6x > 4x – 12x² – 15x

      ⇔ 20x – 12x² – 6x – 4x + 12x² + 15x > 80

      ⇔ 25x > 80

      ⇔ x > 3,2

Vậy tập nghiệm của bất phương trình là {x|x > 3,2}

Giải bài 84 trang 62 tập 2 SBT Toán lớp 8

Với giá trị nào của x thì:

a. Giá trị của biểu thức 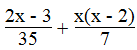 không lớn hơn giá trị của biểu thức 

b. Giá trị của biểu thức  không nhỏ hơn giá trị của biểu thức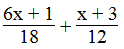

Lời giải:

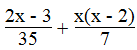
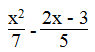
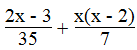
a. Giá trị của biểu thức  không lớn hơn giá trị của biểu thức  nghĩa là  ≤ 

Ta có:

      ⇔ 2x – 3 + 5x² – 10x ≤ 5x² – 14x + 21

      ⇔ 2x + 5x² – 10x – 5x² + 14x ≤ 21 + 3

      ⇔ 6x ≤ 24

      ⇔ x ≤ 4

Vậy với x ≤ 4 thì giá trị của biểu thức 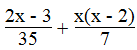 không lớn hơn giá trị của biểu thức 

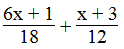
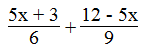
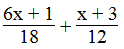
b. Giá trị của biểu thức  không nhỏ hơn giá trị của biểu thức nghĩa là  ≥ 

Ta có:

      ⇔ 12x + 2 + 3x + 9 ≥ 30x + 18 + 48 – 20x

      ⇔ 12x + 3x – 30x + 20x ≥ 18 + 48 – 2 – 9

      ⇔ 5x ≥ 55

      ⇔ x ≥ 11

Vậy với x ≥ 11 thì giá trị của biểu thức  không nhỏ hơn giá trị của biểu thức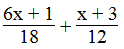

Giải bài 85 SBT Toán trang 62 tập 2 lớp 8

Tìm x sao cho:

a. –x² < 0

b. (x – 1)x < 0

Lời giải:

a. Ta có: -x² < 0 ⇔ x² > 0

Mọi giá trị x ≠ 0 đều là nghiệm của bất phương trình.

Tập hợp các giá trị của x là {x ∈ R|x ≠ 0}

b. Trường hợp 1: x – 1 > 0 và x < 0

Ta có: x – 1 > 0 ⇔ x > 1 và x < 0

Điều này không xảy ra: loại.

Trường hợp 2: x – 1 < 0 và x > 0

Ta có: x – 1 < 0 ⇔ x < 1 và x > 0

Suy ra: 0 < x < 1

Vậy tập hợp các giá trị của x là {x|0 < x < 1}

Giải bài 86 Toán SBT lớp 8 trang 62 tập 2

Tìm x sao cho:

a. x² > 0

b. (x – 2)(x – 5) > 0

Lời giải:

a. Với x² > 0 thì mọi x khác 0 đều thỏa mãn bài toán.

Tập hợp các giá trị của x là {x ∈ R|x ≠ 0}

b. Trường hợp 1: x – 2 > 0 và x – 5 > 0

Ta có: x – 2 > 0 ⇔ x > 2

x – 5 > 0 ⇔ x > 5

Suy ra: x > 5

Trường hợp 2: x – 2 < 0 và x – 5 < 0

Ta có: x – 2 < 0 ⇔ x < 2

x – 5 < 0 ⇔ x < 5

Suy ra: x < 2

Vậy với x > 5 hoặc x < 2 thì (x – 2)(x – 5) > 0.

Giải bài 87 lớp 8 SBT Toán tập 2 trang 62

Với giá trị nào của x thì:

a. (x - 2)/(x - 3) > 0

b. (x + 2)/(x - 5) < 0

Lời giải:

a. Trường hợp 1: x – 2 > 0 và x – 3 > 0

Ta có: x – 2 > 0 ⇔ x > 2

x – 3 > 0 ⇔ x > 3

Suy ra: x > 3

Trường hợp 2: x – 2 < 0 và x – 3 < 0

Ta có: x – 2 < 0 ⇔ x < 2

x – 3 < 0 ⇔ x < 3

Suy ra: x < 2

Vậy với x > 3 hoặc x < 2 thì (x - 2)/(x - 3) > 0

b. Trường hợp 1: x + 2 > 0 và x – 5 < 0

Ta có: x + 2 > 0 ⇔ x > -2

x – 5 < 0 ⇔ x < 5

Suy ra: -2 < x < 5

Trường hợp 2: x + 2 < 0 và x – 5 > 0

Ta có: x + 2 < 0 ⇔ x < -2

x – 5 > 0 ⇔ x > 5

Trường hợp trên không xảy ra.

Vậy với -2 < x < 5 thì (x + 2)/(x - 5) < 0.

Giải bài 88 trang 62 Toán tập 2 lớp 8 SBT

Chứng tỏ các phương trình sau vô nghiệm:

a. |2x + 3| = 2x + 2

b. |5x – 3| = 5x – 5

Lời giải:

a. Ta có: |2x + 3| = 2x + 3 khi 2x + 3 ≥ 0 ⇔ x ≥ -1,5

       |2x + 3| = -2x – 3 khi 2x + 3 < 0 ⇔ x < -1,5

Ta có: 2x + 3 = 2x + 2 ⇔ 0x = -1

Phương trình vô nghiệm.

       -2x – 3 = 2x + 2

       ⇔ -2x - 2x = 2 + 3

       ⇔ -4x = 5

       ⇔ x = -1,25

Giá trị x = -1,25 không thỏa mãn điều kiện x < -1,5 nên loại.

Vậy phương trình đã cho vô nghiệm.

b. Ta có: |5x – 3| = 5x – 3 khi 5x – 3 ≥ 0 ⇔ x ≥ 0,6

       |5x – 3| = 3 – 5x khi 5x – 3 < 0 ⇔ x < 0,6

Ta có: 5x – 3 = 5x – 5 ⇔ 0x = -2

Phương trình vô nghiệm.

       3 – 5x = 5x – 5

       ⇔ -5x – 5x = -5 – 3

       ⇔ -10x = -8

       ⇔ x = 0,8

Giá trị x = 0,8 không thỏa mãn điều kiện x < 0,6 nên loại.

Vậy phương trình đã cho vô nghiệm.

►► CLICK NGAY vào TẢI VỀ dưới đây để download hướng dẫn giải Sách bài tập Toán lớp 8 tập 2 trang 61, 62 file word, pdf hoàn toàn miễn phí.