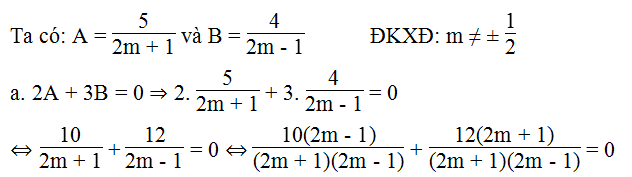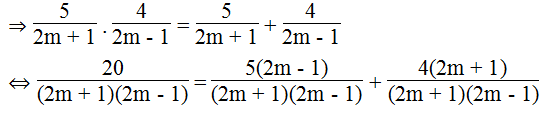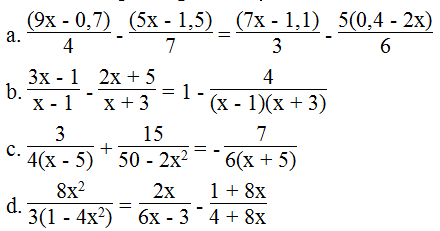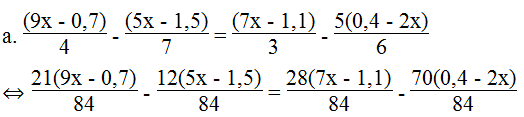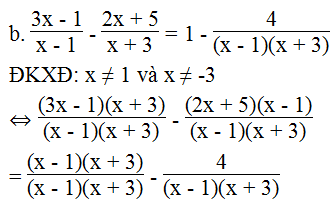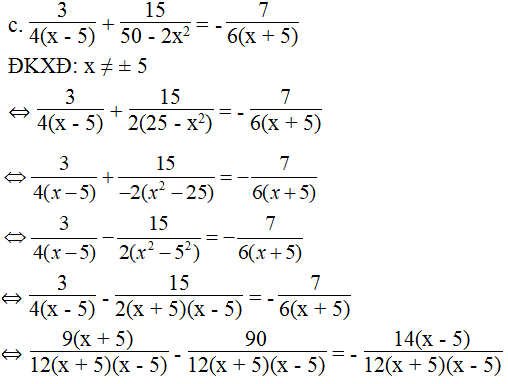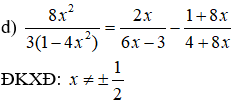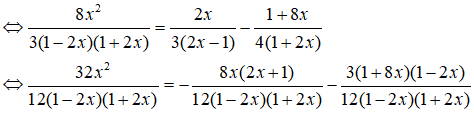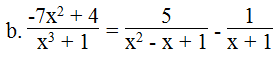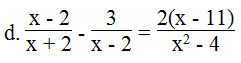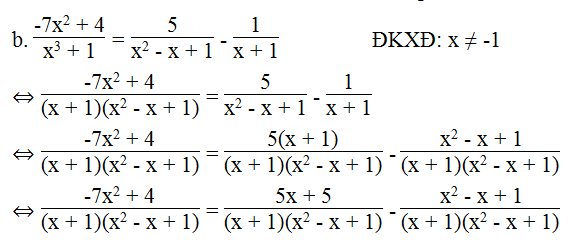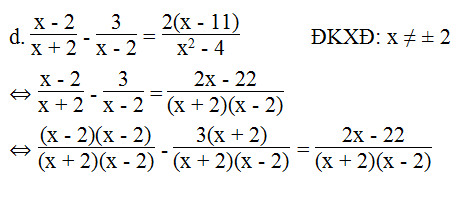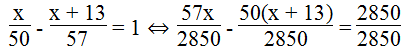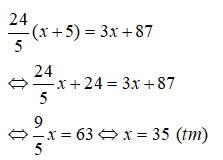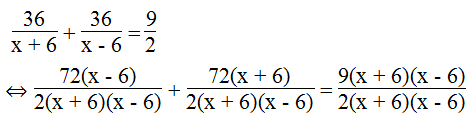Giải SBT Toán 8 trang 16, 17 tập 2 Bài: Ôn tập chương 3 - Phần Đại số

Lời giải Sách bài tập Toán lớp 8 tập 2 trang 16, 17 tập 2 Bài: Ôn tập chương 3 - Phần Đại số gồm các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải bài 62 Toán SBT tập 2 lớp 8 trang 16

Cho hai biểu thức A = 5/(2m + 1) và B = 4/(2m - 1) . Hãy tìm các giá trị của m để hai biểu thức ấy có giá trị thỏa mãn hệ thức:

a. 2A + 3B = 0

b. A.B = A + B

Lời giải:

⇔ 10(2m – 1) + 12(2m + 1) = 0

⇔ 20m – 10 + 24m + 12 = 0

⇔ 44m + 2 = 0

⇔ m = - 1/22 (thỏa)

Vậy m = - 1/22 thì 2A + 3B = 0.

b. A.B = A + B

⇔ 20 = 5(2m – 1) + 4(2m + 1)

⇔ 20 = 10m – 5 + 8m + 4

⇔ 18m = 21

⇔ m = 7/6 (thỏa)

Vậy m = 7/6 thì A.B = A + B

Giải bài 63 SBT Toán tập 2 lớp 8 trang 16

Tính gần đúng nghiệm của các phương trình sau, làm tròn đến chữ số thập phân thứ hai.

a. (x√13 + √5 )(√7 – x√3 ) = 0

b. (x√2,7 – 1,54)(√1,02 + x√3,1) = 0

Lời giải:

a. (x√13 + √5 )(√7 – x√3 ) = 0

⇔ x√13 + √5 = 0 hoặc √7 - x√3 = 0

x√13 + √5 = 0 ⇔ x = - √5 / √13 ≈ -0,62

√7 - x√3 = 0 ⇔ x = √7 / √3 ≈ 1,53

Vậy phương trình có nghiệm x = -0,62 hoặc x = 1,53

b. (x√2,7 – 1,54)(√1,02 + x√3,1) = 0

⇔ x√2,7 – 1,54 = 0 hoặc √1,02 + x√3,1 = 0

x√2,7 – 1,54 = 0 ⇔ x = 1,54/√2,7 ≈ 0,94

√1,02 + x√3,1 = 0 ⇔ x = - √1,02/√3,1 ≈ - 0,57

Vậy phương trình có nghiệm x = 0,94 hoặc x = - 0,57.

Giải bài 64 trang 16 Toán tập 2 lớp 8 SBT

Giải các phương trình sau:

Lời giải:

⇔ 21(9x – 0,7) – 12(5x – 1,5) = 28(7x – 1,1) – 70(0,4 – 2x)

⇔ 189x – 14,7 – 60x + 18 = 196x – 30,8 – 28 + 140x

⇔ 189x – 60x – 196x – 140x = - 30,8 – 28 + 14,7 – 18

⇔ - 207x = - 62,1 ⇔ x = 0,3

Vậy phương trình có nghiệm x = 0,3

⇔ (3x – 1)(x + 3) – (2x + 5)(x – 1) = (x – 1)(x + 3) – 4

⇔ 3x² + 9x – x – 3 – 2x² + 2x – 5x + 5 = x² + 3x – x – 3 – 4

⇔ 3x² – 2x² – x² + 9x – x + 2x – 5x – 3x + x = -3 – 4 + 3 – 5

⇔ 3x = - 9 ⇔ x = - 3 (loại)

Vậy phương trình vô nghiệm.

⇔ 9(x + 5) – 90 = - 14(x – 5) ⇔ 9x + 45 – 90 = - 14x + 70

⇔ 9x + 14x = 70 – 45 + 90 ⇔ 23x = 115 ⇔ x = 5 (loại)

Vậy phương trình vô nghiệm.

⇔ 32x² = - 8x(1 + 2x) – 3(1 + 8x)(1 – 2x)

⇔ 32x² = - 8x – 16x² – 3 – 18x + 48x²

⇔ 32x² + 16x² – 48x² + 18x + 8x = - 3

⇔ 26x = - 3 ⇔ x = - 3/26 (thỏa mãn)

Vậy phương trình có nghiệm x = - 3/26 .

Giải bài 65 lớp 8 SBT Toán tập 2 trang 16

Cho phương trình (ẩn x): 4x² – 25 + k² + 4kx = 0

a. Giải phương trình với k = 0

b. Giải phương trình với k = - 3

c. Tìm các giá trị của k sao cho phương trình nhận x = - 2 làm nghiệm

Lời giải:

a. Khi k = 0 ta có phương trình: 4x² – 25 = 0

⇔ (2x + 5)(2x – 5) = 0

⇔ 2x + 5 = 0 hoặc 2x – 5 = 0

2x + 5 = 0 ⇔ x = - 5/2

2x – 5 = 0 ⇔ x = 5/2

Vậy phương trình có nghiệm x = - 5/2 hoặc x = 5/2

b. Khi k = - 3 ta có phương trình: 4x² – 25 + (-3)² + 4(-3)x = 0

⇔ 4x² – 25 + 9 – 12x = 0

⇔ 4x² – 12x – 16 = 0

⇔ x² – 3x – 4 = 0

⇔ x² – 4x + x – 4 = 0

⇔ x(x – 4) + (x – 4) = 0

⇔ (x + 1)(x – 4) = 0

⇔ x + 1 = 0 hoặc x – 4 = 0

x + 1 = 0 ⇔ x = -1

x – 4 = 0 ⇔ x = 4

Vậy phương trình có nghiệm x = -1 hoặc x = 4.

c. Phương trình nhận x = -2 làm nghiệm nên ta có:

4(-2)² – 25 + k² + 4k(-2) = 0

⇔ 16 – 25 + k² – 8k = 0

⇔ k² – 8k – 9 = 0

⇔ k² – 9k + k – 9 = 0

⇔ k(k – 9) + (k – 9) = 0

⇔ (k + 1)(k – 9) = 0

⇔ k + 1 = 0 hoặc k – 9 = 0

k + 1 = 0 ⇔ k = -1

k – 9 = 0 ⇔ k = 9

Vậy k = -1 hoặc k = 9 thì phương trình nhận x = -2 làm nghiệm.

Giải bài 66 Toán SBT lớp 8 trang 17 tập 2

Giải các phương trình sau:

a. (x + 2)(x² – 3x + 5) = (x + 2)x²

c. 2x² – x = 3 – 6x

Lời giải:

a. (x + 2)(x² – 3x + 5) = (x + 2)x²

⇔ (x + 2)(x² – 3x + 5) – (x + 2)x² = 0

⇔ (x + 2)[(x² – 3x + 5) – x²] = 0

⇔ (x + 2)(x² – 3x + 5 – x²) = 0

⇔ (x + 2)(5 – 3x) = 0

⇔ x + 2 = 0 hoặc 5 – 3x = 0

x + 2 = 0 ⇔ x = -2

5 – 3x = 0 ⇔ x = 5/3

Vậy phương trình có nghiệm x = -2 hoặc x = 5/3

⇔ -7x² + 4 = 5x + 5 – x² + x – 1

⇔ -7x² + x² – 5x – x = 5 – 1 – 4

⇔ -6x² – 6x = 0

⇔ -x² – x = 0

⇔ x(x + 1) = 0

⇔ x = 0 hoặc x + 1 = 0

⇔ x = 0 hoặc x = -1 (loại)

Vậy phương trình có nghiệm x = 0.

c. 2x² – x = 3 – 6x

⇔ 2x² – x + 6x – 3 = 0

⇔ (2x² + 6x) – (x + 3) = 0

⇔ 2x(x + 3) – (x + 3) = 0

⇔ (2x – 1)(x + 3) = 0

⇔ 2x – 1 = 0 hoặc x + 3 = 0

2x – 1 = 0 ⇔ x = 1/2

x + 3 = 0 ⇔ x = -3

Vậy phương trình có nghiệm x = 1/2 hoặc x = -3

⇔ (x – 2)(x – 2) – 3(x + 2) = 2x – 22

⇔ x² – 2x – 2x + 4 – 3x – 6 = 2x – 22

⇔ x² – 2x – 2x – 3x – 2x + 4 – 6 + 22 = 0

⇔ x² – 9x + 20 = 0

⇔ x² – 5x – 4x + 20 = 0

⇔ x(x – 5) – 4(x – 5) = 0

⇔ (x – 4)(x – 5) = 0

⇔ x – 4 = 0 hoặc x – 5 = 0

x – 4 = 0 ⇔ x = 4

x – 5 = 0 ⇔ x = 5

Vậy phương trình có nghiệm x = 4 hoặc x = 5.

Giải bài 67 SBT Toán trang 17 tập 2 lớp 8

Số nhà của Khanh là một số tự nhiên có hai chữ số. Nếu thêm chữ số 5 vào bên trái số đó thì được một số kí hiệu là A. Nếu thêm chữ số 5 vào bên phải số đó thì được một số kí hiệu là B. Tìm số nhà của Khanh, biết rằng A - B = 153.

Lời giải:

Gọi x là, số nhà bạn Khanh. Điều kiện: x ∈N* và 9 < x < 100.

Thêm số 5 vào bên trái số nhà bạn Khanh ta được:

A = 5x−−−−−− = 500 + x

Thêm số 5 vào bên phải số nhà bạn Khanh ta được:

B = x5−−−−−− = 10x + 5

Vì hiệu của A - B = 153 nên ta có phương trình:

(500 + x) - (10x + 5) = 153 ⇔ 500 + x - 10x - 5 = 153

⇔ - 9x = 153 – 500 + 5 ⇔ - 9x = - 342 ⇔ x = 38 (thỏa mãn)

Vậy số nhà bạn Khanh là 38.

Giải bài 68 trang 17 tập 2 SBT Toán lớp 8

Một đội thợ mỏ lập kế hoạch khai thác than, theo đó mỗi ngày phải khai thác được 50 tấn than. Khi thực hiện, mỗi ngày đội khai thác được 57 tấn than. Do đó, đội đã hoàn thành kế hoạch trước một ngày và còn vượt mức 13 tấn than. Hỏi theo kế hoạch, đội phải khai thác bao nhiêu tấn than?

Lời giải:

Gọi x (tấn) là khối lượng than khai thác theo kế hoạch. ĐK: x > 0.

Thời gian dự định làm là x/50 (ngày)

Khối lượng than thực tế khai thác là x + 13 (tấn)

Thời gian thực tế làm là (x + 13)/57 (ngày)

Vì thời gian hoàn thành sớm hơn kế hoạch một ngày nên ta có phương trình:

⇔ 57x – 50x – 650 = 2850

⇔ 7x = 2850 + 650

⇔ 7x = 3500

⇔ x = 500 (thỏa)

Vậy theo kế hoạch, đội phải khai thác 500 tấn than.

Giải bài 69 Toán lớp 8 SBT trang 17 tập 2

Hai ô tô cùng khởi hành từ Lạng Sơn và Hà Nội, quãng đường dài 163km. Trong 43km đầu, hai xe cùng vận tốc. Nhưng sau đó chiếc xe thứ nhất tăng vận tốc lên gấp 1,2 lần vận tốc ban đầu, trong khi đó xe thứ hai vẫn duy trì vận tốc cũ. Do đó xe thứ nhất đến Hà Nội sớm hơn xe thứ hai là 40 phút. Tính vận tốc ban đầu của hai xe.

Lời giải:

Gọi x (km/h) là vận tốc ban đầu của hai xe. Điều kiện: x > 0.

Quãng dường còn lại sau khi xe thứ nhất tăng vận tốc là:

163 – 43 = 120 (km)

Vận tốc xe thứ nhất sau khi tăng tốc là 1,2x (km/h)

Thời gian xe thứ nhất đi hết quãng đường còn lại là 120/(1,2x) (giờ)

Thời gian xe thứ hai đi Hết quãng đường còn lại là 120/x (giờ)

Vì xe thứ nhất đến sớm hơn xe thú hai 40 phút = 2/3 giờ nên ta có phương trình:

120/x - 120/(1,2x) = 2/3

⇔ 120/x - 100/x = 2/3

⇔ 360/3x - 300/3x = 2x/3x

⇔ 360 – 300 = 2x

⇔ 2x = 60 ⇔ x = 30 (thỏa)

Vậy vận tốc ban đầu của hai xe là 30km/h.

Giải bài 70 trang 17 SBT lớp 8 Toán tập 2

Một đoàn tàu hỏa từ Hà Nội đi thành phố Hồ Chí Minh. 1 giờ 48 phút sau, một tàu hỏa khác khởi hành từ Nam Định đi thành phố Hồ Chí Minh với vận tốc nhỏ hơn vận tốc của đoàn tàu thứ nhất là 5km/h. Hai đoàn tàu gặp nhau (ở ga nào đó) sau 4 giờ 48 phút kể từ khi đoàn tàu thứ nhất khởi hành. Tính vận tốc của mỗi tàu biết rằng ga Nam Định nằm trên đường từ Hà Nội đi thành phố Hồ Chí Minh và cách Hà Nội 87km

Lời giải:

Gọi x (km/h) là vận tốc của đoàn tàu thứ hai. Điều kiện: x > 0.

Vận tốc của đoàn tàu thứ nhất là x + 5 (km/h)

Khi gặp nhau thì đoàn tàu thứ nhất đi được 4 giờ 48 phút.

Vì đoàn tàu thứ hai đi sau 1 giờ 48 phút nên đoàn tàu thứ nhất đi được 3 giờ

Thời gian đoàn tàu thứ nhất đi được khi hai tàu gặp nhau là:

4 giờ 48 phút = 24/5 giờ

Quãng đường đoàn tàu thứ hai đi được từ lúc khởi hành đến lúc hai đoàn tàu gặp nhau là 3x (km)

Quãng đường đoàn tàu thứ nhất đi được từ lúc khởi hành đến lúc hai đoàn tàu gặp nhau là 24/5 (x + 5) (km)

Theo để bài ta có phương trình:

Vận tốc của đoàn tàu thứ hai là 35km/h, vận tốc của đoàn tàu thứ nhất là 35 + 5 = 40 (km/h).

Giải bài 71 SBT Toán lớp 8 tập 2 trang 17

Lúc 7h sáng, một ca nô xuôi dòng từ bến A đến bến B, cách nhau 36km rồi ngay lập tức quay trở về bến A lúc 11 giờ 30 phút. Tính vận tốc của ca nô khi xuôi dòng biết rằng vận tốc của nước chảy là 6km/h.

Lời giải:

Gọi x (km/h) là vận tốc thực của ca nô. Điều kiện: x > 6

Vận tốc của ca nô khi xuôi dòng là x + 6 (km/h)

Vận tốc của ca nô khi ngược dòng là x – 6 (km/h)

Thời gian lúc ca nô đi xuôi dòng là 36/(x + 6) (giờ)

Thời gian lúc ca nô đi ngược dòng là 36/(x - 6) (giờ)

Thời gian ca nô đi và về:

11 giờ 30 phút – 7 giờ = 4 giờ 30 phút = 9/2 giờ

Theo đề bài, ta có phương trình:

⇔ 72(x – 6) + 72(x + 6) = 9(x + 6)(x – 6)

⇔ 72x – 432 + 72x + 432 = 9x² – 324

⇔ 9x² – 144x – 324 = 0

⇔ x² – 16x – 36 = 0

⇔ x² + 2x – 18x – 36 = 0

⇔ x(x + 2) – 18(x + 2) = 0

⇔ (x + 2)(x – 18) = 0

⇔ x + 2 = 0 hoặc x – 18 = 0

      x + 2 = 0 ⇔ x = -2 (loại)

      x – 18 = 0 ⇔ x = 18 (thỏa)

Vậy vận tốc thực của ca nô là 18km/h, suy ra vận tốc của ca nô lúc xuôi dòng là 18 + 6 = 24 (km/h).

►► CLICK NGAY vào TẢI VỀ dưới đây để download hướng dẫn giải Sách bài tập Toán lớp 8 tập 2 trang 16, 17 file word, pdf hoàn toàn miễn phí.