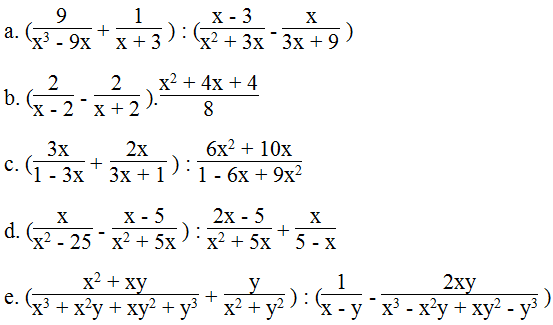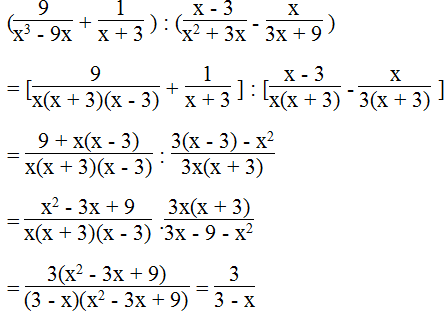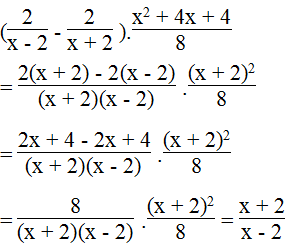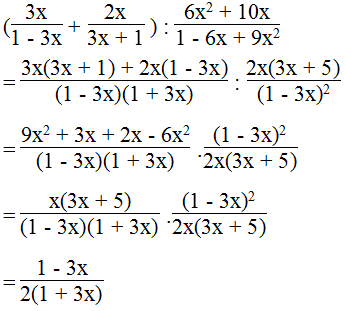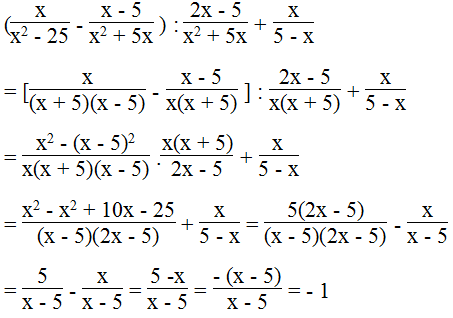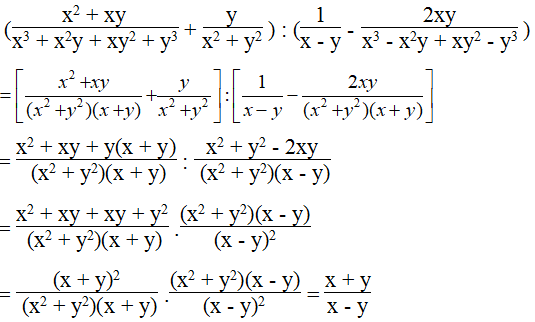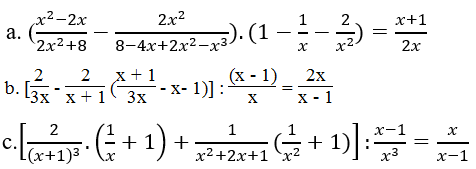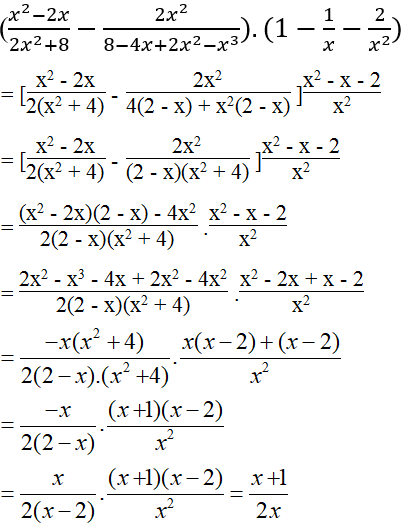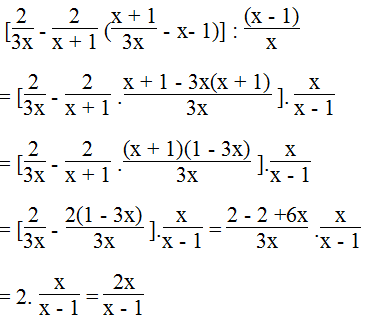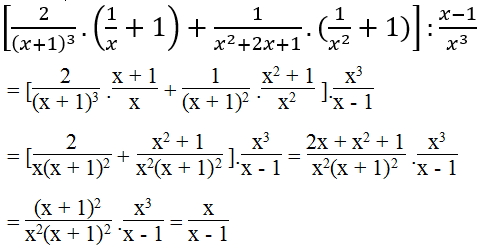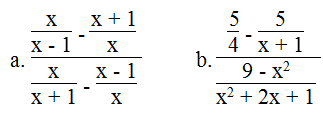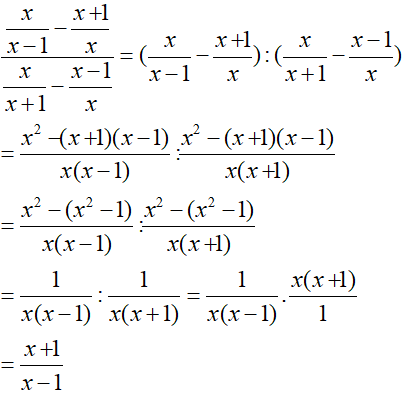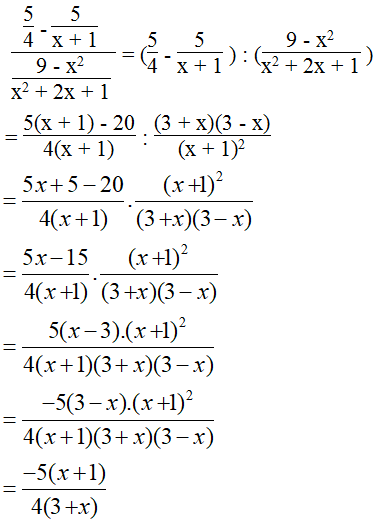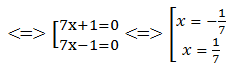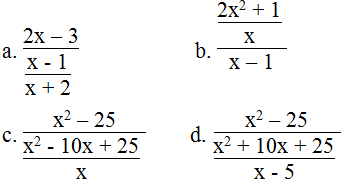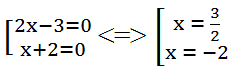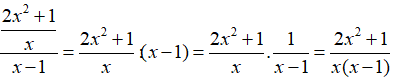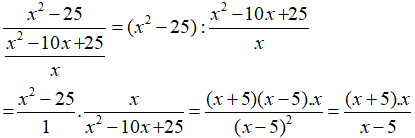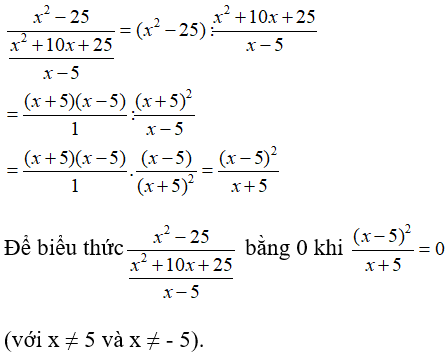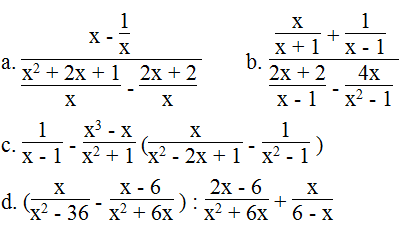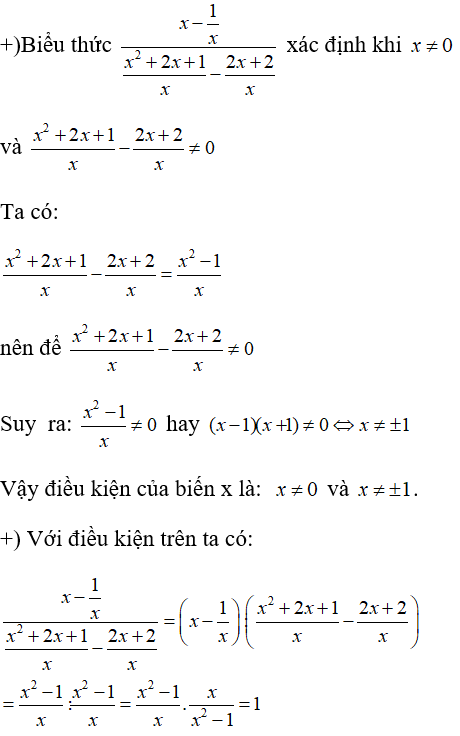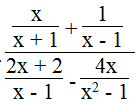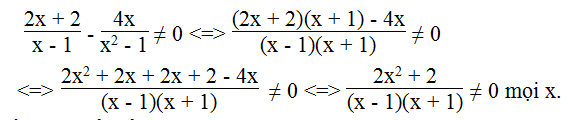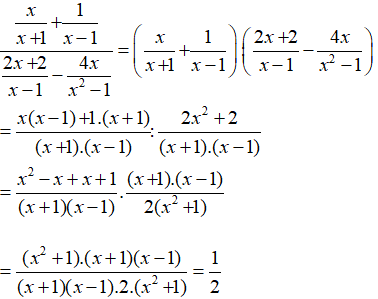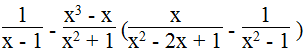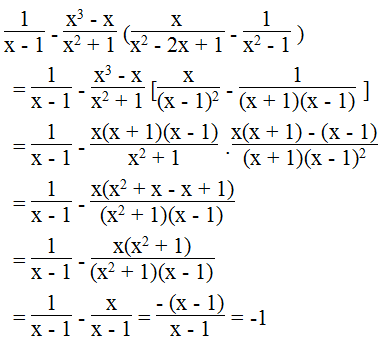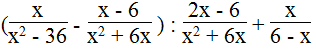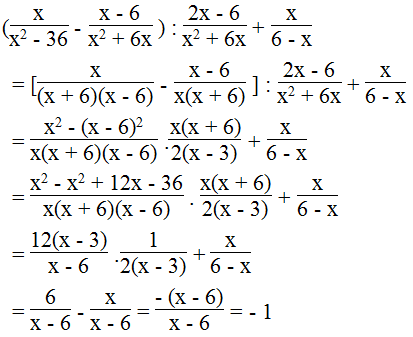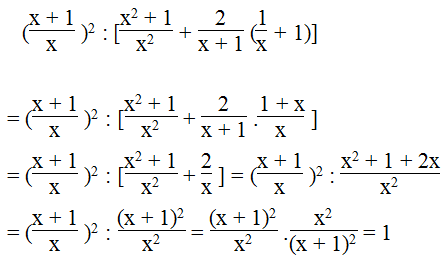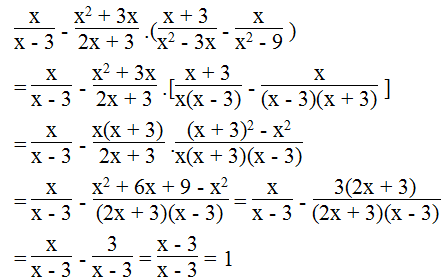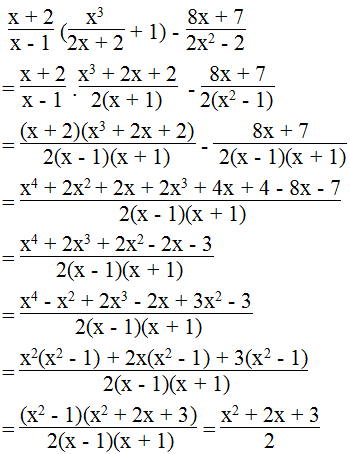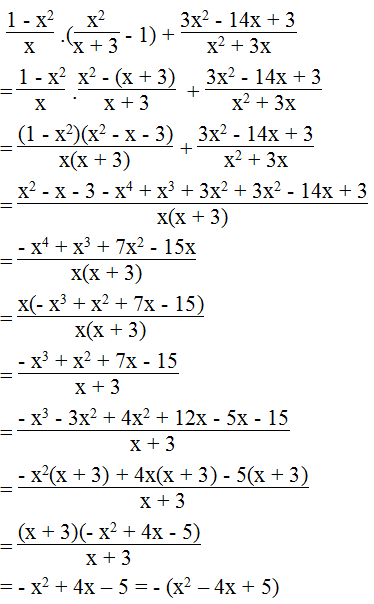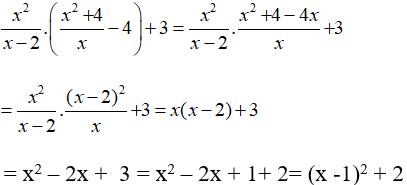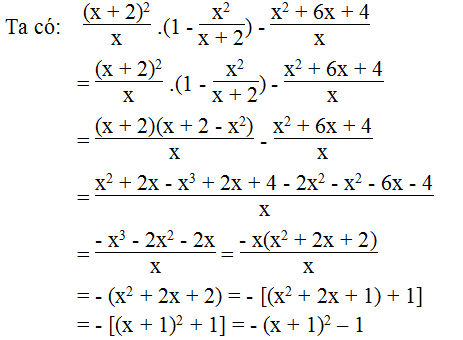Giải SBT Toán 8 trang 39, 40, 41, 42 tập 1 Bài: Ôn tập chương 2
Giải sách bài tập Toán 8 trang 39, 40, 41, 42 tập 1 Bài: Ôn tập chương 2 - Phân thức đại số được giải đáp chi tiết và rõ ràng nhất, giúp cho các bạn học sinh có thể tham khảo và chuẩn bị tốt nhất cho bài học sắp tới nhé.
Giải bài 58 SBT Toán lớp 8 tập 1 trang 39
Lời giải:
a.
b.
c.
d.
e.
Giải bài 59 trang 40 SBT lớp 8 Toán tập 1
Chứng minh đẳng thức:
Lời giải:
a. Ta có:
Vế trái bằng vế phải nên đẳng thức được chứng minh.
b. Ta có:
Vế trái bằng vế phải nên đẳng thức được chứng minh.
c. Ta có:
Giải bài 60 Toán lớp 8 SBT trang 40 tập 1
Biến đổi các biểu thức hữu tỉ thành phân thức:
Lời giải:
a.
b.
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Giải bài 61 trang 40 tập 1 SBT Toán lớp 8
Một phân thức có giá trị bằng 0 khi giá trị của tử thức bằng 0 còn giá trị của mẫu thức khác 0.Ví dụ giá trị của phân thức 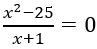
a.
b.
Lời giải:
a. Phân thức 
Ta có: x – 2 ≠ 0 ⇔ x ≠ 2
98x2 – 2 = 0 ⇔ 2(49x2 – 1) = 0 ⇔ (7x + 1)(7x – 1) = 0
Ta có: 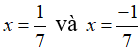
Vậy 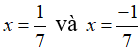

b. Phân thức 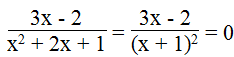
Ta có: (x+1)2 ≠ 0 ⇔ x+1 ≠ 0 ⇔ x ≠ - 1
3x – 2 = 0 ⇔
Ta có: 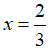
Vậy 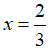
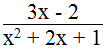
Giải bài 62 SBT Toán trang 40 tập 1 lớp 8
Đối với mỗi biểu thức sau, hãy tìm điều kiện của x để giá trị của biểu thức được xác định:
Lời giải:
a. Biểu thức 
x – 1 ≠ 0 và x + 2 ≠ 0 ⇔ x ≠ 1và x ≠ - 2
Vậy điều kiện để biểu thức xác định là x ≠ 1 và x ≠ - 2.
b. Biểu thức 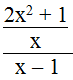
Vậy điều kiện để biểu thức xác định là x ≠ 0 và x ≠ 1.
c. Biểu thức 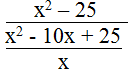
x2 – 10x + 25 ≠ 0 ⇔ (x – 5)2 ≠ 0 ⇔ x ≠ 5
Vậy điều kiện để biểu thức xác định là x ≠ 0 và x ≠ 5
d. Biểu thức 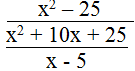
x2 + 10x + 25 ≠ 0 ⇔ (x + 5)2 ≠ 0 ⇔ x ≠ - 5
x – 5 ≠ 0 ⇔ x ≠ 5
Vậy điều kiện để biểu thức xác định là x ≠ 5 và x ≠ - 5.
Giải bài 63 Toán SBT lớp 8 trang 40 tập 1
Tìm giá trị của x để giá trị của các biểu thức trong bài tập 62 bằng 0.
Lời giải:
a. Biểu thức 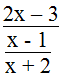
Ta có: 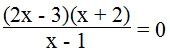
(2x – 3)(x + 2) = 0 ⇔
x – 1 ≠ 0 ⇔ x ≠ 1
x = - 2 không thỏa mãn điều kiện
Vậy x = 1,5 thì biểu thức 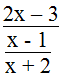
b. Biểu thức 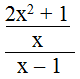
Ta có: 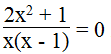
Ta có: 2x2 ≥ 0 nên 2x2 + 1 ≠ 0 mọi x.
Không có giá trị nào của x để biểu thức 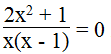
c. Biểu thức 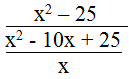
Ta có: 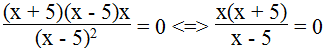
x(x + 5) = 0 ⇔ x = 0 hoặc x + 5 = 0 ⇔ x = - 5
x = 0 không thỏa mãn điều kiện.
Vậy x = - 5 thì biểu thức 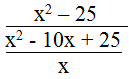
d. Biểu thức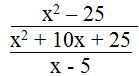
(x – 5)2 = 0 ⇔ x – 5 = 0 ⇔ x= 5
x = 5 không thỏa mãn điều kiện.
Vậy không có giá trị nào của x để biểu thức 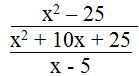
Giải bài 64 lớp 8 SBT Toán tập 1 trang 41
Tìm điều kiện của x để giá trị của biểu thức được xác định và chứng minh rằng với điều kiện đó biểu thức không phụ thuộc vào biến x:
Lời giải:
a.
Vậy với điều kiện x ≠ 0 và x ≠ ±1 thì biểu thức đã cho không phụ thuộc biến x.
b.
Ta có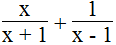
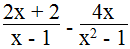
Vậy điều kiện để biểu thức xác định x ≠ ± 1
Ta có
Vậy với x ≠ ± 1 thì biểu thức đã cho không phụ thuộc vào x.
c.
Biểu thức xác định khi x – 1 ≠ 0, x2 – 2x + 1 ≠ 0 và x2 – 1 ≠ 0
x – 1 ≠ 0 ⇒ x ≠ 1
x2 – 2x + 1 ≠ 0 ⇒ (x – 1)2 ≠ 0 ⇒ x ≠ 1
x2 – 1 ≠ 0 ⇒ (x – 1)(x + 1) ≠ 0 ⇒ x ≠ -1 và x ≠ 1
Vậy biểu thức xác định với x ≠ -1 và x ≠ 1
Ta có:
Vậy biểu thức không phụ thuộc vào biến x.
d.
Biểu thức xác định khi x2 – 36 ≠ 0, x2 + 6x ≠ 0, 6 – x ≠ 0 và 2x – 6 ≠ 0
x2 – 36 ≠ 0 ⇒ (x – 6)(x + 6) ≠ 0 ⇒ x ≠ 6 và x ≠ -6
x2 + 6x ≠ 0 ⇒ x(x + 6) ≠ 0 ⇒ x ≠ 0 và x ≠ -6
6 – x ≠ 0 ⇒ x ≠ 6
2x – 6 ≠ 0 ⇒ x ≠ 3
Vậy x ≠ 0, x ≠ 3, x ≠ 6 và x ≠ -6 thì biểu thức xác định.
Ta có:
Vậy biểu thức không phụ thuộc vào biến x.
Giải bài 65 trang 41 Toán tập 1 lớp 8 SBT
Chứng minh rằng:
a. Giá trị của biểu thức 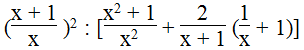
b. Giá trị của biểu thức 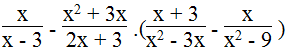
Lời giải:
a.
Biểu thức 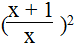
Biểu thức 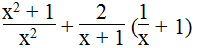
Với điều kiện x ≠ 0 và x ≠ - 1, ta có:
Vậy giá trị của biểu thức 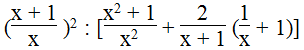
b. Biểu thức 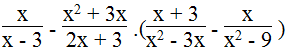
Suy ra: x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ 3 và x ≠ ± 3
Với điều kiện x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ - 3, ta có:
Vậy giá trị của biểu thức 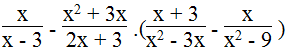
Giải bài 66 SBT Toán tập 1 lớp 8 trang 41
Chú ý rằng nếu c > 0 thì (a + b)2 + c và (a – b)2 + c đều dương với mọi a, b. Áp dụng điều này chứng minh rằng:
a. Với mọi giá trị của x khác ±1, biểu thức:
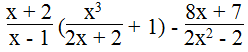
b. Với mọi giá trị của x khác 0 và khác – 3, biểu thức:
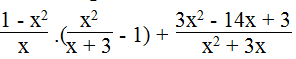
Lời giải:
a. Điều kiện x ≠ 1 và x ≠ - 1
Ta có:
Biểu thức dương khi x2 + 2x + 3 > 0
Ta có: x2 + 2x + 3 = x2 + 2x + 1 + 2 = (x + 1)2 + 2 > 0 với mọi giá trị của x.
Vậy giá trị của biểu thức dương với mọi giá trị x ≠ 1 và x ≠ - 1
b. Điều kiện x ≠ 0 và x ≠ -3
Ta có:
Vì x2 – 4x + 5 = x2 – 4x + 4 + 1 = (x – 2)2 + 1 > 0 với mọi giá trị của x nên
-x2 + 4x - 5 = -[(x – 2)2 + 1] < 0 với mọi giá trị của x.
Vậy giá trị biểu thức luôn luôn âm với mọi giá trị x ≠ 0 và x ≠ -3
Giải bài 67 SBT Toán lớp 8 tập 1 trang 42
Chú ý rằng vì (x + a)2 ≥ 0 với mọi giá trị của x và (x + a)2 =0 khi x = -a nên (x + a)2 + b ≥ 0 với mọi giá trị của x và (x + a)2 + b = b khi x = -a .Áp dụng điều này giải các bài tập sau:
a. Rút gọn rồi tìm giá trị của x để biểu thức 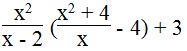
b. Rút gọn rồi tìm giá trị của x để biểu thức:
Lời giải:
a. Điều kiện x ≠ 2 và x ≠ 0
Vì (x – 1)2 ≥ 0 nên (x – 1)2 + 2 ≥ 2 với mọi giá trị của x.
Khi đó giá trị nhỏ nhất của biểu thức bằng 2 khi x = 1.
Vậy biểu thức đã cho có giá trị nhỏ nhất bằng 2 tại x = 1.
b. Điều kiện x ≠ -2 và x ≠ 0
Vì (x + 1)2 ≥ 0 nên –(x + 1)2 ≤ 0 ⇒ -(x + 1)2 – 1 ≤ -1
Khi đó biểu thức có giá trị lớn nhất bằng -1 khi x = -1
Vậy biểu thức đã cho có giá trị lớn nhất bằng -1 tại x = -1.
►► CLICK NGAY vào nút TẢI VỀ dưới đây để download Giải sách bài tập Toán lớp 8 tập 1 trang 39, 40, 41, 42 file word, pdf hoàn toàn miễn phí.
- Giải SBT Toán 8 trang 10 tập 1 bài 9 chi tiết nhất
- Giải SBT Toán 8 trang 56, 57, 58 tập 2 Bài 4 chi tiết nhất
- Giải SBT Toán 8 trang 51, 52, 53 tập 2 Bài 2 chi tiết nhất
- Giải SBT Toán 8 trang 6, 7 tập 2 Bài 2 chi tiết nhất
- Giải SBT Toán 8 trang 36, 37, 38 tập 1 Bài 9 chi tiết nhất
- Giải SBT Toán 8 trang 28, 29 tập 1 Bài 5: Phép cộng các phân thức đại số
- Giải SBT toán trang 11, 12 lớp 8 tập 1: Chia đơn thức cho đơn thức
- Giải SBT Toán 8 trang 14, 15 tập 2 Bài 6, 7 chi tiết nhất