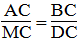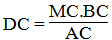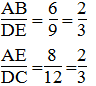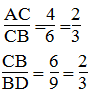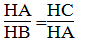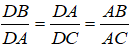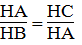Giải SBT Toán hình 8 trang 95, 96 tập 2 Bài 8 chính xác nhất

Lời giải Sách bài tập Toán lớp 8 tập 2 trang 95, 96 Bài 8: Các trường hợp đồng dạng của tam giác vuông gồm các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải bài 44 SBT Toán hình lớp 8 tập 2 trang 95

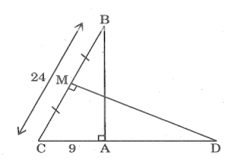
Cho tam giác ABC vuông tại A, AC = 9cm, BC = 24cm. Đường trung trực của BC cắt đường thẳng AC tại D, cắt BC tại M. Tính độ dài của đoạn thẳng CD.

Lời giải:

Xét hai tam giác vuông ABC và MDC, ta có:

∠(BAC) = ∠(DMC ) = 90°

∠C chung

Suy ra tam giác ABC đồng dạng với tam giác MDC (g.g)

Suy ra: 

Suy ra: 

Ta có: MC = 1/2 .BC = 1/2 .24 = 12 (cm)

Vây DC = (12.24)/9 = 32 (cm)

Giải bài 45 trang 95 SBT lớp 8 Toán hình tập 2

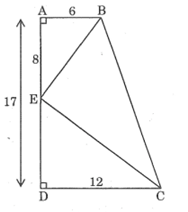
Cho hình thang vuông ABCD (∠A = ∠D = 90^o) AB = 6cm, CD = 12cm, AD = 17cm. Trên cạnh AD, đặt đoạn AE = 8cm. Chứng minh ∠(BEC) = 90^o

Lời giải:

Ta có: AD = AE + DE

Suy ra: DE = AD – AE = 17 – 8 = 9cm

Xét ΔABE và ΔDEC, ta có:

∠A = ∠D = 90^o (1)

Mà :

Suy ra: 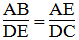 (2)

Từ (1) và (2) suy ra :ΔABE đồng dạng ΔDEC (c.g.c)

Suy ra: ∠ABE = ∠DEC

Trong ΔABE ta có: ∠A = 90^o ⇒ ∠(AEB) + ∠(ABE) = 90^o

Suy ra: ∠(AEB) + ∠(DEC) = 90^o

Lại có: ∠(AEB) + ∠(BEC) + ∠(DEC) = 180^o (kề bù)

Vậy : ∠(BEC) = 180^o- (∠(AEB) + ∠(DEC)) = 180^o - 90^o = 90^o

Giải bài 46 Toán hình lớp 8 SBT trang 95 tập 2

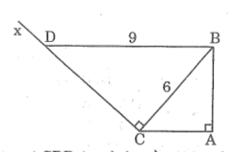
Cho tam giác ABC vuông tại A, AC =4cm, BC = 6cm. Kẻ tia Cx vuông góc với BC (tia Cx và điểm A khác phía so với đường thẳng BC). Lấy trên Cx điểm D sao cho BD =9cm. Chứng minh rằng BD // AC

Lời giải:

Xét hai tam giác vuông ABC và CDB, ta có:

∠(BAC) = ∠(DCB) = 90^o (1)

Mà:

Suy ra: 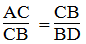 (2)

Từ (1) và (2) suy ra: ΔABC đồng dạng ΔCDB (cạnh huyền và cạnh góc vuông tỉ lệ)

Suy ra: ∠(ACB) = ∠(CBD)

⇒ BD//AC ( hai góc ở vị trí so le trong bằng nhau)

Giải bài 47 trang 95 tập 2 SBT Toán hình lớp 8

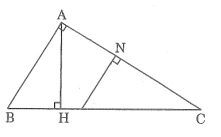
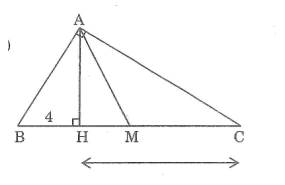
Trên hình vẽ hãy chỉ ra các tam giác đồng dạng .Viết các cặp tam giác đồng dạng theo thứ tự các đỉnh tương ứng và giải thích vì sao chúng đồng dạng

Lời giải:

-ΔABC đồng dạng ΔHBA

Hai tam giác vuông có góc nhọn ở đỉnh B chung

-ΔABC đồng dạng ΔHAC

Hai tam giác vuông có góc nhọn ở đỉnh C chung

-ΔABC đồng dạng ΔNMC

Hai tam giác vuông có góc nhọn ở đỉnh C chung

-ΔHAC đồng dạng ΔNMC

Hai tam giác vuông có góc nhọn ở đỉnh C chung

-ΔHAC đồng dạng ΔHBA

Hai tam giác vuông có góc nhọn ∠(HBA) = ∠(HAC)

-ΔHAB đồng dạng ΔNCM

Hai tam giác vuông có góc nhọn ∠(HAB) = ∠(NCM)

Giải bài 48 SBT Toán hình trang 95 tập 2 lớp 8

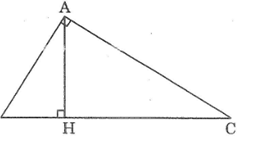
Cho tam giác ABC (∠A = 90^o) có đường cao AH. Chứng minh rằng AH² = BH.CH

Lời giải:

Xét hai tam giác vuông HBA và HAC, ta có:

∠(AHB) = ∠(AHC) = 90^o

∠B = ∠(HAC) (hai góc cùng phụ C )

Suy ra: ΔHBA đồng dạng ΔHAC (g.g)

Suy ra: 

Vậy AH² = BH.CH

Giải bài 49 Toán hình SBT lớp 8 trang 96 tập 2

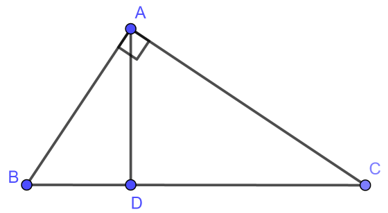
Đường cao của một tam giác vuông xuất phát từ đỉnh góc vuông chia cạnh huyền thành hai đoạn thẳng có dộ dài là 9cm và 16cm; Tính độ dài các cạnh của tam giác vuông.

Lời giải:

Xét hai tam giác vuông DAC và DBA ,ta có:

∠(ADC) = ∠(BDA) = 90^o

∠C = ∠(DAB) (hai góc cùng phụ ∠B )

Suy ra: ΔDAC đồng dạng ΔDBA (g.g)

Suy ra: 

⇒ DA² =DB.DC

hay DA = √(DB.DC) = √(9.16) = 12 (cm)

Áp dụng định lí Pi-ta-go vào tam giác vuông ABD, ta có:

AB² = DA² + DB² = 9² + 12² = 225 ⇒ AB =15 (cm)

Áp dụng định lí Pi-ta-go vào tam giác vuông ACD,ta có:

AC² = DA² + DC² = 12² +16² = 400 ⇒ AC = 20cm

Vậy BC = BD + DC = 9 + 16 = 25(cm)

Giải bài 50 lớp 8 SBT Toán hình tập 2 trang 96

Tam giác vuông ABC (A = 90^o) có đường cao AH và trung tuyến AM. Tính diện tích tam giác AMH,biết rằng BH = 4cm, CH = 9cm

Lời giải:

Xét hai tam giác vuông HBA,HAC có:

∠(BHA) = ∠(AHC) = 90^o

∠B = ∠(HAC) (hai góc cùng phụ ∠C )

⇒ΔHBA đồng dạng ΔHAC (g.g)

Suy ra: 

⇒ HA² = HB.HC = 4.9 = 36(cm)

Suy ra: AH = 6(cm)

Lại có: BM = 1/2 BC = 1/2 .(9+4) = 1/2 .13 = 6,5cm

Mà HM = BM – BH = 6,5 – 4 = 2,5cm

Vậy S_AHM = 1/2 AH.HN = 1/2 .6.2,5 = 7,5cm²

►► CLICK NGAY vào TẢI VỀ dưới đây để download hướng dẫn giải Sách bài tập Toán lớp 8 tập 2 trang 95, 96 bài 8: Các trường hợp đồng dạng của tam giác vuông, hỗ trợ tải file word, pdf hoàn toàn miễn phí.