Giải SBT Toán hình 8 trang 149, 150 tập 2 Bài 8 đầy đủ nhất
Lời giải Sách bài tập Toán hình lớp 8 tập 2 trang 149, 150 Bài 8: Diện tích xung quanh của hình chóp đều gồm các bài giải tương ứng với từng bài học trong sách bải tập giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.
Giải bài 58 SBT Toán hình lớp 8 tập 2 trang 149
Tính diện tích toàn phần của hình chóp tam giác đều theo các kích thước trên hình vẽ.
Lời giải:
Hình vẽ đã cho là hình chóp có 3 mặt xung quanh và mặt đáy là tam giác đều bằng nhau có cạnh là a.Áp dụng định lí pi-ta-go vào tam giác vuông CIA,ta có: AC2 = AI2 + CI2
Suy ra: CI2 = AC2 – AI2 = a2 – (a/2 )2 = 3a2/4
Vậy CI = a√3/2
Ta có: SABC =1/2. a .a√3/2 = (a2√3)/4 (đvdt)
Vậy STP =4. (a2√3)/4 = a2√3 (đvdt)
Giải bài 59 trang 150 SBT lớp 8 Toán hình tập 2
Cho hình chóp tứ giác đều. Điền số thích hợp vào ô còn lại trong bảng sau:
| Chiều cao (h) | 8 | 15 | ||
| Trung đoạn (l) | 10 | 15 | ||
| Cạnh đáy | 16 | 12 | 10 | |
| Sxq | 120 |
Lời giải:
| Chiều cao (h) | 8 | 15 | √189 | √11 |
| Trung đoạn (l) | 10 | 17 | 15 | 6 |
| Cạnh đáy | 12 | 16 | 12 | 10 |
| Sxq | 240 | 544 | 360 | 120 |
Giải bài 60 Toán hình lớp 8 SBT trang 150 tập 2
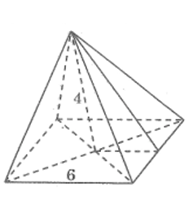
Một hình chóp tứ giác đều có độ dài cạnh đáy là = 6cm, chiều cao là 4cm thì diện tích xung quanh là:
A. 128 (cm2)
B. 96 (cm2)
C. 120 (cm2)
D.60 (cm2)
E. 84 (cm2)
Kết quả nào đúng?
Lời giải:
Kẻ trung đoạn của hình chóp.
Áp dụng định lí Pi-ta-go ta tính được trung đoạn của hình chóp bằng 5cm
Diện tích xung quanh của hình chóp là: Sxq = 4.1/2 .6,5 = 60 (cm2)
Vậy chọn đáp án D
Giải bài 61 trang 150 tập 2 SBT Toán hình lớp 8
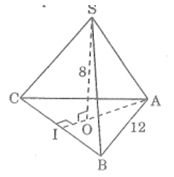
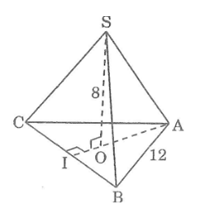
Hình chóp đều S.ABC có cạnh đáy bằng a=12cm,chiều cao h=8cm.Hãy tính diện tích xung quanh của hình chóp đó
Lời giải:
Kẻ AO kéo dài cắt BC tại I
Ta có: AI ⊥ BC (tính chất tam giác đều)
BI = IC = 1/2 BC
Áp dụng định lí pi-ta-go vào tam giác vuông AIB,ta có:
AB2 =BI2+AI2
Suy ra: AI2 = AB2- BI2 =122 -62=108
AI = √108 cm
Vì tam giác ABC đều nên O là trọng tâm của tam giác ABC
Ta có: OI = 1/3.AI = 1/3.√108 cm
Áp dụng định lí pi-ta-go vào tam giác vuông SOI ta có:
SI2= SO2 + OI2 = 8 + 1/9 .108 = 76
SI = √76 cm
Vậy Sxq = Pd= [(12.3):2]. √76 =18√76 cm
►► CLICK NGAY vào TẢI VỀ dưới đây để download hướng dẫn giải Sách bài tập Toán hình lớp 8 tập 2 trang 149, 150 bài 8: Diện tích xung quanh của hình chóp đều, hỗ trợ tải file word, pdf hoàn toàn miễn phí.
- Tổng hợp các dạng bài tập chương 1: Tứ giác lớp 8 có lời giải chi tiết
- Giải SBT Toán hình 8 trang 89, 90 tập 2 Bài 4 chi tiết nhất
- Giải SBT Toán hình 8 trang 91, 92, 93 tập 1 Bài 8: Đối xứng tâm hay nhất
- Giải SBT Toán hình 8 trang 161, 162 tập 1 Bài 4: Diện tích hình thang
- Giải SBT Toán hình 8 trang 157, 158, 159 tập 1 Bài 2 chính xác nhất
- Giải SBT Toán hình 8 trang 162, 163 tập 1 Bài 5: Diện tích hình thoi
- Giải SBT Toán hình 8 trang 95, 96 tập 1 Bài 10 chi tiết nhất
- Giải SBT Toán hình 8 trang 93, 94, 95 tập 1 Bài 9: Hình chữ nhật hay nhất