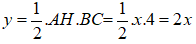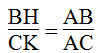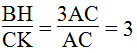Giải SBT Toán hình 8 trang 159, 160 tập 1 Bài 3: Diện tích tam giác
Giải sách bài tập Toán hình 8 trang 159, 160 tập 1 Bài 3: Diện tích tam giác được giải đáp chi tiết và rõ ràng nhất, giúp cho các bạn học sinh có thể tham khảo và chuẩn bị tốt nhất cho bài học sắp tới nhé.
Giải bài 25 SBT Toán hình lớp 8 tập 1 trang 159
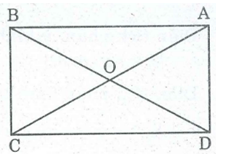
Hai đường chéo của hình chữ nhật chia hình chữ nhật thành bốn tam giác. Diện tích của các tam giác đó có bằng nhau không? Vì sao?
Lời giải:
Gọi O là giao điểm 2 đường chéo hình chữ nhật ABCD.
Ta có: OA = OB = OC = OD (tính chất hình chữ nhật)
ΔOAB = ΔOCD (c.g.c) ⇒ SOAB = SOCD (1)
ΔOAD = ΔOBC (c.g.c) ⇒ SOAD = SOBC (2)
Kẻ AH ⊥ BD
SOAD = 1/2 AH.OD
SOAB = 1/2 AH.OB
Suy ra: SOAD = SOAB (3)
Từ (1), (2) và (3) ⇒ SOAB = SOBC = SOCD = SODA
Giải bài 26 trang 159 SBT lớp 8 Toán hình tập 1
Cho tam giác ABC có đáy BC cố định và đỉnh A di động trên đường thẳng d cố định song song với BC. Chứng minh rằng tam giác ABC có diện tích không đổi.
Lời giải:
Đường thẳng d cố định song song với đường thẳng BC cố định nên khoảng cách hai đường thẳng d và BC là không đổi.
Tam giác ABC có cạnh đáy BC không đổi, chiều cao AH là khoảng cách giữa 2 đường thẳng song song không đổi.
Vậy điểm A thay đổi trên đường thẳng d // AB thì diện tích tam giác ABC không đổi.
Giải bài 27 Toán hình lớp 8 SBT trang 159 tập 1
Tam giác ABC có đáy BC cố định và dài 4cm. Đỉnh A di chuyển trên đường thẳng d ( d ⊥ BC). Gọi H là chân đường cao hạ từ đỉnh A đến đường thẳng BC.
a. Điền vào ô trống bảng sau:
| Độ dài AH (cm) | 1 | 2 | 3 | 4 | 5 | 10 | 15 | 20 |
| SABC (cm2) |
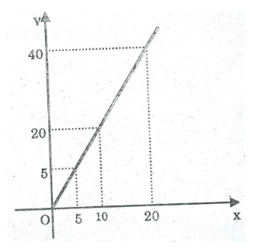
b. Vẽ đồ thị biểu diễn số đo SABC theo độ dài AH.
c. Diện tích tam giác tỉ lệ thuận với chiều cao AH không?
Lời giải:
a. Điền vào ô trống
| Độ dài AH (cm) | 1 | 2 | 3 | 4 | 5 | 10 | 15 | 20 |
| SABC (cm2) | 2 | 4 | 6 | 8 | 10 | 20 | 30 | 40 |
b. SABC là hàm số của chiều cao AH.
Gọi y là diện tích của ΔABC (cm2) và x là độ dài AH (cm) thì
Đồ thị như hình bên.
c. Diện tích của tam giác tỉ lệ thuận với chiều cao.
Giải bài 28 trang 160 tập 1 SBT Toán hình lớp 8
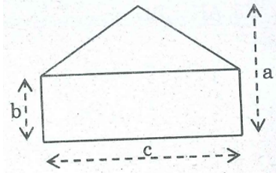
Tính diện tích hình bên theo kích thước đã cho trên hình.
Lời giải:
Diện tích phần là hình chữ nhật:
S1 = bc (đvdt)
Diện tích phần hình tam giác: (tam giác có chiều cao là a- b, cạnh đáy tương ứng là: c)
S2 = 1/2 c.(a- b) (đvdt)
Diện tích hình vẽ là: 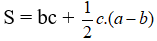
Giải bài 29 SBT Toán hình trang 160 tập 1 lớp 8
Hai cạnh của một tam giác có độ dài là 5cm và 6cm. Hỏi diện tích của tam giác đó có thể lấy giá trị nào trong các giá trị sau:
a. 10 cm2
b. 15 cm2
c. 20 cm2
Lời giải:
Giả sử hai cạnh của tam giác là 5 cm và 6 cm. Chiều cao tương ứng với hai cạnh của tam giác là h và k.
Ta có: S1 = 1/2 .5.h;
S2 = 1/2 .6.k
h và k là đường cao tương ứng với cạnh đáy là 5 và 6. Theo tính chất của đường vuông góc và đường xiên thì h ≤ 6 và k ≤ 5
Suy ra diện tích của tam giác S ≤ 15
Vậy diện tích của tam giác có thể bằng 10 cm2 hay 15 cm2 nhưng không thể bằng 20 cm2.
Giải bài 30 Toán hình SBT lớp 8 trang 160 tập 1
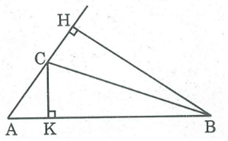
Cho tam giác ABC, biết AB = 3AC. Tính tỉ số hai đường cao xuất phát từ đỉnh B và C.
Lời giải:
Ta có: SABC = 1/2 AB.CK = 1/2 AC.BH
Suy ra: AB.CK = AC.BH ⇒
Mà AB = 3AC (gt) ⇒
Vậy đường cao BH dài gấp 3 lần đường cao CK.
Giải bài 31 lớp 8 SBT Toán hình tập 1 trang 160
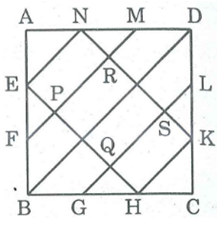
Các điểm E, F, G, H, K, L, M, N chia mỗi cạnh hình vuông ABCD có độ dài bằng 6cm thành ba đoạn thắng bằng nhau. Gọi P, Q, R, S là giao điểm của EH và NK với FM và GL. Tính diện tích của ngũ giác AEPSN và của tứ giác PQRS.
Lời giải:
Diện tích hình vuông ABCD bằng 6.6 = 36 (cm2)
Diện tích ΔBEH bằng 1/2 .4.4 = 8 (cm2)
Diện tích ΔDKN bằng 1/2 .4.4 = 8 (cm2)
Diện tích phần còn lại là: 36 - (8 + 8) = 20 (cm2)
Trong tam giác vuông AEN, ta có:
EN2 = AN2 + AE2 = 4 + 4 = 8 ⇒ EN = 2√2 (cm)
Trong tam giác vuông BHE, ta có:
EH2 = BE2 + BH2 = 16 + 16 = 32 ⇒ EH = 4√2 (cm)
Diện tích hình chữ nhật ENKH bằng: 2√2 . 4√2 = 16 (cm2)
Nối đường chéo BD. Theo tính chất đường thẳng song song cách đều ta có hình chữ nhật ENKH được chia thành 4 phần bằng nhau nên diện tích tứ giác PQRS chiếm 2 phần bằng 8 cm2
Diện tích ΔAEN bằng 1/2 .2.2 = 2 (cm2)
Vậy SAEPSN = SAEN + SEPSN = 2 + 16/4 = 6 (cm2)
►► CLICK NGAY vào nút TẢI VỀ dưới đây để download Giải sách bài tập Toán hình lớp 8 tập 1 trang 159, 160 file word, pdf hoàn toàn miễn phí.
- Tổng hợp các dạng bài tập chương 1: Tứ giác lớp 8 có lời giải chi tiết
- Giải SBT Toán hình 8 trang 89, 90 tập 2 Bài 4 chi tiết nhất
- Giải SBT Toán hình 8 trang 91, 92, 93 tập 1 Bài 8: Đối xứng tâm hay nhất
- Giải SBT Toán hình 8 trang 161, 162 tập 1 Bài 4: Diện tích hình thang
- Giải SBT Toán hình 8 trang 157, 158, 159 tập 1 Bài 2 chính xác nhất
- Giải SBT Toán hình 8 trang 162, 163 tập 1 Bài 5: Diện tích hình thoi
- Giải SBT Toán hình 8 trang 95, 96 tập 1 Bài 10 chi tiết nhất
- Giải SBT Toán hình 8 trang 93, 94, 95 tập 1 Bài 9: Hình chữ nhật hay nhất