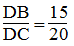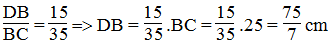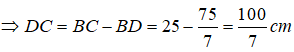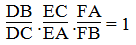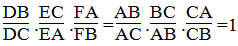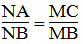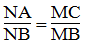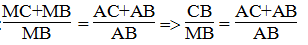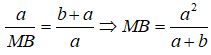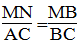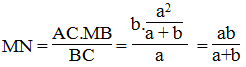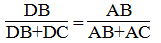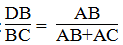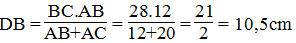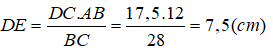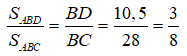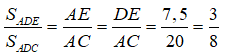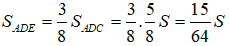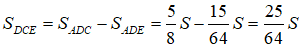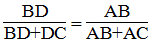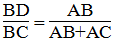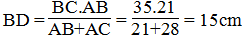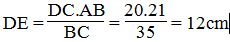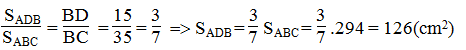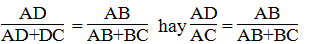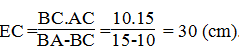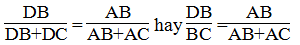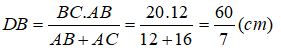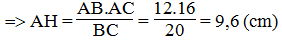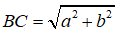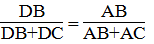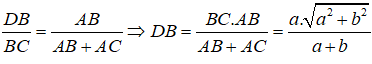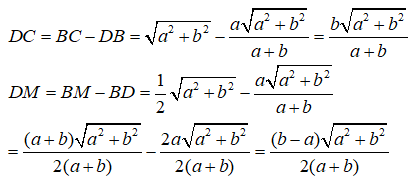Giải SBT Toán hình 8 trang 87, 88 tập 2 Bài 3 chi tiết nhất

Lời giải Sách bài tập Toán lớp 8 tập 2 trang 87, 88 tập 2 Bài 3: Tính chất đường phân giác của tam giác gồm các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải bài 17 SBT Toán hình lớp 8 tập 2 trang 87

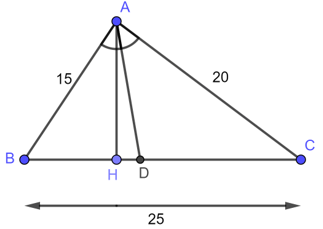
Tam giác ABC có AB = 15cm, AC = 20cm, BC = 25cm. Đường phân giác góc BAC cắt cạnh BC tại D.

a. Tính độ dài các đoạn thẳng DB và DC.

b. Tính tỉ số diện tích của hai tam giác ABD và ACD.

Lời giải:

Trong ΔABC, ta có: AD là đường phân giác của (BAC)

Suy ra: 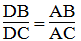 (tính chất đường phân giác)

Mà AB = 15 (cm); AC = 20 (cm)

Nên 

Suy ra: 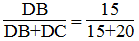 (tính chất tỉ lệ thức)

Suy ra: 

b. Kẻ AH ⊥ BC

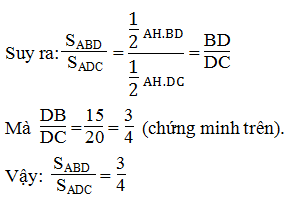
Ta có: S_ABD = 1/2 AH.BD; S_ADC = 1/2 AH.DC

Giải bài 18 trang 87 SBT lớp 8 Toán hình tập 2

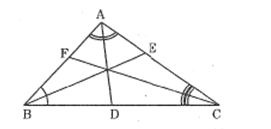
Tam giác ABC có các đường phân giác AD,BE,CF

Chứng minh rằng: 

Lời giải:

Trong ΔABC, ta có: AD là đường phân giác của ∠(BAC)

Suy ra: 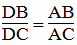 (tính chất đường phân giác) (1)

BE là đường phân giác của ∠(ABC)

Suy ra: 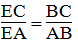 (tỉnh chất đường phân giác) (2)

CF là đường phân giác của ∠(ACB)

Suy ra: 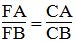 (tính chất đường phân giác) (3)

Nhân từng vế (1), (2) và (3) ta có:

Giải bài 19 Toán hình lớp 8 SBT trang 87 tập 2

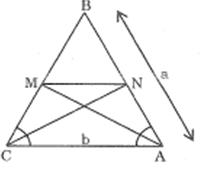
Tam giác cân ABC có BA = BC = a, AC = b.Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại N.

a. Chứng minh MN // AC

b. Tính MN theo a, b.

Lời giải:

a. Trong ΔBAC, ta có: AM là đường phân giác của (BAC)

Suy ra: 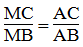 (tỉnh chất đường phân giác) (1)

CN là đường phân giác của (BCA)

Suy ra: 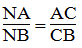 (tỉnh chất đường phân giác) (2)

Lại có: AB = CB = a (gt)

Từ (1), (2) và (gt) suy ra: 

Trong ΔBAC, ta có: 

Suy ra: MN // AC (theo định lí đảo của định lí Ta-lét).

Ta có: 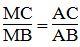 (chứng minh trên)

Suy ra:

Hay 

Trong ΔBAC, ta có:

MN //AC (chứng minh trên)

Và 

Vậy 

Giải bài 20 trang 87 tập 2 SBT Toán hình lớp 8

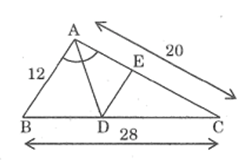
Tam giác ABC có AB= 12cm, AC = 20cm, BC= 28cm. Đường phân giác góc A cắt BC tại D. Qua D kẻ DE // AB (E ∈ AC).

a. Tính độ dài các đoạn thẳng BD, DC, DE.

b. Cho biết diện tích tam giác ABC là S,tính diện tích các tam ABD, ADE, DCE

Lời giải:

a. * Trong ΔABC, ta có:

AD là đường phân giác của ∠(BAC)

Suy ra: 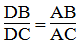 (tính chất tia phân giác)

Suy ra: 

Suy ra: 

Suy ra: 

Vậy DC = BC - DB = 28 - 10,5 = 17,5 (cm)

* Trong ΔABC, ta có: DE // AB

Suy ra: 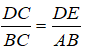 (Hệ quả định lí Ta-lét)

Vậy: 

b. Vì ΔABD và ΔABC có chung đường cao kẻ từ đỉnh A nên:

Vậy: S_ABD = 3/8.S

S_ADC = S_ABC - S_ABD = S - 3/8.S = 8/8.S - 3/8.S = 5/8.S

Vì DE // AB và AD là đường phân giác góc A nên AE = DE

Ta có: 

Vậy: 

Ta có: 

Giải bài 21 SBT Toán hình trang 88 tập 2 lớp 8

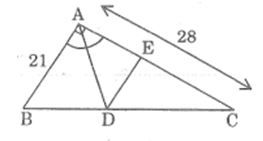
Cho tam giác ABC vuông tại A, AB = 21cm, AC = 28cm; đường phân giác góc A cắt BC tại D, đường thắng qua D song song với AB cắt AC tại E.

a.Tính độ dài các đoạn thẳng BD,DC và DE.

b. Tính diện tích tam giác ABD và diện tich tam giác ACD.

Lời giải:

a. Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:

BC² = AB² + AC² = 21² + 28² = 1225

Suy ra: BC = 35 (cm)

Vì AD là đường phân giác của ∠(BAC) nên:

 (t/chất đường phân giác)

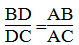
Suy ra: 

Hay 

Suy ra: 

Vậy DC = BC – BD = 35 – 15 = 20cm

Trong ΔABC ta có: DE // AB

Suy ra: 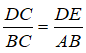 (Hệ quả định lí Ta-lét)

Suy ra: 

b. Ta có: S_ABC = 1/2.AB.AC = 1/2.21.28 = 294 (cm²)

Vì ΔABC và ΔADB có chung đường cao kẻ từ đỉnh A nên:

Vậy S_ADC = S_ABC – S_ABD = 294 – 126 = 168(cm²)

Giải bài 22 Toán hình SBT lớp 8 trang 88 tập 2

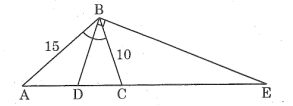
Cho tam giác cân ABC (AB = AC), đường phân giác góc B cắt AC tại D và cho biết AB = 15cm, BC = 10cm.

a. Tính AD, DC.

b. Đường vuông góc với BD tại B cắt đường thẳng AC tại E. Tính EC.

Lời giải:

Vì BD là đường phân giác của ∠(ABC) nên:

 (t/chất đường phân giác)

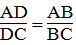
Suy ra:

Mà ΔABC cân tại A nên AC = AB = 15 (cm)

Suy ra: AD/15 = 15/(15+10) ⇒ AD = (15.15)/25 = 9(cm)

Vậy DC = AC – AD = 15 – 9 = 6 (cm)

b. Vì BE ⊥ BD nên BE là đường phân giác góc ngoài tại đỉnh B

Suy ra : 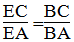 ( t/chất đường phân giác)

Suy ra:  ⇒ EC.BA= BC (EC + AC)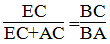

Suy ra: EC.BA - EC.BC = BC.AC ⇒EC (BA - BC) = BC.AC

Vậy 

Giải bài 23 lớp 8 SBT Toán hình tập 2 trang 88

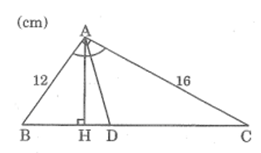
Tam giác ABC có góc A = 90^o, AB = 12cm, AC=16cm; đường phân giác góc A cắt BC tại D.

a. Tính BC, BD và DC.

b. Kẻ đường cao AH, tính AH, HD và AD.

Lời giải:

a. Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:

BC² = AB² + AC² = 12² + 16² = 400

Suy ra: BC =20 (cm)

Vì AD là đường phân giác của ∠(BAC) nên:

 (tính chất đường phân giác)

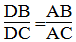
Suy ra: 

Suy ra: 

Vậy : DC = BC – DB = 20 - 60/7 = 80/7 (cm)

b. Ta có: S_ABC = 1/2.AB.AC = 1/2.AH.BC

Suy ra: AB.AC = AH.BC

Trong tam giác vuông AHB, ta có: ∠(AHB ) = 90^o

Theo định lí Pi-ta-go, ta có: AB² = AH² + HB²

Suy ra: HB² = AB² - AH² = 12² - (9,6)² = 51,84 ⇒ HB =7,2 (cm)

Vậy HD = BD – HB = 60/7 - 7,2 ≈ 1,37 (cm)

Trong tam giác vuông AHD, ta có: ∠(AHD) = 90^o

Theo định lí Pi-ta-go, ta có:

AD² = AH² + HD² = (9,6)² + (1,37)² = 94,0369

Suy ra: AD ≈ 9,70 (cm)

Giải bài 24 trang 88 Toán hình tập 2 lớp 8 SBT

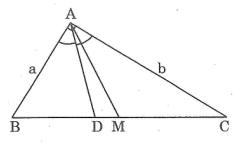
Tam giác ABC có ∠A = 90°, AB = a (cm), AC = b (cm) (a < b), trung tuyến AM, đường phân giác AD (M và D thuộc cạnh BC)

a. Tính độ dài các đoạn thẳng BC, BD, DC, AM và DM theo a, b

b. Hãy tính độ dài các đoạn thẳng trên chính xác đên chữ số thập phân thứ hai khi biết a = 4,15cm, b = 7,25cm.

Lời giải:

Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:

BC² = AB² + AC² = a² + b²

Suy ra:

Ta có: AM = BM = 1/2.BC (tính chất đường trung tuyến ứng với cạnh huyền).

Suy ra: AM = 1/2 √(a² + b²)

Vì AD là đường phân giác của ∠(BAC) nên:

 (tính chất đường phân giác)

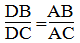
Suy ra: 

hay 

Vậy

b. Với a = 4,15 (cm); b = 7,25 (cm), sử dụng máy tỉnh, ta tính được:

BC = 8,35 cm

BD = 3,04 cm

DC ≈ 5,31 cm

AM ≈ 4,18 cm

DM ≈ 1,14cm

►► CLICK NGAY vào TẢI VỀ dưới đây để download hướng dẫn giải Sách bài tập Toán lớp 8 tập 2 trang 87, 88 file word, pdf hoàn toàn miễn phí.