Giải SBT Toán 8 trang 54, 55 tập 2 Bài 3: Bất phương trình một ẩn

Lời giải Sách bài tập Toán lớp 8 tập 2 trang 54, 55 tập 2 Bài 3: Bất phương trình một ẩn gồm các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải bài 31 SBT Toán lớp 8 tập 2 trang 54

Kiểm tra xem các giá trị sau đây của x có là nghiệm của bất phương trình x² – 2x < 3x

a. x = 2

b. x = 1

c. x = -3

d. x = 4

Lời giải:

a. Thay x = 2 vào bất phương trình ta được:

2² - 2.2 < 3.2 ( thỏa mãn)

Vậy x = 2 là nghiệm của bất phương trình

b. Thay x = 1 vào bất phương trình ta được:

1² - 2.1 < 3.1 ( thỏa mãn)

Vậy x = 1 là nghiệm của bất phương trình

c. Thay x = -3 vào bất phương trình ta được:

(-3)² - 2.(-3) < 3.(-3) ( không thỏa mãn)

Vậy x = -3 không là nghiệm của bất phương trình

d. Thay x = 4 vào bất phương trình ta được:

4² - 2.4 < 3.4 ( thỏa mãn)

Vậy x = 4 là nghiệm của bất phương trình

Giải bài 32 trang 54 SBT lớp 8 Toán tập 2

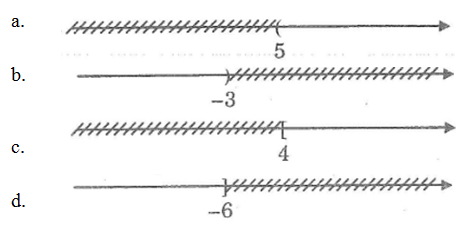
Biểu diễn tập nghiệm của bất phương trình sau trên trục số:

a. x > 5

b. x < -3

c. x ≥ 4

d. x ≤ -6

Lời giải:

Giải bài 33 Toán lớp 8 SBT trang 54 tập 2

Cho tập A = {-10; -9; -8; -7; -5; -4;……; 8; 9; 10}. Hãy cho biết giá trị nào của x trong tập A sẽ là nghiệm của bất phương trình.

a. |x| < 3

b. |x| > 8

c. |x| ≤ 4

d. |x| ≥ 7

Lời giải:

a. Ta có: |x| < 3 ⇔ -3 < x < 3

Các giá trị trong tập hợp A là nghiệm của bất phương trình là:

-2; -1; 0; 1; 2

b. Ta có: |x| > 8 ⇔ x > 8 hoặc x < -8

Các giá trị trong tập hợp A là nghiệm của bất phương trình là:

-10; -9; 9; 10

c. Ta có: |x| ≤ 4 ⇔ -4 ≤ x ≤ 4

Các số trong tập hợp A là nghiệm của bất phương trình là:

-4; -3; -2; -1; 0; 1; 2; 3; 4

d. Ta có: |x| ≥ 7 ⇔ x ≥ 7 hoặc x ≤ -7

Các số trong tập hợp A là nghiệm của bất phương trình là:

-10; -9; -8; -7; 7; 8; 9; 10

Giải bài 34 trang 54 tập 2 SBT Toán lớp 8

Hãy đưa ra hai sô nguyên là nghiệm của bất phương trình sau:

a. -4x + 5 > 10

b. 2x + 100 < 90

Lời giải:

a. Ta có: x = -4 và x = -3 là nghiệm của bất phương trình vì:

-4.(-4) + 5 = 16 + 5 = 21 > 10

-4.(-3) + 5 = 12 + 5 = 17 > 10

b. Ta có: x = -7 và x = -8 là nghiệm của bất phương trình vì:

2.(-7) + 100 = -14 + 100 = 86 < 90

2.(-8) + 100 = -16 + 100 = 84 < 90

Giải bài 35 SBT Toán trang 55 tập 2 lớp 8

Viết thành bất phương trình và chỉ ra một nghiệm của nó từ các mệnh đề sau đây:

a. Tổng của số nào đó và 5 lớn hơn 7.

b. Hiệu của 9 và số nào đó nhỏ hơn -12.

Lời giải:

a. x + 5 > 7

Ta có x = 3 là nghiệm của bất phương trình vì 3 + 5 = 8 > 7

b. 9 – x < -12

Ta có x = 22 là nghiệm của bất phương trình vì 9 – 22 = -13 < -12

Giải bài 36 Toán SBT lớp 8 trang 55 tập 2

Viết thành bất phương trình và chỉ ra hai nghiệm của nó từ các mệnh đề sau đây:

a. Tổng của 2 lần số nào đó và 3 lớn hơn 12.

b. Hiệu của 5 và 3 lần số nào đó nhỏ hơn 10.

Lời giải:

a. 2x + 3 > 12

Ta có: x = 6 và x = 7 là nghiệm của bất phương trình vì:

2.6 + 3 = 15 > 12 và 2.7 + 3 = 17 > 12

b. 5 – 3x < 10

Ta có: x = 1 và x = 2 là nghiệm của bất phương trình vì:

5 – 3.1 = 2 < 10 và 5 – 3.2 = -1 < 10

Giải bài 37 lớp 8 SBT Toán tập 2 trang 55

Cho tập A = {-10; -9; -8; -7;…..; 8; 9; 10}. Hãy cho biết số nào trong A là nghiệm của bất phương trình.

a. |x – 2| ≤ 3

b. |x – 3| > 5

Lời giải:

a. Ta có: |x – 2| ≤ 3

⇔ -3 ≤ x – 2 ≤ 3

⇔ -1 ≤ x ≤ 5

Các số trong tập hợp A là nghiệm của bất phương trình là:

-1; 0; 1; 2; 3; 4; 5

b. Ta có: |x – 3| > 5

⇒ (x-3 > 5) hoặc (x-3 < -5)

⇔ (x > 8) hoặc (x < -2)

Các số trong tập hợp A là nghiệm của bất phương trình là:

10; 9; -3; -4; -5; -6; -7; -8; -9; -10

Giải bài 38 SBT Toán tập 2 lớp 8 trang 55

Hãy đưa ra ba nghiệm của bất phương trình:

a. 5 > x

b. -4 < x

Lời giải:

a. Các số 3; 2; 1 là nghiệm của bất phương trình.

b. Các số -3; -2; -1 là nghiệm của bất phương trình.

Giải bài 39 trang 55 Toán tập 2 lớp 8 SBT

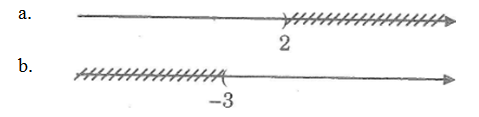
Viết tập hợp nghiệm của bất phương trình sau bằng kí hiệu tập hợp và biểu diễn tập nghiệm trên trục số.

a. 2 > x

b. -3 < x

Lời giải:

a. {x|x < 2}

b. {x|x > -3}

►► CLICK NGAY vào TẢI VỀ dưới đây để download hướng dẫn giải Sách bài tập Toán lớp 8 tập 2 trang 54, 55 file word, pdf hoàn toàn miễn phí.