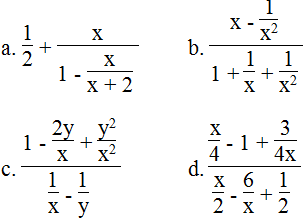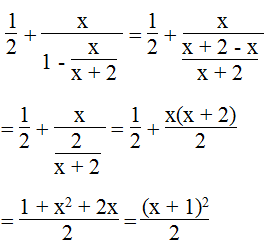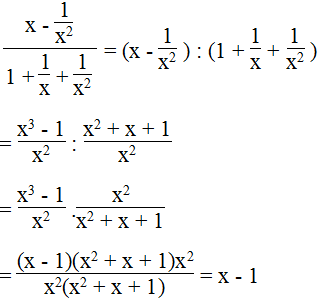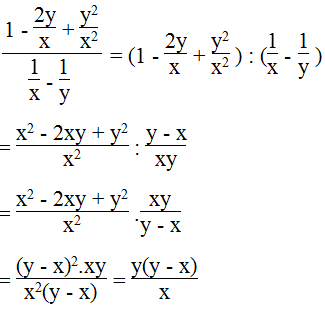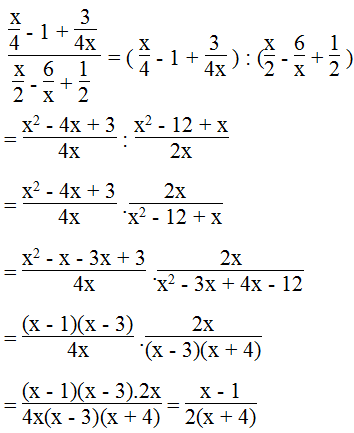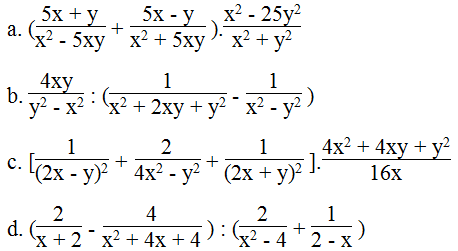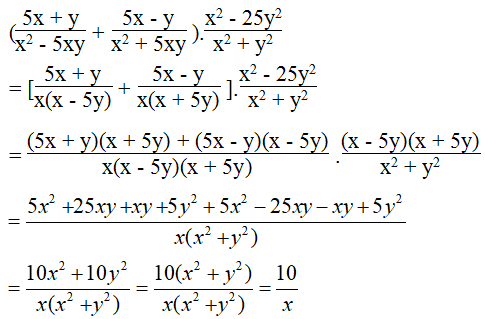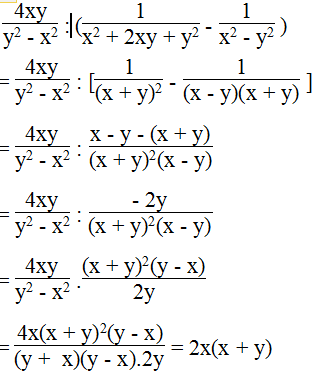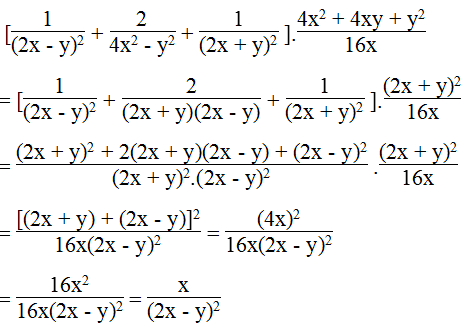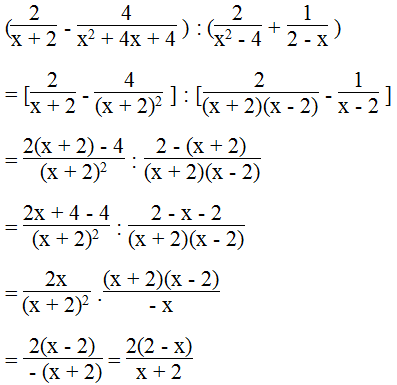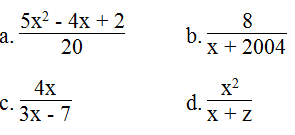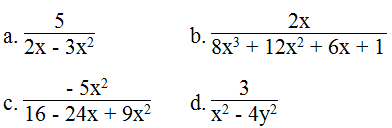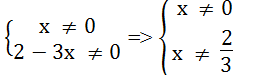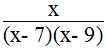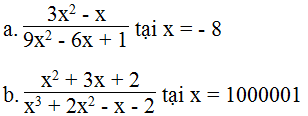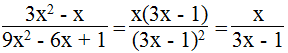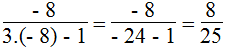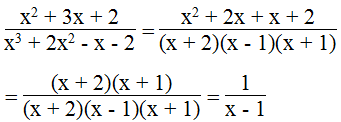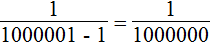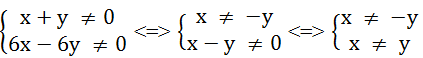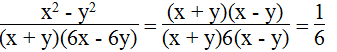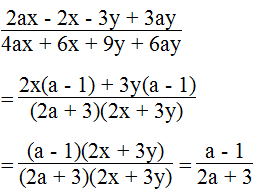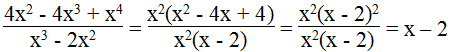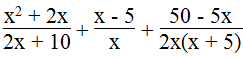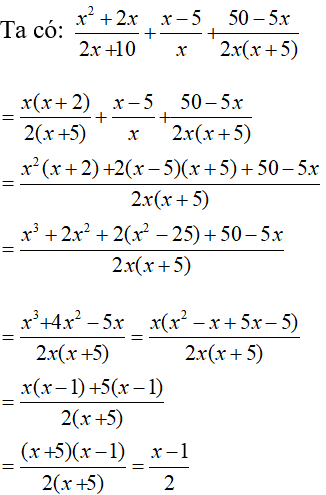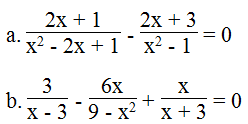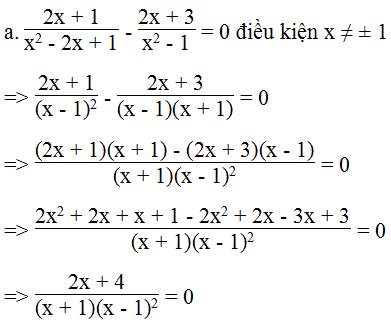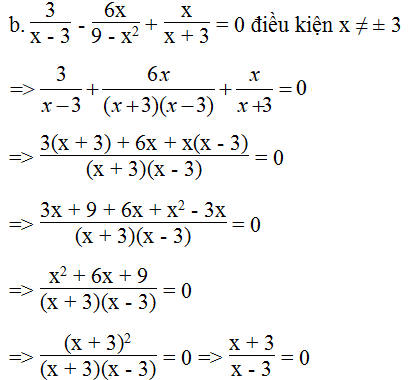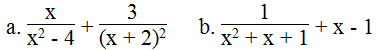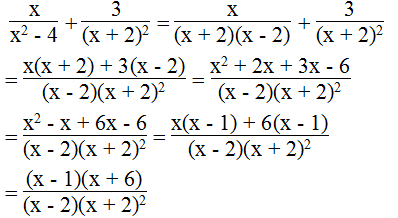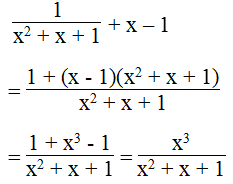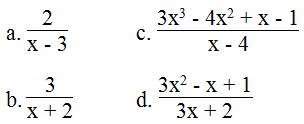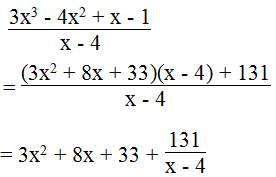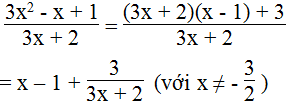Giải SBT Toán 8 trang 36, 37, 38 tập 1 Bài 9 chi tiết nhất

Giải sách bài tập Toán 8 trang 36, 37, 38 tập 1 Bài 9: Biến đổi các biểu thức hữu tỉ - Giá trị của phân thức được giải đáp chi tiết và rõ ràng nhất, giúp cho các bạn học sinh có thể tham khảo và chuẩn bị tốt nhất cho bài học sắp tới nhé.

Giải bài 44 SBT Toán lớp 8 tập 1 trang 36

Biến đổi các biểu thức sau thành phân thức:

Lời giải:

a.

b.

c.

d.

Giải bài 45 trang 36 SBT lớp 8 Toán tập 1

Thực hiện các phép tính sau:

Lời giải:

a.

b.

c.

d.

Giải bài 46 Toán lớp 8 SBT trang 36 tập 1

Tìm điều kiện của biến để giá trị của phân thức xác định:

Lời giải:

a. Phân thức: 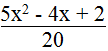xác định với mọi x ∈ R

b. Phân thức: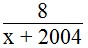xác định khi x + 2004 ≠ 0 ⇒ x ≠ - 2004

c. Phân thức: 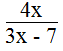xác định khi 3x – 7 ≠ 0 ⇒ x ≠ 7/3

d. Phân thức: 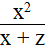xác định khi x + z ≠ 0 ⇒ x ≠ - z

Giải bài 47 trang 36 tập 1 SBT Toán lớp 8

Phân tích mẫu thức của các phân thức sau thành nhân tử rồi tìm điều kiện của x để giá trị của phân thức xác định:

Lời giải:

a. 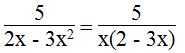xác định khi:

x(2 – 3x) ≠ 0 ⇔ 

Vậy phân thức 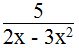 xác định với x ≠ 0 và x ≠ 2/3

b.  xác định khi (2x + 1)³ ≠ 0

Suy ra: 2x + 1 ≠ 0 ⇒ x ≠ - 1/2

c. 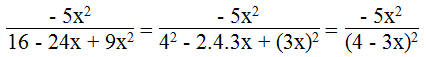 xác định khi:

(4 – 3x)² ≠ 0 ⇒ 4 – 3x ≠ 0 ⇒ x ≠ 4/3

d. 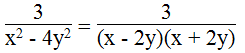 xác định khi:

(x – 2y)(x + 2y) ≠ 0 ⇔ 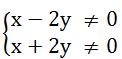 ⇒ x ≠ ± 2y

Giải bài 48 SBT Toán trang 37 tập 1 lớp 8

Có bạn nói rằng các phân thức 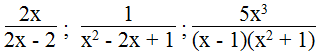có cùng điều kiện biến x. Điều đó đúng hay sai? Vì sao?

Lời giải:

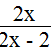
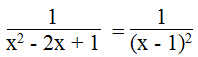
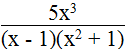
Ta có: xác định khi 2x – 2 ≠ 0 ⇒ 2x ≠ 2 ⇒ x ≠ 1

xác định khi (x – 1)² ≠ 0 ⇒ x – 1 ≠ 0 ⇒ x ≠ 1

 xác định khi (x – 1)(x² + 1) ≠ 0 hay x – 1 ≠ 0

( vì với mọi x thì x² ≥ 0 nên x² + 1 > 0)

Do đó, phân thức 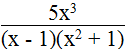 xác định với x ≠ 1.

Vậy các phân thức 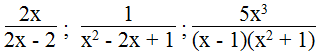có cùng điều kiện biến x là đúng.

Giải bài 49 Toán SBT lớp 8 trang 37 tập 1

a. Tìm một phân thức (một biến) mà giá trị của nó xác định với mọi giá trị của biến khác các số nguyên lẻ lớn hơn 5 và nhỏ hơn 10.

b. Tìm một phân thức (một biến) mà giá trị của nó xác định với mọi giá trị của biến khác ± √2

Lời giải:

a

+) Tập hợp các số nguyên lẻ lớn hơn 5 và nhỏ hơn 10 là: { 7; 9}.

+) Do đó, phân thức cần tìm xác định với x ≠ 7; x ≠ 9 . Suy ra: x – 7 ≠ 0 và x – 9 ≠ 0

Ta chọn phân thức là 

b. Phân thức một biến màgiá trị của nó được xác định với mọi giá trị của biến khác ± √2 => x ≠ √2 và x ≠ - √2

Suy ra: x - √2 ≠ 0 và x + √2 ≠ 0 ta chọn phân thức:

(với a là một hằng số)

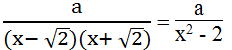
Giải bài 50 lớp 8 SBT Toán tập 1 trang 37

Đố em tìm được một cặp phân thức của biến x mà khi giá trị của phân thức này bằng 0 thì giá trị của phân thức kia không xác định và ngược lại khi giá trị phân thức kia bằng 0 thì giá trị phân này không xác định. Em tìm được bao nhiêu cặp như thế?

Lời giải:

Ta chỉ cần tìm hai phân thức là nghịch đảo của nhau.

Ví dụ: 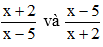. Có vô số cặp phân thức như vậy.

Có vô số cặp phân thức như vậy.

Giải bài 51 trang 37 Toán tập 1 lớp 8 SBT

Tìm giá trị của các biểu thức:

Lời giải:

a. 9x² – 6x + 1 ≠ 0 ⇒ (3x – 1)² ≠ 0 ⇒ x ≠ 1/3 ta có x = - 8 ≠ 1/3

Thay x = - 8 vào biểu thức, ta có: 

b. Ta có: x³ + 2x² – x – 2 = x²(x + 2) – (x + 2) = (x² -1). (x+ 2) = (x +1).(x-1)(x+ 2)

Do đó, để x³ + 2x² – x - 2 ≠ 0 khi (x + 2)(x – 1)(x + 1) ≠ 0 ⇒ x ≠ - 2 và x ≠ ± 1

Ta có: x = 1000001 thỏa mãn điều kiện.

Thay x = 1000001 vào biểu thức ta được: 

Giải bài 52 SBT Toán tập 1 lớp 8 trang 37

Tìm điều kiện của các biến trong mỗi phân thức sau đây. Chứng minh rằng khi giá trị của phân thức xác định thì giá trị đó không phụ thuộc vào các biến x và y (nghĩa là chứng tỏ rằng có thể biến đổi phân thức đã cho thành một biểu thức không chứa x và y)

a. 

b. 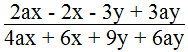(a là hằng số khác - 3/2 )

Lời giải:

a. 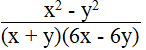xác định khi:

(x + y)(6x – 6y) ≠ 0 ⇒ 

Điều kiện x ≠ ± y

Vậy biểu thức không phụ thuộc vào x, y.

b. 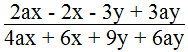xác định khi 4ax + 6x + 9y + 6ay ≠ 0

⇒ 2x(2a + 3) + 3y(2a + 3) = (2a + 3)(2x + 3y) ≠ 0

Ta có: 2a + 3 ≠ 0 ⇒ a ≠ - 3/2 ; 2x + 3y ≠ 0 ⇒ x ≠ - 3/2 y

Điều kiện: x ≠ - 3/2 y và a ≠ - 3/2

Vậy biểu thức không phụ thuộc vào x, y.

Giải bài 53 Toán SBT trang 37 tập 1 lớp 8 

Đố em tìm được giá trị của x để giá trị của phân thức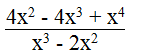bằng:

a. – 2            b. 2            c. 0

Lời giải:

Điều kiện: x³ – 2x² = x²(x – 2) ≠ 0 ⇒ x ≠ 0 và x ≠ 2

Ta có: 

a. Nếu phân thức đã cho bằng -2 thì biểu thức x - 2 cũng có giá trị bằng -2. Suy ra: x - 2 = -2 ⇒ x = 0 không thỏa mãn điều kiện.

Vậy không có giá trị nào của x để phân thức bằng -2

b. Nếu phân thức đã cho bằng 2 thì biểu thức x - 2 cũng có giá trị bằng 2. Suy ra: x- 2 = 2 ⇒ x = 4. Với x = 4 thỏa mãn điều kiện.

Vậy khi x = 4 thì phân thức có giá trị bằng 2.

c. Nếu phân thức có giá trị bằng 0 thì biểu thức x - 2 cũng có giá trị bằng 0. Suy ra: x - 2 = 0 ⇒ x = 2 mà x = 2 không thỏa mãn điều kiện.

Vậy không có giá trị nào của x để phân thức có giá trị bằng 0.

Giải bài 54 SBT Toán lớp 8 tập 1 trang 37

Cho biểu thức 

a. Tìm điểu kiện của biến x để giá trị của biểu thức được xác định.

b. Tìm giá trị của x để giá trị của biểu thức bằng 1.

c. Tìm giá trị của x để giá trị của biểu thức bằng - 1/2

d. Tìm giá trị của x để giá trị của biểu thức bằng -3

Lời giải:

a. Biểu thức xác định khi 2x + 10 ≠ 0, x ≠ 0 và 2x(x + 5) ≠ 0

Điều kiện x ≠ 0 và x ≠ - 5

b. Nếu giá trị phân thức bằng 1 thì giá trị của biểu thức (x - 1) / 2 cũng bằng 1.

Suy ra: (x - 1) / 2 = 1 ⇒ x – 1 = 2 ⇒ x = 3 mà x = 3 thỏa mãn điều kiện.

Vậy x = 3 thì giá trị của phân thức bằng 1.

c. Nếu giá trị phân thức bằng - 1/2 thì giá trị của biểu thức (x - 1) / 2 cũng bằng - 1/2.

Suy ra: (x - 1) / 2 = - 1/2 ⇒ x – 1 = - 1 ⇒ x = 0 mà x = 0 không thỏa mãn điều kiện.

Vậy không có giá trị nào của x để phân thức bằng - 1/2 .

d. Nếu giá trị phân thức bằng – 3 thì giá trị của biểu thức (x - 1) / 2 cũng bằng - 3.

Suy ra: (x - 1) / 2 = -3 ⇒ x – 1 = -6 ⇒ x = -5 mà x = -5 không thỏa mãn điều kiện.

Vậy không có giá trị nào của x để phân thức bằng -3.

Giải bài 55 trang 38 SBT lớp 8 Toán tập 1

Tìm x, biết:

Lời giải:

Biểu thức bằng 0 khi tử bằng 0 và mẫu khác 0

Ta có: 2x + 4 = 0 => x = - 2 (thỏa mãn điều kiện)

Vậy với x = - 2 thì giá trị của biểu thức bằng 0.

Biểu thức bằng 0 khi tử bằng 0 và mẫu khác 0

Ta có: x + 3 = 0 => x = -3 (không thỏa mãn điều kiện)

Vậy không có giá trị nào của x để biểu thức bằng 0.

Giải bài 56 Toán lớp 8 SBT trang 38 tập 1

Với giá trị nào của x thì giá trị của mỗi biểu thức sau bằng 0:

Lời giải:

a. Biểu thức xác định khi: x² – 4 = (x+ 2).(x- 2) ≠ 0 và (x + 2)² ≠ 0 hay x ≠ ± 2 .

Ta có:

Biểu thức bằng 0 khi (x – 1)(x + 6) = 0 và (x – 2)(x + 2)² ≠ 0

+) Ta có: (x - 1).(x + 6) = 0 khi x - 1= 0 hay x + 6 = 0

x - 1 = 0 khi x = 1 ( thỏa mãn điều kiện)

x + 6 = 0 khi x = -6 ( thỏa mãn điều kiện)

Vậy với x = 1 hoặc x = - 6 thì giá trị biểu thức bằng 0.

b.

Biểu thức bằng 0 khi x³ = 0 và x² + x + 1 ≠ 0

Ta có: x³ = 0 ⇒ x = 0;

x² + x + 1 = x² + 2.x.1/2 + 1/4 + 3/4 = (x+ 1/2 )² + 3/4 ≠ 0 mọi x.

Vậy với x = 0 thì giá trị của biểu thức bằng 0.

Giải bài 57 trang 38 tập 1 SBT Toán lớp 8

Tìm giá trị nguyên của biến x để tại đó giá trị của mỗi biểu thức sau là một số nguyên:

Lời giải:

a. Vì 2 / (x - 3) là một số nguyên nên 2 ⋮ (x – 3) và x ≠ 3

Suy ra: x – 3 ∈ Ư(2) = {- 2; - 1; 1; 2}

Ta có:x – 3 = - 2 ⇒ x = 1;            x – 3 = - 1 ⇒ x = 2

      x – 3 = 1 ⇒ x = 4;            x – 3 = 2 ⇒ x = 5

Vậy với x ∈ {1; 2; 4; 5} thì 2 / (x - 3) là một số nguyên.

b. Vì 3 / (x + 2) là một số nguyên nên 3 ⋮ (x + 2) và x ≠ - 2

Suy ra: x + 2 ∈ Ư(3) = {- 3; - 1; 1; 3}

Ta có: x + 2 = - 3 ⇒ x = - 5;            x + 2= - 1 ⇒ x = - 3

      x + 2 = 1 ⇒ x = -1;            x + 2 = 3 ⇒ x = 1

Vậy với x ∈ {-5; -3; -1; 1} thì 3 / (x + 2) là một số nguyên.

c. Ta có:

Với x là số nguyên ta có: 3x² + 8x + 33 là số nguyên.

Để biểu thức đã cho là số nguyên thì 131 ⋮ (x – 4) và x ≠ 4

Suy ra: x – 4 ∈ Ư(131) = {-131; -1; 1; 131}

Ta có: x – 4 = -131 ⇒ x = -127;            x – 4 = -1 ⇒ x = 3

      x – 4 = 1 ⇒ x = 5;            x – 4 = 131 ⇒ x = 135

Vậy với x ∈ {-127; 3; 5; 135} thì 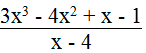là số nguyên.

d. Ta có:

Vì x là số nguyên nên x – 1 là số nguyên.

Để biểu thức đã cho là số nguyên thì 3 ⋮ (3x + 2) và x ≠ -2/3

Suy ra: 3x + 2 ∈ Ư(3) = {-3; -1; 1; 3}

Ta có: 3x + 2 = -3 ⇒ x = -5/3 ∉ Z (loại)

3x + 2 = -1 ⇒ x = - 1

3x + 2 = 1 ⇒ x = -1/3 ∉ Z (loại)

3x + 2 = 3 ⇒ x = 1/3 ∉ Z (loại)

x = -1 khác -3/2

Vậy với x = - 1 thì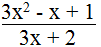có giá trị nguyên.

►► CLICK NGAY vào nút TẢI VỀ dưới đây để download Giải sách bài tập Toán lớp 8 tập 1 trang 36, 37, 38 file word, pdf hoàn toàn miễn phí.