Soạn Toán 8 Bài 2: Phương trình bậc nhất một ẩn và cách giải

Để quá trình tiếp thu kiến thức mới trở nên dễ dàng và đạt hiệu quả nhất, trước khi bắt đầu bài học mới các em cần có sự chuẩn bị nhất định qua việc tổng hợp nội dung kiến thức lý thuyết trọng tâm, sử dụng những kiến thức hiện có thử áp dụng giải các bài toán, trả lời câu hỏi liên quan. Dưới đây chúng tôi đã soạn sẵn Lời giải Toán 8 Bài 2: Phương trình bậc nhất một ẩn và cách giải đầy đủ nhất, giúp các em tiết kiệm thời gian. Nội dung chi tiết được chia sẻ dưới đây.

Bài 2: Phương trình bậc nhất một ẩn và cách giải

Câu hỏi ứng dụng

Câu hỏi 1 trang 8:

Giải các phương trình:

a) x – 4 = 0;

b) 3/4 + x = 0;

c) 0,5 – x = 0.

Hướng dẫn giải chi tiết:

a) x – 4 = 0

⇔ x = 0 + 4

⇔ x = 4

Vậy phương trình có một nghiệm duy nhất x = 4

b)3/4 + x = 0

⇔ x = 0-3/4

⇔ x = -3/4

Vậy phương trình có một nghiệm duy nhất x=-3/4

c) 0,5 – x = 0

⇔ x = 0,5-0

⇔ x = 0,5

Vậy phương trình có một nghiệm duy nhất x = 0,5

Câu hỏi 2 trang 8:

Giải các phương trình:

a) x/2 = -1;

b) 0,1x = 1,5;

c) -2,5x = 10.

Hướng dẫn giải chi tiết:

a) x/2 = -1

⇔ x = (-1).2

⇔ x = -2

Vậy phương trình có một nghiệm duy nhất x = -2

b) 0,1x = 1,5

⇔ x = 1,5/0,1

⇔ x = 15

Vậy phương trình có một nghiệm duy nhất x = 15

c) -2,5x = 10

⇔ x = 10/(-2,5)

⇔ x = -4

Vậy phương trình có một nghiệm duy nhất x = - 4

Câu hỏi 2 trang 9:

Giải phương trình: -0,5x + 2,4 = 0.

Hướng dẫn giải chi tiết:

- 0,5x + 2,4 = 0

⇔ -0,5x = -2,4

⇔ x = (-2,4)/(-0.5)

⇔ x = 4,8

Vậy phương trình có một nghiệm duy nhất x = 4,8

Bài tập ứng dụng

Bài 6 (trang 9 SGK Toán 8 tập 2):

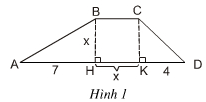
Tính diện tích S của hình thang ABCD theo x bằng hai cách:

1) Tính theo công thức: S = BH x (BC + DA) : 2

2) S = S_ABH + S_BCKH + S_CKD

Sau đó, sử dụng giả thiết S = 20 để thu được hai phương trình tương đương với nhau. Trong hai phương trình ấy, có phương trình nào là phương trình bậc nhất không?

Hướng dẫn giải chi tiết:

1) Công thức: S = BH x (BC + DA) : 2

+ Có BH ⊥ HK, CK ⊥ HK (giả thiết)

Mà BC // HK (vì ABCD là hình thang)

Do đó: BH ⊥ BC, CK ⊥ BC

Tứ giác BCKH có bốn góc vuông nên BCKH là hình chữ nhật.

Mặt khác: BH = HK = x (giả thiết) nên BCKH là hình vuông.

⇒ BH = BC = CK = KH = x

+ AD = AH + HK + KD = 7 + x + 4 = 11 + x.

Vậy S = BH x (BC + DA) : 2 = x.(x + 11 + x) : 2 = x.(2x + 11) : 2 = (11x + 2x²) / 2

2) S = S_ABH + S_BCKH + S_CKD

+ ABH là tam giác vuông tại H

⇒ S_BAH = 1/2.BH.AH = 1/2.7.x = 7x/2.

+ BCKH là hình chữ nhật

⇒ S_BCKH = x.x = x².

+ CKD là tam giác vuông tại K

⇒ S_CKD = 1/2.CK.KD = 1/2.4.x = 2x.

Do đó: S = S_ABH + S_BCKH + S_CKD = 7x/2 + x² + 2x = x² + 11x/2.

- Với S = 20 ta có phương trình:

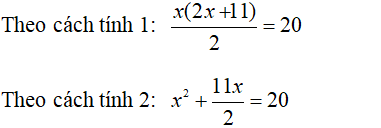
Hai phương trình trên tương đương với nhau. Và cả hai phương trình trên đều không phải là phương trình bậc nhất.

Kiến thức áp dụng

Phương trình bậc nhất là phương trình có dạng ax + b = 0, a ≠ 0.

Bài 7 (trang 10 SGK Toán 8 tập 2):

Hãy chỉ ra các phương trình bậc nhất trong các phương trình sau:

a) 1 + x = 0

b) x + x² = 0

c) 1 – 2t = 0

d) 3y = 0

e) 0x – 3 = 0.

Hướng dẫn giải chi tiết:

Phương trình dạng ax+ b= 0, với a, b là hai số đã cho và a ≠ 0 , được gọi là phương trình bậc nhất một ẩn.

+ Phương trình 1 + x = 0 là phương trình bậc nhất với a = 1 ; b = 1.

+ Phương trình x + x² = 0 không phải phương trình bậc nhất vì có chứa x² bậc hai.

+ Phương trình 1 – 2t = 0 là phương trình bậc nhất ẩn t với a = -2 và b = 1.

+ Phương trình 3y = 0 là phương trình bậc nhất ẩn y với a = 3 và b = 0.

+ Phương trình 0x – 3 = 0 không phải phương trình bậc nhất vì hệ số bậc nhất a = 0.

Kiến thức áp dụng

Phương trình bậc nhất là phương trình có dạng ax + b = 0 với a ≠ 0.

Bài 8 (trang 10 SGK Toán 8 tập 2):

Giải các phương trình:

a) 4x – 20 = 0

b) 2x + x + 12 = 0

c) x – 5 = 3 – x

d) 7 – 3x = 9 – x

Hướng dẫn giải chi tiết:

a) 4x – 20 = 0

⇔ 4x = 20

⇔ x = 20 : 4

⇔ x = 5

Vậy phương trình có nghiệm duy nhất x = 5.

b) 2x + x + 12 = 0

⇔ 3x + 12 = 0

⇔ 3x = -12

⇔ x = -12 : 3

⇔ x = -4

Vậy phương trình đã cho có nghiệm duy nhất x = -4

c) x – 5 = 3 – x

⇔ x + x = 5 + 3

⇔ 2x = 8

⇔ x = 8 : 2

⇔ x = 4

Vậy phương trình có nghiệm duy nhất x = 4

d) 7 – 3x = 9 – x

⇔ 7 – 9 = 3x – x

⇔ -2 = 2x

⇔ -2 : 2 = x

⇔ -1 = x

⇔ x = -1

Vậy phương trình có nghiệm duy nhất x = -1.

Kiến thức áp dụng

Để giải phương trình bậc nhất một ẩn ta sử dụng hai quy tắc sau:

+ Chuyển vế một hạng từ từ vế này sang vế khác và đổi dấu hạng tử đó.

+ Nhân hoặc chia cả hai vế với cùng một số khác 0.

Bài 9 (trang 10 SGK Toán 8 tập 2):

Giải các phương trình sau, viết số gần đúng của mỗi nghiệm ở dạng số thập phân bằng cách làm tròn đến hàng phần trăm.

a) 3x – 11 = 0

b) 12 + 7x = 0

c) 10 – 4x = 2x – 3

Hướng dẫn giải chi tiết:

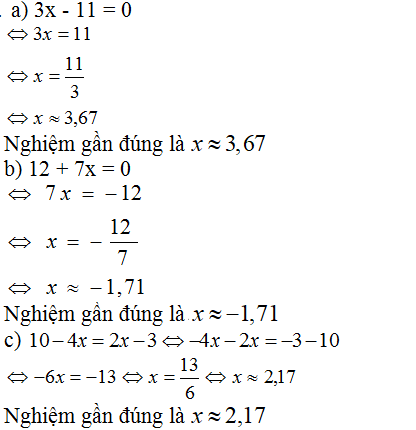
Kiến thức áp dụng

Để giải phương trình bậc nhất một ẩn ta sử dụng hai quy tắc sau:

+ Chuyển vế một hạng từ từ vế này sang vế khác và đổi dấu hạng tử đó.

+ Nhân hoặc chia cả hai vế với cùng một số khác 0.

Lý thuyết trọng tâm

Định nghĩa về phương trình bậc nhất một ẩn

Phương trình có dạng ax + b = 0, với a và b là hai số đã cho và a ≠ 0, được gọi là phương trình bậc nhất một ẩn.

Ví dụ:

Phương trình 2x - 3 = 0 là phương trình bậc nhất ẩn x.

Phương trình y - 4 = 2 là phương trình bậc nhất ẩn y.

Hai quy tắc biến đổi phương trình

a) Quy tắc chuyển vế

Trong một phương trình ta có thể chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó.

Ví dụ: Giải phương trình x + 3 = 0

Hướng dẫn:

Ta có x + 3 = 0 ⇔ x = - 3. (chuyển hạng tử + 3 từ vế trái sang vế phải và đổi thành - 3 ta được x = - 3 )

b) Quy tắc nhân với một số

Trong một phương trình, ta có thể nhân cả hai vế với cùng một số khác 0.

Ví dụ: Giải phương trình x/2 = - 2.

Hướng dẫn:

Ta có x/2 = - 2 ⇔ 2.x/2 = - 2.2 ⇔ x = - 4. (nhân cả hai vế với số 2 ta được x = - 4 )

Cách giải phương trình bậc nhất một ẩn

Phương trình có dạng ax + b = 0, với a và b là hai số đã cho và a ≠ 0, được gọi là phương trình bậc nhất một ẩn.

Cách giải:

    Bước 1: Chuyển vế ax = - b.

    Bước 2: Chia hai vế cho a ta được: x = - b/a.

   Bước 3: Kết luận nghiệm: S = { - b/a }.

Ta có thể trình bày ngắn gọn như sau:

ax + b = 0 ⇔ ax = - b ⇔ x = - b/a.

Vậy phương trình có tập nghiệm là S = { - b/a }.

File tải hướng dẫn soạn Bài 2: Phương trình bậc nhất một ẩn và cách giải:

Hy vọng tài liệu sẽ hữu ích cho các em học sinh và quý thầy cô giáo tham khảo và đối chiếu đáp án chính xác.

►Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích hỗ trợ ôn luyện thi môn toán như đề kiểm tra học kì, 1 tiết, 15 phút trên lớp, hướng dẫn giải sách giáo khoa, sách bài tập được cập nhật liên tục tại chuyên trang của chúng tôi.