Giải Toán lớp 8 trang 38, 39, 40 SGK tập 2 chính xác nhất

Hướng dẫn giải sách giáo khoa Toán lớp 8 trang 38, 39, 40 tập 2 bài: Liên hệ giữa thứ tự và phép nhân đầy đủ, chi tiết nhất. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài học sắp tới được tốt nhất.

Trả lời câu hỏi Sách giáo khoa Toán 8 Tập 2 trang 38

a) Nhân cả hai vế của bất đẳng thức -2 < 3 với 5091 thì được bất đẳng thức nào?

b) Dự đoán kết quả: Nhân cả hai vế của bất đẳng thức -2 < 3 với số c dương thì ta được bất đẳng thức nào?

Lời giải

a) - 2. 5091 = - 10 182 và 3. 5091 = 15 273

⇒ - 10 182 < 15 273

b) Nhân cả hai vế của bất đẳng thức -2 < 3 với số c dương thì ta được bất đẳng thức: -2c < 3c

Trả lời câu hỏi Toán lớp 8 SGK Tập 2 trang 38

Đặt dấu thích hợp (<, >) vào ô vuông:

a) (-15,2) . 3,5 .....(-15,08) . 3,5;

b) 4,15 . 2,2 ..... (-5,3) . 2,2.

Lời giải

a) (-15,2) . 3,5 < (-15,08) . 3,5

b) 4,15 . 2,2 > (-5,3) . 2,2

Trả lời câu hỏi Toán 8 Tập 2 SGK trang 38

a) Nhân cả hai vế của bất đẳng thức -2 < 3 với -345 thì được bất đẳng thức nào?

b) Dự đoán kết quả: Nhân cả hai vế của bất đẳng thức -2 < 3 với số c âm thì ta được bất đẳng thức nào?

Lời giải

a) – 2 . (- 345) = 690; 3 . 345 = - 1035

⇒ 690 > - 1035

b) Nhân cả hai vế của bất đẳng thức -2 < 3 với số c âm thì ta được bất đẳng thức: -2c > 3c

Trả lời câu hỏi trang 39 SGK Toán 8 Tập 2 

Cho -4a > -4b, hãy so sánh a và b.

Lời giải

a < b

Trả lời câu hỏi trang 39 SGK Toán 8 Tập 2

Khi chia cả hai vế của bất đẳng thức cho cùng một số khác không thì sao?

Lời giải

- Khi chia cả hai vế của bất đẳng thức cho cùng một số dương: Bất đằng thức không đổi dấu

- Khi chia cả hai vế của bất đẳng thức cho cùng một số âm: bất đằng thức đổi dấu

Giải bài 5 trang 39 SGK Toán tập 2 lớp 8

Mỗi khẳng định sau đúng hay sai? Vì sao?

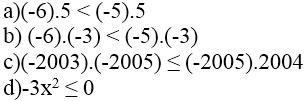
Lời giải:

(Áp dụng quy tắc: Khi nhân hai vế của bất đẳng thức với một số dương thì được bất đẳng thức cùng chiều, khi nhân với số âm thì được bất đẳng thức ngược chiều với bất đẳng thức đã cho.)

a) Vì -6 < -5 (*) nên khẳng định (-6).5 < (-5).5 đúng vì nhân hai vế của (*) với một số dương là 5.

b) Khẳng định (-6).(-3) < (-5).(-3) sai vì nhân hai vế của (*) với một số âm là (-3).

c) Vì -2003 ≤ 2004 (**) nên khẳng định (-2003).(-2005) ≤ (-2005).2004 sai vì nhân hai vế của (**) với một số âm là (-2005).

d) Vì x² ≥ 0 với mọi x ∈ R nên -x² ≤ 0 (***)

Do đó khẳng định -3x² ≤ 0 đúng vì nhân hai vế của (***) với một số dương là 3.

(Lưu ý: bạn có thể trình bày ngắn gọn hơn nếu bạn đã hiểu bài, ví dụ:

Vì -6 < -5 và 5 > 0 nên khẳng định đúng.)

(Cách khác: sử dụng máy tính để tính trực tiếp, rồi sau đó so sánh và đưa ra kết luận.)

Giải bài 6 SGK Toán lớp 8 trang 39 tập 2

Cho a < b, hãy so sánh:

2a và 2b; 2a và a + b; -a + b; -a và -b.

Lời giải:

(Áp dụng quy tắc: khi nhân hai vế của bất đẳng thức với một số dương thì được bất đẳng thức cùng chiều, khi nhân với số âm thì được bất đẳng thức ngược chiều với bất đẳng thức đã cho.

Và quy tắc cộng cùng một số vào hai vế của một bất đẳng thức.)

Vì a < b (*):

- mà 2 > 0 nên 2a < 2b (nhân hai vế (*) với số dương)

- nên 2a < a + b (cộng hai vế (*) với a)

- mà -1 < 0 nên -a > -b (nhân hai vế (*) với số âm)

Giải bài 7 trang 40 tập 2 SGK Toán lớp 8

Số a là số âm hay dương nếu:

12a < 15 a? 4a < 3a? -3a > -5a?

Lời giải:

(Áp dụng quy tắc: Khi nhân hai vế của bất đẳng thức với một số dương thì được bất đẳng thức cùng chiều, khi nhân với số âm thì được bất đẳng thức ngược chiều với bất đẳng thức đã cho.)

a) Ta có: 12 < 15 (*). Để có bất đẳng thức cùng chiều là 12a < 15a ta phải nhân cả hai vế của (*) với số dương. Vậy a là số dương.

b) Ta có: 4 > 3 (**). Để có bất đẳng thức trái chiều là 4a < 3a ta phải nhân cả hai vế của (**) với số âm. Vậy a là số âm.

c) Ta có: -3 > -5 (***). Để có bất đẳng thức cùng chiều là -3a > -5a ta phải nhân cả hai vế của (*) với số dương. Vậy a là số dương.

Giải bài 8 SGK Toán lớp 8 tập 2 trang 40

Cho a < b, chứng tỏ:

a) 2a - 3 < 2b - 3; b) 2a - 3 < 2b + 5.

Lời giải:

(Áp dụng quy tắc: Khi nhân hai vế của bất đẳng thức với một số dương thì được bất đẳng thức cùng chiều, khi nhân với số âm thì được bất đẳng thức ngược chiều với bất đẳng thức đã cho.

Và quy tắc cộng cùng một số vào hai vế của một bất đẳng thức.)

a) Ta có: a < b mà 2 > 0

nên 2a - 3 < 2b - 3 (cộng vào cả hai vế với - 3) (đpcm).

b) Ta có: -3 < 5

=> 2b - 3 < 2b + 5 (cộng vào hai vế với 2b)

mà 2a - 3 < 2b - 3 (chứng minh ở câu a))

Vậy: 2a - 3 < 2b + 5 (Tính chất bắc cầu)

Giải bài 9 trang 40 SGK Toán lớp 8 tập 2

Cho tam giác ABC. Các khẳng định sau đúng hay sai?

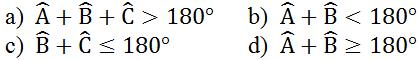
Lời giải:

Theo định lí tổng ba góc trong tam giác thì trong

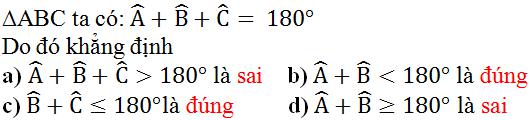
Giải bài 10 SGK Toán trang 40 lớp 8 tập 2 

a) So sánh (-2).3 và -4,5.

b) Từ kết quả câu a) hãy suy ra các bất đẳng thức sau:

(-2).30 < -45; (-2).3 + 4,5 < 0

Lời giải:

a) Ta có: -2 < -1,5 và 3 > 0

=> (-2).3 < (-1,5).3 (nhân hai vế với 3)

=> (-2).3 < -4,5 (*)

b) Từ (*) ta nhân cả hai vế của bất đẳng thức với 10 > 0 thì được:

(-2).30 < -45

Từ (*) ta cộng cả hai vế với 4,5 thì được:

=> (-2).3 + 4,5 < -4,5 + 4,5

=> (-2).3 + 4,5 < 0

Giải bài 11 lớp 8 SGK Toán tập 2 trang 40

Cho a < b, chứng minh:

a) 3a + 1 < 3b + 1; b) -2a – 5 > -2b - 5

Lời giải:

a) Vì a < b

=> 3a < 3b (nhân hai vế với 3 > 0)

=> 3a + 1 < 3b + 1 (cộng hai vế với 1) (đpcm)

b) Vì a < b

=> -2a > -2b (nhân hai vế với -2 < 0)

=> -2a – 5 > -2b – 5 (cộng hai vế với -5) (đpcm)

Giải bài 12 trang 40 SGK Toán tập 2 lớp 8

 Chứng minh:

a) 4.(-2) + 14 < 4.(-1) + 14; b) (-3).2 + 5 < (-3).(-5) + 5

Lời giải:

a) Ta có: -2 < -1

=> 4.(-2) < 4.(-1) (nhân hai vế với 4)

=> 4.(-2) + 14 < 4.(-1) + 14 (cộng hai vế với 14) (đpcm)

b) Ta có: 2 > -5

=> (-3).2 < (-3).(-5) (nhân hai vế với -3)

=> (-3).2 + 5 < (-3).(-5) + 5 (cộng hai vế với 5) (đpcm)

Giải bài 13 SGK Toán lớp 8 trang 40 tập 2

a) a + 5 < b + 5;        b) – 3a > -3b

c) 5a – 6 ≥ 5b – 6;     d) -2a + 3 ≤ - 2b + 3

Lời giải:

a) Từ a + 5 < b + 5

⇒ a + 5 + (-5) < b + 5 + (-5) (cộng hai vế với -5)

⇒ a < b

b) -3.a > -3.b

⇒ a < b (Nhân cả hai vế cho 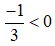 < 0, BĐT đổi chiều).

c) 5a – 6 ≥ 5b – 6

⇒ 5a – 6 + 6 ≥ 5b – 6 + 6 (Cộng hai vế với 6)

⇒ 5a ≥ 5b

⇒ a ≥ b (Nhân cả hai vế cho 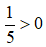 > 0, BĐT không đổi chiều).

d) -2a + 3 ≤ - 2b + 3

⇒ -2a + 3 – 3 ≤ - 2b + 3 – 3 (Cộng cả hai vế với -3)

⇒ -2a ≤ - 2b

⇒ a ≥ b (Nhân cả hai vế cho 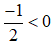 < 0, BĐT đổi chiều).

Giải bài 14 trang 40 tập 2 SGK Toán lớp 8

Cho a < b, hãy so sánh:

2a + 1 với 2b + 1; 2a + 1 với 2b + 3

Lời giải:

a) Từ a < b => 2a < 2b (nhân hai vế với 2 > 0)

=> 2a + 1 < 2b + 1 (*) (cộng hai vế với 1)

b) Ta có 2b + 1 < 2b + 3 với mọi số thực b.

Kết hợp với (*) ta suy ra:

2a + 1 < 2b + 3 (tính chất bắc cầu)

►► CLICK NGAY vào nút TẢI VỀ dưới đây để giải toán lớp 8 SGK trang 38, 39, 40 tập 2 file word, pdf hoàn toàn miễn phí.