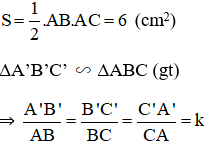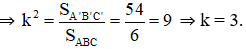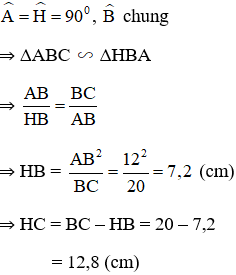Giải bài tập Toán hình lớp 8 trang 81, 84, 85 SGK tập 2 chi tiết nhất

Hướng dẫn giải sách giáo khoa Toán lớp 8 trang 81, 84, 85 tập 2 bài 8: Các trường hợp đồng dạng của tam giác vuông đầy đủ, chi tiết nhất. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài học sắp tới được tốt nhất.

Trả lời câu hỏi SGK Toán hình lớp 8 trang 81 tập 2

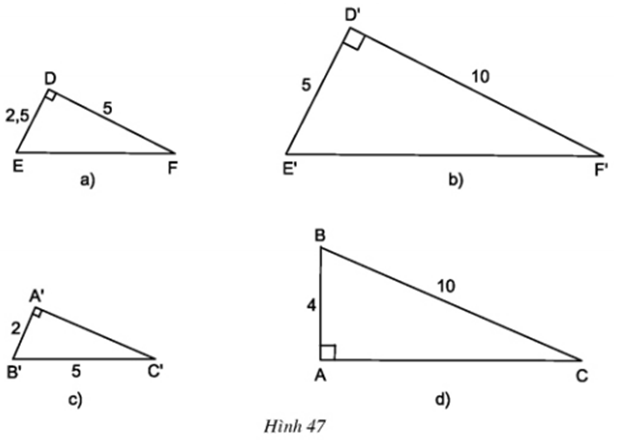
Hãy chỉ ra các cặp tam giác đồng dạng trong hình 47.

Lời giải

Hai tam giác vuông ΔDEF và ΔD’E’F’ có

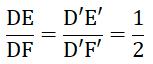
⇒ ΔABD ∼ ΔACB (hai cạnh góc vuông)

Áp dụng định lí Py – ta – go:

A'C'² = B'C'² - A'B'² = 5² -2² = 21 ⇒ A'C' = √21

AC² = BC² - AB² = 10² - 4² = 84 ⇒ AC = √84 = 2√21

Hai tam giác vuông ΔABC và ΔA’B’C’ có

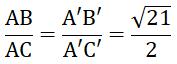
⇒ ΔABC ∼ ΔA’B’C’ (hai cạnh góc vuông)

Giải bài 46 trang 84 SGK Toán hình tập 2 lớp 8

Trên hình 50 hãy chỉ ra các tam giác đồng dạng. Viết các tam giác này theo thứ tự các đỉnh tương ứng và giải thích vì sao chúng đồng dạng?

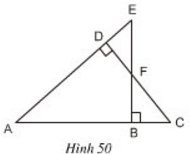
Lời giải:

Giải bài 47 SGK Toán hình lớp 8 trang 84 tập 2

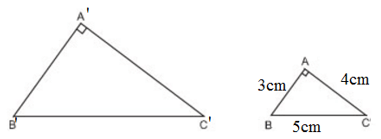
Tam giác ABC có độ dài các cạnh là 3cm, 4cm, 5cm. Tam giác A'B'C' đồng dạng với tam giác ABC và có diện tích là 54cm². Tính độ dài các cạnh của tam giác A'B'C'.

Lời giải:

Xét ΔABC có: AB² + AC² = 3² + 4² = 25 = 5² = BC²

⇒ ΔABC vuông tại A (Định lý Pytago đảo)

⇒ Diện tích tam giác ABC bằng:

(với k là tỉ số đồng dạng).

Lại có tỉ số diện tích bằng bình phương tỉ số đồng dạng

⇒ A’B’ = 3.AB = 3.3 = 9 (cm)

B’C’ = 3.BC = 3.5 = 15 (cm)

C’A’ = 3.CA = 3.4 = 12 (cm)

Vậy độ dài ba cạnh của tam giác lần lượt là 9cm, 12cm, 15cm.

Giải bài 48 trang 84 tập 2 SGK Toán hình lớp 8

Bóng của cột điện trên mặt đất có độ dài là 4,5m. Cùng thời điểm đó, một thanh sắt cao 2,1m cắm vuông góc với mặt đất có bóng dài 0,6m. Tính chiều cao của cột điện.

Lời giải:

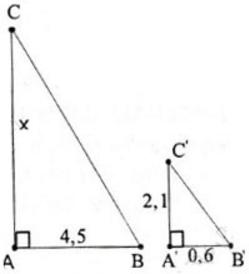
Giả sử cột điện là AC, có bóng trên mặt đất là AB.

Thanh sắt là A'C', có bóng trên mặt đất là A'B'.

Vì cột điện và thanh sắt đều vuông góc với mặt đất nên hai tam giác ABC và A'B'C' đều là tam giác vuông.

Vì cùng một thời điểm tia sáng chiếu nên ta suy ra góc ACB = góc A'C'B'

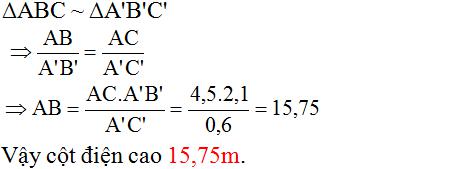
Giải bài 49 SGK Toán hình lớp 8 tập 2 trang 84

Ở hình 51, tam giác ABC vuông ở A và có đường cao AH.

a) Trong hình vẽ có bao nhiêu cặp tam giác đồng dạng với nhau? (Hãy chỉ rõ từng cặp tam giác đồng dạng và viết theo các đỉnh tương ứng).

b) Cho biết AB = 12,45cm, AC = 20,50cm. Tính độ dài các đoạn thẳng BC, AH, BH và CH.

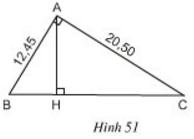
Lời giải:

Giải bài 50 trang 84 SGK Toán hình lớp 8 tập 2

Bóng của một ống khói nhà máy trên mặt đất có độ dài là 36,9m. Cùng thời điểm đó, một thanh sắt cao 2,1m cắm vuông góc với mặt đất có bóng dài 1,62m. Tính chiều cao của ống khói (h.52).

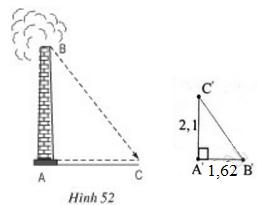
Lời giải:

Tương tự bài 48 trang 84 SGK Toán hình 8 tập 2

Giả sử thanh sắt là A'C', có bóng là A'B'.

Vì ống khói và thanh sắt đều vuông góc với mặt đất nên hai tam giác ABC và A'B'C' đều là tam giác vuông.

Vì cùng một thời điểm tia sáng chiếu nên ta suy ra góc ACB = góc A'C'B'

=> ΔABC ∼ ΔA'B'C' nên

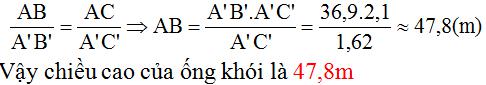
Giải bài 51 SGK Toán hình trang 84 lớp 8 tập 2 

Chân đường cao AH của tam giác vuông ABC chia cạnh huyền BC thành hai đoạn thẳng có độ dài 25cm và 36cm. Tính chu vi và diện tích của tam giác vuông đó (h.53).

Hướng dẫn: Trước tiên tìm cách tính AH từ các tam giác vuông đồng dạng, sau đó tính các cạnh của tam giác ABC.

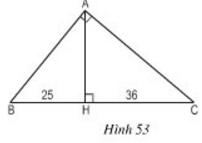
Lời giải:

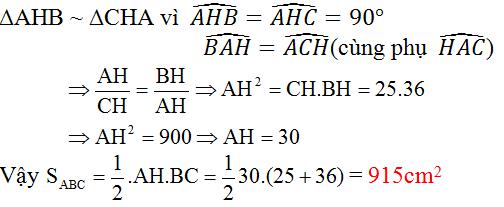
Áp dụng Py-ta-go cho 2 tam giác vuông ABH và ACH:

*AB² = BH² + AH²

⇒AB² = 25² + 30²

⇒AB² = 1525

⇒AB = 39,05

*AC² = CH² + AH²

⇒AC² = 36² + 30²

⇒AC² = 2196

⇒AC = 46,86

Chu vi tam giác ABC là: P= AB+AC+BC=39,05+46,86+61=146.91(cm)

Giải bài 52 lớp 8 SGK Toán hình tập 2 trang 85

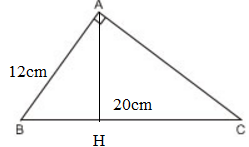
Cho một tam giác vuông, trong đó cạnh huyền dài 20cm và một cạnh góc vuông dài 12cm. Tính độ dài hình chiếu cạnh góc vuông kia trên cạnh huyền.

Lời giải:

 

ΔABC vuông tại A có đường cao AH, BC = 20cm, AB = 12cm. Ta tính HC.

ΔABC và ΔHBA có:

►► CLICK NGAY vào nút TẢI VỀ dưới đây để giải Toán lớp 8 Sách giáo khoa trang trang 81, 84, 85 tập 2 file word, pdf hoàn toàn miễn phí.