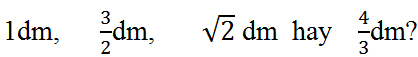Giải Toán hình học lớp 8 trang 107, 108, 109 SGK tập 1: Hình vuông

Hướng dẫn giải sách giáo khoa Toán lớp 8 trang 107, 108, 109 tập 1: Hình vuông đầy đủ, chi tiết nhất. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài học sắp tới được tốt nhất.

Trả lời câu hỏi Toán 8 trang 107 SGK tập 1

Đường chéo của hình vuông có những tính chất gì ?

Lời giải

Hình vuông có tất cả các hình chữ nhật và hình thoi

⇒ Hai đường chéo của hình vuông có tính chất:

Hai đường chéo bằng nhau

Hai đường chéo cắt nhau tại trung điểm mỗi đường

Hai đường chéo vuông góc với nhau

Trả lời câu hỏi SGK Toán lớp 8 tập 1 trang 108

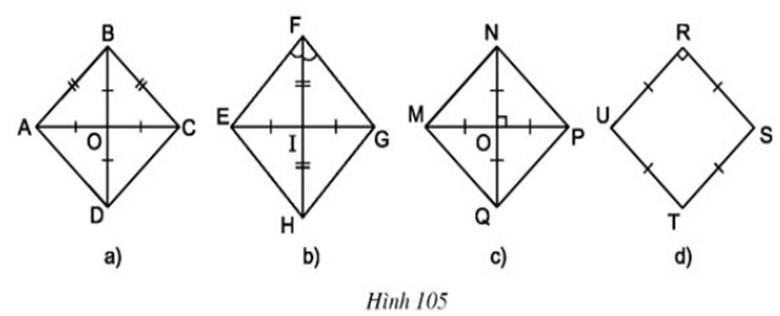
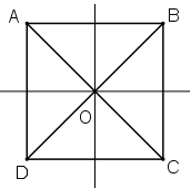
Tìm các hình vuông trên hình 105.

Lời giải

- ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường ⇒ ABCD là hình bình hành

Hình bình hành ABCD có hai đường chéo bằng nhau ⇒ ABCD là hình chữ nhật

Hình chữ nhật ABCD có AB = BC ⇒ ABCD là hình vuông

- MNPQ có hai đường chéo cắt nhau tại trung điểm mỗi đường ⇒ MNPQ là hình bình hành

Hình bình hành MNPQ có hai đường chéo bằng nhau ⇒ MNPQ là hình chữ nhật

Hình chữ nhật MNPQ có MP ⊥ NQ tại O ⇒ MNPQ là hình vuông

- RSTU có 4 cạnh bằng nhau ⇒ RSTU là hình thoi

Hình thoi RSTU có một góc vuông ⇒ RSTU là hình vuông

Giải bài 79 trang 108 SGK Toán tập 1 lớp 8

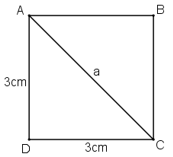
a) Một hình vuông có cạnh bằng 3cm. Đường chéo của hình vuông đó bằng: 6cm,    √18 cm,     5cm hay 4cm?

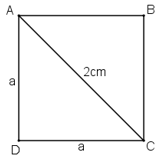
b) Đường chéo của một hình vuông bằng 2dm. Cạnh của hình vuông đó bằng:

Lời giải:

a)

Gọi đường chéo của hình vuông có độ dài là a.

Áp dụng định lí Pi-ta-go ta có:

a² = 3² + 3² = 18 suy ra a = √18 = 3√2

Vậy đường chéo của hình vuông đó bằng 3√2 (cm)

b)

Gọi cạnh của hình vuông là a.

Áp dụng định lí Pi-ta-go ta có:

a² + a² = 2² ⇒ 2a² = 4

⇒ a² = 2 ⇒ a = √2

Vậy cạnh của hình vuông đó bằng √2 (dm).

Giải bài 80 SGK Toán lớp 8 trang 108 tập 1

Hãy chỉ rõ tâm đối xứng của hình vuông, các trục đối xứng của hình vuông.

Lời giải:

+ Hình vuông cũng là hình bình hành nên nhận O là giao điểm của hai đường chéo là tâm đối xứng.

+ Hình vuông cũng là hình thoi nên nhận hai đường chéo AC và BD là các trục đối xứng.

+ Hình vuông cũng là hình thang cân nên nhận đường thẳng nối trung điểm các cặp cạnh đối diện là trục đối xứng.

Vậy hình vuông có 1 tâm đối xứng và 4 trục đối xứng như trên.

Giải bài 81 trang 108 tập 1 SGK Toán lớp 8

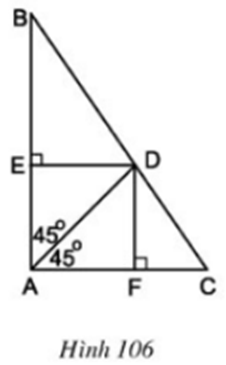
Cho hình 106. Tứ giác AEDF là hình gì? Vì sao?

Lời giải:

Cách 1:

Tứ giác AEDF có EA // DF (cùng vuông góc AF)

DE // FA (cùng vuông góc AE)

⇒ AEDF là hình bình hành (theo định nghĩa)

Hình bình hành AEDF có đường chéo AD là phân giác của góc A

⇒AEDF là hình thoi.

Hình thoi AEDF có Â = 90º

⇒ AEDF là hình vuông.

Giải bài 82 SGK Toán lớp 8 tập 1 trang 108

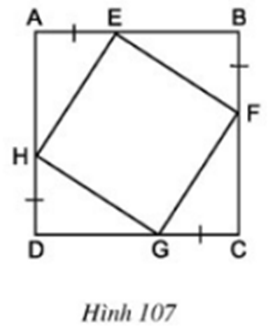
Cho hình 107, trong đó ABCD là hình vuông. Chứng minh rằng tứ giác EFGH là hình vuông.

Lời giải:

* Do ABCD là hình vuông nên AB = BC = CD = DA.

Theo giả thiết ta có: AE = BF = CG = DH nên ta có:

AB – AE = BC – BF = CD – CG = DA – DH

⇔ BE = CF= DG = HA

* Xét các tam giác vuông AEH, BFE, CGF, DHG có:

AE= BF = CG = DH (giả thiết)

HA= BE = CF = DG (chứng minh trên)

⇒ ΔAEH = ΔBFE = ΔCGF = ΔDHG ( c.g.c)

Suy ra: HE = EF = FG = GH (các cạnh tương ứng)

* Tứ giác EFGH là hình thoi có 1 góc bằng 90^o nên EFGH là hình vuông.

Giải bài 83 trang 109 SGK Toán lớp 8 tập 1

Các câu sau đúng hay sai?

a) Tứ giác có hai đường chéo vuông góc với nhau là hình thoi.

b) Tứ giác có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường là hình thoi.

c) Hình thoi là tứ giác có tất cả các cạnh bằng nhau.

d) Hình chữ nhật có hai đường chéo bằng nhau là hình vuông.

e) Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

Lời giải:

- Các câu a và d sai.

- Các câu b, c, e đúng.

Giải bài 84 SGK Toán trang 109 lớp 8 tập 1 

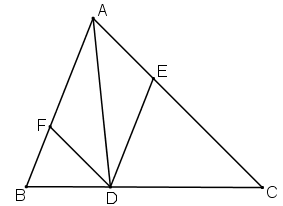
Cho tam giác ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự ở E và F.

a) Tứ giác AEDF là hình gì? Vì sao?

b) Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình thoi?

c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì? Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình vuông?

Lời giải:

a) Tứ giác AEDF là hình bình hành.

Vì có DE // AF, DF // AE (gt) (theo định nghĩa)

b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.

c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).

d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).

Giải bài 85 lớp 8 SGK Toán tập 1 trang 109

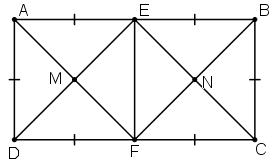
Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung diểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.

a) Tứ giác ADFE là hình gì? Vì sao?

b) Tứ giác EMFN là hình gì? Vì sao?

Lời giải:

a) E, F là trung điểm AB, CD ⇒ AE = EB = AB/2, DF = FC = CD/2.

Ta có: AB = CD = 2AD = 2BC

⇒ AE = EB = BC = CF = FD = DA.

+ Tứ giác ADFE có AE // DF, AE = DF

⇒ ADFE là hình bình hành.

Hình bình hành ADFE có Â = 90º

⇒ ADFE là hình chữ nhật.

Hình chữ nhật ADFE là hình chữ nhật có AE= AD

⇒ ADFE là hình vuông.

b) Tứ giác DEBF có EB // DF, EB = DF nên là hình bình hành

Do đó DE // BF

Tương tự: AF // EC

Suy ra EMFN là hình bình hành

Theo câu a, ADFE là hình vuông nên ME = MF, ME ⊥ MF.

Hình bình hành EMFN có M̂ = 90º nên là hình chữ nhật.

Lại có ME = MF nên EMFN là hình vuông.

Giải bài 86 trang 109 SGK Toán tập 1 lớp 8

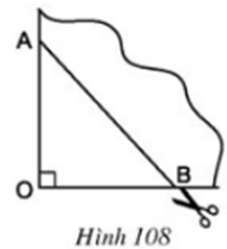
Đố.  Lấy một tờ giấy gấp làm tư rồi cắt chéo theo nhát cắt AB (h.108). Sau khi mở tờ giấy ra, ta được một tứ giác. Tứ giác nhận được là hình gì? Vì sao? Nếu ta có OA = OB thì tứ giác nhận được là hình gì?

Lời giải:

- Tứ giác nhận được theo nhát cắt của AB là hình thoi vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau.

- Nếu có thêm OA = OB thì hình thoi nhận được có hai đường chéo bằng nhau nên là hình vuông.

CLICK NGAY vào nút TẢI VỀ dưới đây để giải Toán lớp 8 Sách giáo khoa trang 107, 108, 109 tập 1 file word, pdf hoàn toàn miễn phí.