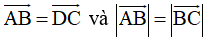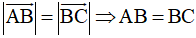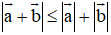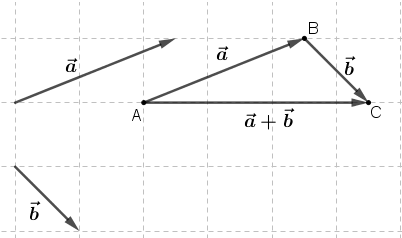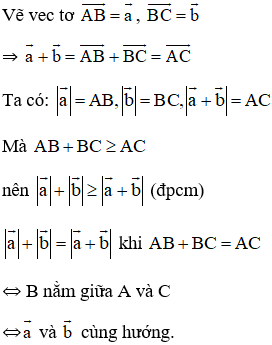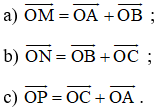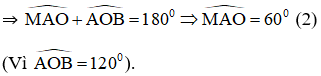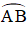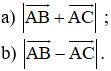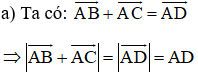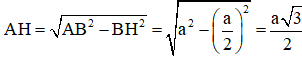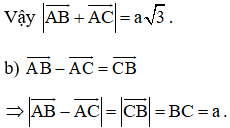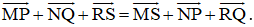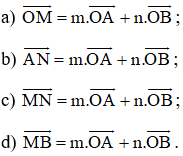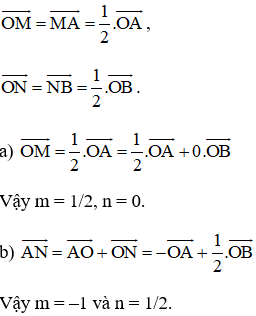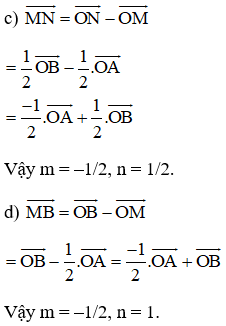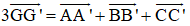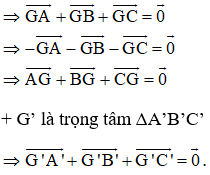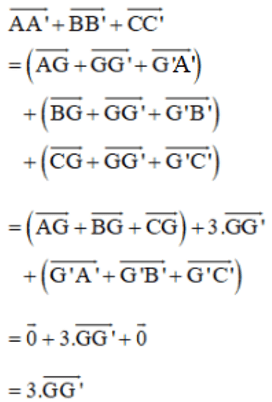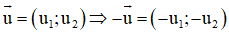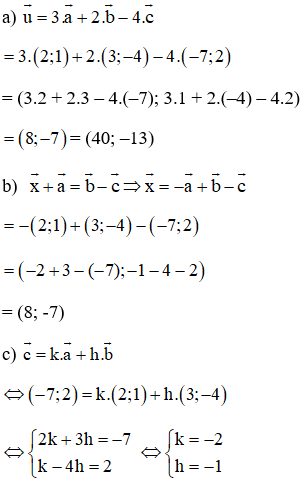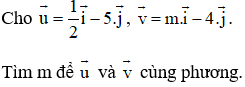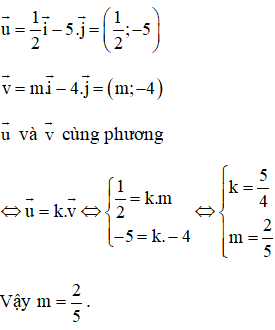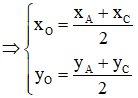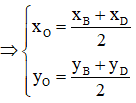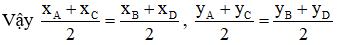Giải bài tập Toán hình 10 trang 27, 28 SGK tập 1: Ôn tập chương 1

Hướng dẫn giải Toán hình lớp 10 sách giáo khoa trang 27, 28 bài: Ôn tập chương 1 đầy đủ, chi tiết nhất. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị tốt nhất cho bài học sắp tới nhé.

Giải bài 1 SGK Toán hình lớp 10 tập 1 trang 27

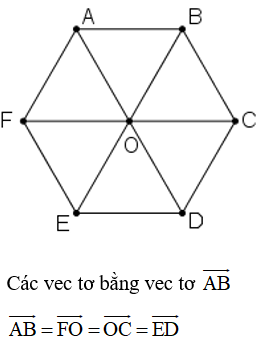
Cho lục giác đều ABCDEF tâm O. Hãy chỉ ra các vectơ bằng vectơ AB có điểm đầu và điểm cuối là O hoặc các đỉnh của lục giác.

Lời giải:

Giải bài 2 trang 27 SGK hình học Toán 10 tập 1

Cho hai vectơ a và b đều khác vectơ 0. Các khẳng định sau đúng hay sai?

a, Hai vecto cùng hướng thì cùng phương.

b, Hai vecto b→ và kb→ cùng phương.

c, Hai vecto a→ và (-2)a→ cùng hướng.

d) Hai vector ngược hướng với vector thứ ba khác vectơ 0→ thì cùng phương.

Lời giải:

a) Đúng

b) Đúng

c) Sai

d) Đúng

Giải Toán hình học SGK lớp 10 tập 1 bài 3 trang 27

Tứ giác ABCD là hình gì nếu 

Lời giải:

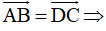
 tứ giác ABCD là hình bình hành

⇒ tứ giác ABCD là hình thoi.

(Hình bình hành có hai cạnh kề bằng nhau là hình thoi)

Giải SGK Toán hình lớp 10 tập 1 trang 27 bài 4

Chứng minh rằng 

Lời giải:

Giải bài 5 sách Toán hình 10 tập 1 trang 27

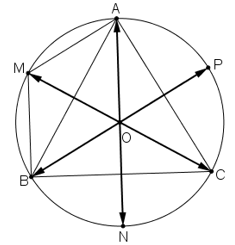
Cho tam giác đều ABC nội tiếp đường tròn tâm O. Hãy xác định các điểm M, N, P sao cho:

Lời giải:

a) 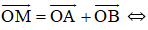 M là đỉnh còn lại của hình bình hành AOBM.

+ AOBM là hình bình hành ⇒ AM = OB

Mà OB = OA (= bán kính đường tròn) ⇒ AM = AO ⇒ ΔAMO cân tại A (1)

+ AOBM là hình bình hành ⇒ AM//BO

Từ (1) và (2) ⇒ ΔAMO đều ⇒ OM = OA ⇒ M nằm trên đường tròn ngoại tiếp ΔABC.

Mà 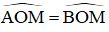 nên M là điểm chính giữa cung 

b) Chứng minh tương tự phần a) ta có: 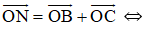 N là điểm c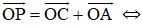hính giữa cung BC.

c)  P là điểm chính giữa cung CA.

Giải Toán SGK hình lớp 10 tập 1 trang 27 bài 6

Cho tam giác đều ABC có cạnh bằng a. Tính:

Lời giải:

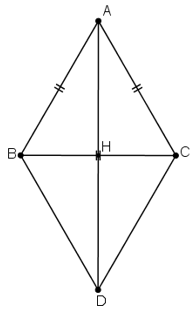
Vẽ hình bình hành ABDC, gọi H là giao điểm của AD và BC.

+ Hình bình hành ABDC có AB = AC ⇒ ABDC là hình thoi ⇒ AD ⊥ BC tại H.

+ H là trung điểm BC ⇒ BH = BC/2 = a/2.

+ ΔABH vuông tại H nên:

+ H là trung điểm AD ⇒ AD = 2. AH = a√3.

Giải Toán hình học lớp 10 tập 1 bài 7 trang 28

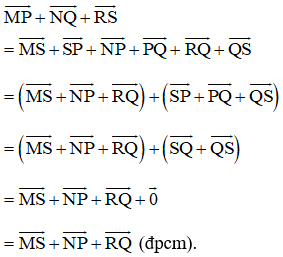
Cho sáu điểm M, N, P, Q, R, S bất kỳ. Chứng minh rằng:

Lời giải:

Áp dụng quy tắc ba điểm ta có:

Giải bài 8 trang 28 sách giáo khoa Toán hình lớp 10 tập 1

Cho tam giác OAB. Gọi M, N lần lượt là trung điểm của OA và OB. Tìm các số m, n sao cho:

Lời giải:

Giải bài 9 trang 28 SGK Toán hình học 10 tập 1

Chứng minh rằng nếu G và G' lần lượt là trọng tâm của các tam giác ABC và A'B'C' thì 

Lời giải:

+ G là trọng tâm ΔABC

Khi đó

Giải bài 10 SGK Toán hình lớp 10 trang 28 tập 1

Trong mặt phẳng tọa độ Oxy, các khẳng định sau đúng hay sai?

a, Hai vecto đối nhau thì chúng có hoành độ đối nhau.

b, Vecto a→ ≠ 0→ cùng phương với vecto i→ nếu a→ có hoành độ bằng 0.

c, Vecto a→ có hoành độ bằng 0 thì cùng phương với vecta j→

Lời giải:

a) Đúng.

Hai vec tơ đối nhau thì chúng có hoành độ đối nhau và tung độ đối nhau.

b) Sai.

Sửa lại: Vec tơ a→ cùng phương với vec tơ i→ nếu a→ có tung độ bằng 0.

c) Đúng.

Giải bài 11 SGK Toán hình lớp 10 tập 1 trang 28

Lời giải:

Giải SGK hình học Toán 10 tập 1 bài 12 trang 28

Lời giải:

Giải bài 13 SGK Toán hình lớp 10 tập 1 trang 28

Trong các khẳng định sau, khẳng định nào đúng?

a) Điểm A nằm trên trục hoành thì có hoành độ bằng 0.

b) P là trung điểm của đoạn thẳng AB khi và chỉ khi hoành độ của P bằng trung bình cộng các hoành độ của A và B.

c) Nếu tứ giác ABCD là hình bình hành thì trung bình cộng các tọa độ tương ứng của A và C bằng trung bình cộng các tọa độ tương ứng của B và D.

Lời giải:

a) Sai

Sửa lại: Điểm A nằm trên trục hoành thì có tung độ bằng 0.

b) Sai

Ví dụ: A(2; 6), B(–4; 0) có trung bình cộng các hoành độ bằng –1.

P(–1; 3) là trung điểm của AB

P(–1; 2) không phải trung điểm của AB

P(–1; 0) không phải trung điểm của AB.

c) Đúng

ABCD là hình bình hành nên giao điểm O của AC và BD đồng thời là trung điểm của AC và BD

O là trung điểm của AC 

O là trung điểm của BD 

CLICK NGAY vào nút TẢI VỀ dưới đây để giải toán lớp 10 SGK trang 27, 28 file word, pdf hoàn toàn miễn phí.