Giải toán lớp 10 trang 38, 39 SGK tập 1, chương 2: Hàm số

Hướng dẫn cách giải bài tập Sách giáo khoa Toán lớp 10 trang 38, 39, chương 2 bài Hàm số đầy đủ và chi tiết nhất dưới đây, giúp các bạn học sinh củng cố kiến thức đã được học và vận dụng để có thể giải các dạng toán với yêu cầu tương tự như vậy.

Giải bài tập Toán lớp 10 tập 1 Sách giáo khoa trang 38, 39

Xem ngay lời giải các bài tập 1, 2, 3, 4 sách giáo khoa Toán đại lớp 10 chi tiết như sau:

Giải bài 1 trang 38 SGK Toán lớp 10 tập 1

Tìm tập xác định các hàm số:

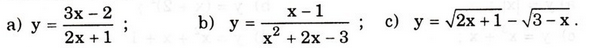
Hướng dẫn giải bài 1:

a) D = {x ∈ R / 2x + 1 ≠0 } hay D = R\{-1/2}

b) D = {x ∈ R / x² + 2x – 3 ≠0 } hay D = R\{1; -3}

c) D = {x ∈ R / √(2x + 1) và √(3 - x) xác định}

= {2x + 1 ≥ 0 và 3 -x ≥ 0} = {x ≥ -1/2 và x ≤ 3} = [-1/2; 3]

Chú ý chỉ cần viết gọn

a) x ≠-1/2 b) x ≠1 và x ≠-3

Giải SGK Toán lớp 10 tập 1 bài 2 trang 38

Cho hàm số: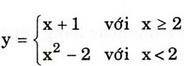 

Tính giá trị của hàm số tại x = 3, x = -1, x = 2.

Hướng dẫn giải bài 2:

Tại x = 3 ≥ 2. Thay x = 3 vào y = x + 1 ta có y = 4

Tại x = -1 < 2. Thay x = -1 vào y = x² - 2, ta có y = (-1)² - 2 = -1

Tại x = 2 ≥ 2. Thay x = 2 vào y = x + 1 ta có y = 3.

Giải bài 3 SGK Toán lớp 10 tập 1 trang 39

Cho hàm số y = 3x² – 2x + 1. Các điểm sau có thuộc đồ thị hay không?

a) M(- 1;6); b) N(1;1); c) P(0;1).

Hướng dẫn giải bài 3:
a) Điểm A(x₀; y₀) thuộc đồ thị (G) của hàm số y = f(x) có tập xác định D khi và chỉ khi: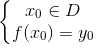 
Tập xác định của hàm số y = 3x² – 2x + 1 là D = R.

Ta có: -1 ∈ R, f(-1) = 3(-1)² – 2(-1) + 1 = 6

Vậy điểm M(-1;6) thuộc đồ thị hàm số đã cho.

b) Ta có: 1 ∈ R, f(1) = 3 (1)² – 2(1) + 1 = 2 ≠1.

Vậy N(1;1) không thuộc đồ thị đã cho.

c) P(0;1) thuộc đồ thị đã cho.

Giải SGK Toán lớp 10 tập 1 trang 39 bài 4

Xét tính chẵn lẻ của hàm số:

a) y = |x|; b) y = (x + 2)²

c) y = x³ + x; d) y = x² + x + 1.

Hướng dẫn giải bài 4:

a) Tập xác định của y = f(x) = |x| là D = R.

∀x ∈ R ⇒ -x ∈ R

f(-x) = |-x| = |x| = f(x)

Vậy hàm số y = |x| là hàm số chẵn.

b) Tập xác định của

y = f(x) = (x + 2)² là R.

x ∈ R ⇒ -x ∈ R

f(-x) = (-x + 2)² = x² – 4x + 4 ≠f(x)

f(-x) ≠-f(x) = -x² – 4x – 4

Vậy hàm số y = (x + 2)² không chẵn, không lẻ.

c) D = R, x ∈ D ⇒ -x ∈ D

f(-x) = (-x³) + (-x) = -(x³ + x) = -f(x)

Vậy hàm số đã cho là hàm số lẻ.

d) Hàm số không chẵn cũng không lẻ.

Kiến thức về hàm số

Định nghĩa

Cho D ∈ R, D ≠Φ. Một hàm số xác định trên D là một quy tắc f cho tương ứng mỗi số x ∈ D với một và duy nhất chỉ một số y ∈ R. Ta kí hiệu:

f: D → R

x → y = f(x)

Tập hợp D được gọi là tập xác định (hay miền xác định) x được gọi là biến số (hay đối số), y₀ = f(x₀) tại x = x₀.

Một hàm số có thể được cho bằng một công thức hay bằng biểu đồ hay bằng bảng.

Lưu ý rằng, khi cho nột hàm số bằng công thức mà không nói rõ tập xác định thì ta ngầm hiểu tập xác định D là tập hợp các số x ∈ R mà các phép toán trong công thức có nghĩa.

Đồ thị

Đồ thị của hàm số: f: D → R

x → y = f(x) là tập hợp các điểm (x; f(x)), x ∈ D trên mặt phẳng tọa độ.

Sự biến thiên

Hàm số y = f(x) là đồng biến trên khoảng (a; b) nếu với mọi x₁, x₂ ∈ (a; b) mà x₁ < x₂ => f(x₁) < f(x₂) hay x1 ≠x₂ ta có .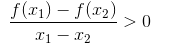

Hàm số y = f(x) là nghịch biến trên khoảng (a; b) nếu với mọi x₁, x₂ ∈ (a; b) mà x1 < x₂ => f(x₁) > f(x₂) hay x₁ ≠x₂ ta có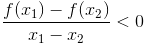 

Tính chẵn lẻ của hàm số

Hàm số f: D → R

x → y = f(x) được gọi là hàm số chẵn nếu: x ∈ D => -x ∈ D và f(-x) = f(x), là hàm số lẻ nếu x ∈ D => -x ∈ D và f(-x) = -f(x).
Đồ thị của hàm số chẵn có trục đối xứng là trục tung. Đồ thị của hàm số lẻ nhận gốc O của hệ trục tọa độ làm tâm đối xứng.

CLICK NGAY vào nút TẢI VỀ dưới đây để tải giải Toán lớp 10 SGK trang 38, 39 file word, file pdf hoàn toàn miễn phí.