Giải bài tập Toán hình 10 trang 40 SGK tập 1 chi tiết nhất

Hướng dẫn giải Toán lớp 10 sách giáo khoa Hình học trang 40 bài: Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ đầy đủ, chi tiết nhất. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị tốt nhất cho bài học sắp tới nhé.

Giải bài 1 SGK Toán hình lớp 10 tập 1 trang 40

Chứng minh rằng trong tam giác ABC có:

a) sin A = sin(B + C)

b) cos A = -cos(B + C)

Lời giải:

a) Trong ΔABC có: A + (B + C) = 180^o hay A = 180^o - (B + C) nghĩa là A và (B + C) bù nhau.

Theo tính chất của hai góc bù nhau thì: sinA = sin(B+C) (đpcm)

b) Tương tự câu a, ta có: cosA = -cos(B+C) (đpcm)

Giải bài 2 trang 40 SGK Toán hình học 10 tập 1

Cho AOB là tam giác cân tại O có OA = a và có các đường cao OH và AK. Giả sử ∠AOH = α. Tính AK và OK theo a và α.

Lời giải:

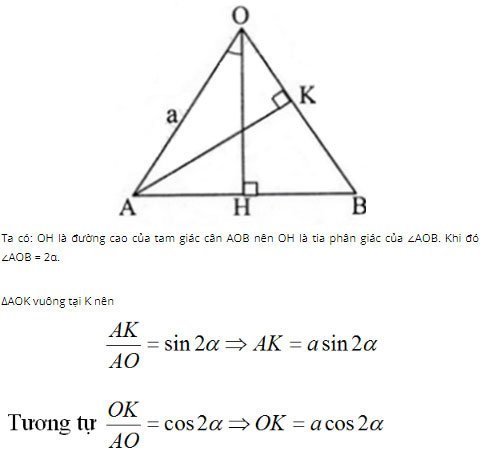
Giải Toán hình sách giáo khoa lớp 10 tập 1 bài 3 trang 40

Chứng minh rằng:

a) sin105^o = sin75^o;

b) cos170^o = -cos10^o;

c) cos122^o = -cos58^o.

Lời giải:

(Áp dụng tính chất lượng giác của hai góc bù nhau)

a) Ta có: 105^o = 180^o - 75^o

Vậy sin105^o = sin75^o;

b) Ta có: 170^o = 180^o - 10^o

Vậy cos170^o = -cos10^o;

c) Ta có: 122^o = 180^o - 58^o

Vậy cos122^o = -cos58

Giải SGK hình học Toán lớp 10 tập 1 trang 40 bài 4

Chứng minh rằng với mọi góc α (0^o ≤ α ≤ 180^o) ta đều có cos²α + sin²α = 1.

Lời giải:

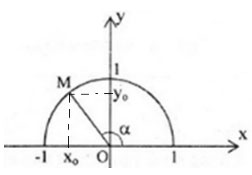
Vẽ đường tròn lượng giác (O; 1). Theo định nghĩa, điểm M(x_o; y_o) thuộc đường tròn có:

sinα = y_o

cosα = x_o

Áp dụng định lí Pitago ta có:

x_o² + y_o² = OM² = 1

⇔ cos²α + sin²α = 1 (đpcm)

Giải bài 5 sách Toán hình học 10 tập 1 trang 40

Cho góc x, với cosx = 1/3. Tính giá trị của biểu thức: P = 3sin²x + cos²x.

Lời giải:

Ta có: sin²x + cos²x = 1

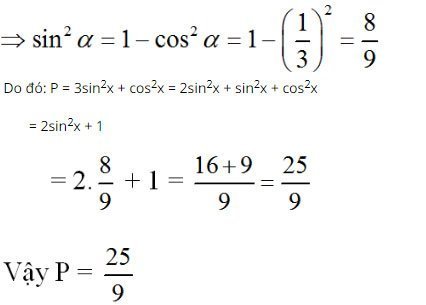
Giải Toán SGK hình lớp 10 tập 1 trang 40 bài 6

Cho hình vuông ABCD. Tính

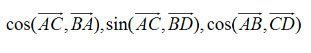
Lời giải

CLICK NGAY vào nút TẢI VỀ dưới đây để giải toán lớp 10 SGK trang 40 file word, pdf hoàn toàn miễn phí.