Giải toán lớp 10 trang 94 SGK tập 1: Dấu của nhị thức bậc nhất

Hướng dẫn giải Toán lớp 10 sách giáo khoa trang 94 bài: Dấu của nhị thức bậc nhất đầy đủ, chi tiết nhất. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị tốt nhất cho bài học sắp tới nhé.

Giải bài 1 SGK Toán lớp 10 tập 1 trang 94

Xét dấu các biểu thức:

Hướng dẫn giải

Lập bảng xét dấu theo quy tắc trong bảng sau:

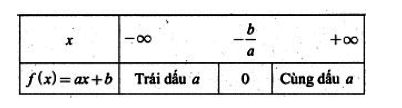
Đáp án và hướng dẫn giải bài 1:

a. Ta lập bảng xét dấu

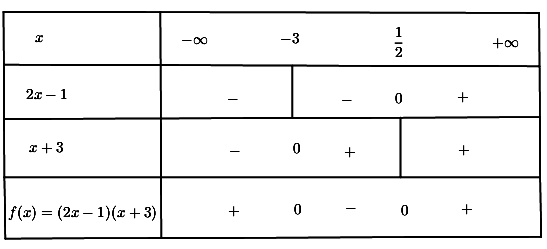
Kết luận: f(x) < 0 nếu – 3 < x < 1/2

f(x) = 0 nếu x = – 3 hoặc x = 1/2

f(x) > 0 nếu x < – 3 hoặc x > 1/2

b) Làm tương tự câu a).

f(x) < 0 nếu x ∈ (-3; -2) ∪ (-1; +∞)

f(x) = 0 với x = -3, -2, -1

f(x) > 0 với x ∈ (-∞; -3) ∪ (-2; -1).

c) Ta có:

Làm tương tự câu b).

f(x) không xác định nếu x = -1/3 hoặc x = 2

 với 

 với 

d) f(x) = 4x² – 1 = (2x – 1)(2x + 1).

f(x) = 0 với x = ± 1/2

f(x) < 0 với x ∈ (1/2; -1/2)

 với 

Giải bài 2 trang 94 SGK Toán lớp 10 tập 1

Giải các bất phương trình:

Hướng dẫn giải

Giải bất phương trình f(x) > 0 thực chất là xét xem biểu thức f(x) nhận giá trị dương với những giá trị nào của x (do đó cũng biết f(x) nhận giá trị âm với những giá trị nào của x). Điều này tương tự với bất phương trình f(x) < 0, 

Bước 1: Tìm tập xác định của BPT.

Bước 2: Chuyển vế, quy đồng phân thức.

Bước 3: Lập bảng xét dấu.

Bước 4: Kết luận nghiệm.

Đáp án và hướng dẫn giải bài 2:

Xét dấu của f(x) ta được tập nghiệm của bất phương trình: 

Từ bảng xét dấu ta thấy f(x) < 0 ⇔ x < -1; 0 < x < 3

Vậy tập nghiệm của bất phương trình: x < -1; 0 < x < 3; x ≠1

c)

Bảng xét dấu:

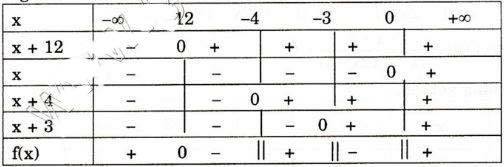
Từ bảng xét dấu ta thấy f(x) < 0 ⇔ -12 < x < 4 hoặc -3 < x < 0

Vậy tập nghiệm của bất phương trình: -12 < x < -4 hoặc -3 < x < 0

d)

Bảng xét dấu:

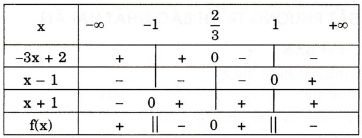
Từ bảng xét dấu ta thấy f(x) < 0 ⇔ -1 < x < 2/3; x > 1

Vậy tập nghiệm của bất phương trình: -1 < x < 2/3; x > 1

Giải bài 3 SGK Toán lớp 10 trang 94 tập 1

Giải các bất phương trình

a) |5x – 4| ≥ 6;

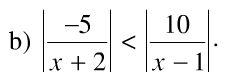
Hướng dẫn giải

Giải bất phương trình f(x) > 0 thực chất là xét xem biểu thức f(x) nhận giá trị dương với những giá trị nào của x (do đó cũng biết f(x) nhận giá trị âm với những giá trị nào của x). Điều này tương tự với bất phương trình f(x) < 0, 

Đáp án và hướng dẫn giải bài 3:

a) <=> (5x – 2)² ≥ 62 <=> (5x – 4)² – 62 ≥ 0

<=> (5x – 4 + 6)(5x – 4 – 6) ≥ 0 <=> (5x + 2)(5x – 10) ≥ 0

Bảng xét dấu:

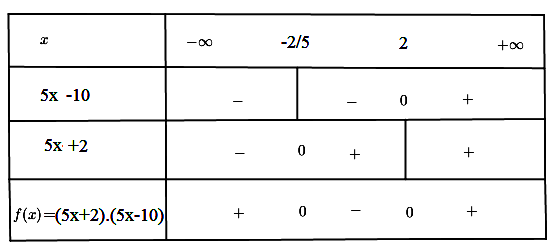
Từ bảng xét dấu cho tập nghiệm của bất phương trình: 

b) 

Bảng xét dấu:

Vậy nghiệm của phương trình là: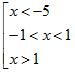 

CLICK NGAY vào nút TẢI VỀ dưới đây để giải toán lớp 10 SGK trang 94 file word, pdf hoàn toàn miễn phí