Giải toán lớp 10 trang 70, 71, 72 SGK tập 1: Ôn tập chương 3

Hướng dẫn cách giải bài tập Toán lớp 10 trang 70, 71, 72 Sách giáo khoa bài Ôn tập chương 3 đầy đủ và chi tiết nhất dưới đây, giúp các bạn học sinh củng cố kiến thức đã được học và vận dụng để có thể giải các dạng toán với yêu cầu tương tự như vậy.

Giải bài 1 trang 70 SGK Toán lớp 10 tập 1

Khi nào hai phương trình được gọi là tương đương? Cho ví dụ.

Hướng dẫn giải bài 1:

Hai phương trình được gọi là tương đương khi chúng có chung tập nghiệm. Ví dụ:

• x² – 1 = 0 và (x + 1)(x – 1) = 0 là hai phương trình tương đương
• sinx = 2 và x² + 1 = 0 là hai phương trình tương đương (vì sao?)

Giải Toán SGK lớp 10 tập 1 trang 70 bài 2

Thế nào là phương trình hệ quả? Cho ví dụ.

Hướng dẫn giải bài 2:

Cho hai phương trình f(x) = g(x) và f₁(x) = g₁(x). Nếu mọi nghiệm của f(x) = g(x) đều là nghiêm của f₁(x) = g₁(x) thì phương trình f₁(x) = g₁(x) được gọi là phương trình hệ quả của phương trình f(x) = g(x)

Ví du: Cho x² – 2x – 3 = 0 và (x + 1)(x – 3)x thì (x + 1)(x – 3)x = 0 là phương trình hệ của phương trình: x² + 2x – 3 = 0

Thật vậy, gọi T là tập nghiệm của x² – 2x – 3 = 0 thì T = {-1; 3}; T1 là tập nghiệm của (x + 1)(x - 3)x = 0 thì T₁ = {-1; 3; 0}. Ta thấy T ⊂ T₁

Giải bài 3 trang 70 SGK Toán lớp 10 tập 1

Giải các phương trình sau:

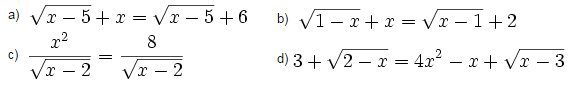
Đáp án và hướng dẫn giải bài 3:

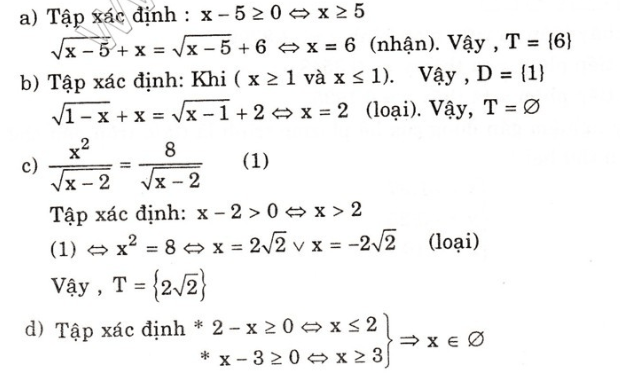
Vậy, D = Ø

Tập nghiệm: T = Ø

Giải bài 4 SGK Toán lớp 10 tập 1 trang 70

Giải các phương trình:

Đáp án và hướng dẫn giải bài 4:

a)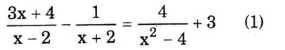 

Tập xác định: x² – 4 ≠0 ⇔ x ≠±2

Quy đồng và bỏ mẫu chung

(1) ⇔ (3x + 4)(x + 2) – (x - 2) = 4 + 3(x² – 4) ⇔ x = -2 (loại)

Vậy, T = Ø

b)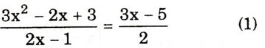 

Tập xác định x ≠1/2

Quy đồng và bỏ mẫu chung 2(2x – 1)

(1) ⇔ 2(3x² – 2x + 3) = (2x - 1)(3x - 5) ⇔ x = -1/9 (nhận)

Vậy, T = (-1/9)

c)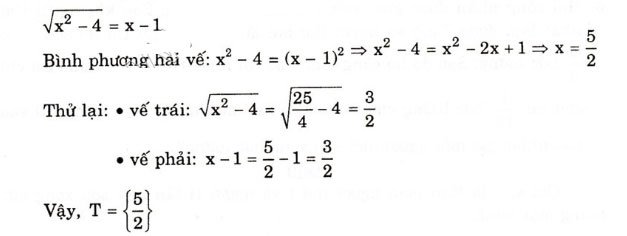 

Giải SGK Toán 10 tập 1 bài 5 trang 70

Giải các hệ phương trình:

Đáp án và hướng dẫn giải bài 5:

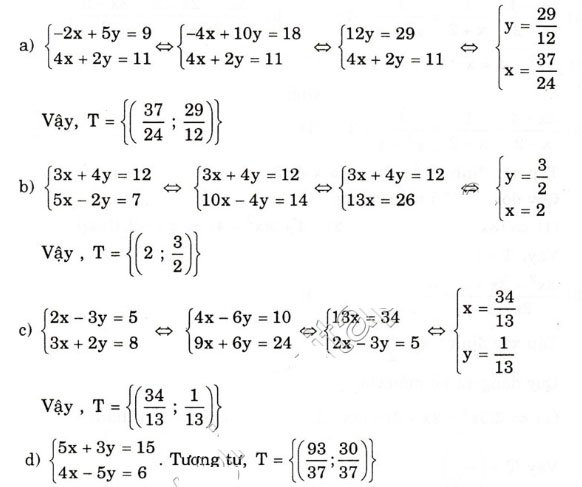
Giải bài 6 trang 70 SGK Toán lớp 10 tập 1

Hai công nhân được giao việc sơn một bức tường. Sau khi người thứ nhất làm được 7 giờ và người thứ hai làm được 4 giờ thì họ sơn được 5/9 bức tường. Sau đó họ cùng làm với nhau trong 4 giờ nữa thì chỉ còn lại 1/18 bức tường chưa sơn. Hỏi nếu mỗi người làm riêng thì sau bao nhiêu giờ mỗi người mới sơn xong bức tường?

Đáp án và hướng dẫn giải bài 6:

Gọi x, y là thời gian người thứ I và người thứ II lần lượt sơn xong bức tường một mình.

• Trong 1 giờ, người thứ I sơn được 1/x (bức tường) nên trong 7 giờ, người thứ I sơn được 7/x (bức tường)
• Tương tự, trong 4 giờ, người thứ II sơn được: 4/y (bức tường)
• Theo đề bài ta có phương trình: 7/x + 4/y = 5/9 (1)
• Sau 4 giờ làm chung, phân số biểu thị số bức tường phải sơn là: 4/9 - 1/18 = 7/18 (bức tường)
• Ta có phương trình: 4(1/x + 1/y) = 7/18 (bức tường) ⇔ 1/x + 1/y = 7/72 (2)

Giải hệ (1) và (2), ta được x = 18 (giờ); y = 24 (giờ)

Vậy, công nhân thứ nhất sơn xong bức tường mất 18 giờ; công nhân thứ hai sơn xong bức tường mất 24 giờ.

Giải bài 7 SGK Toán lớp 10 trang 70 tập 1

Giải các hệ phương trình:

Đáp án và hướng dẫn giải bài 7:

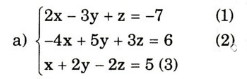
Khử z giữa (1) và (2), ta được 10x – 14y = -27 (4)

Khử z giữa (1) và (3), ta được 5x – 4y = -9 (5)

Từ (4) và (5) ta được x = -0,6; y = 1,5

Thay x = -0,6; y =1,5 vào (1), ta được z = -1,3

Vậy nghiệm của hệ phương trình đã cho là (x; y; z) = (-0,6; 1,5; -1,3).

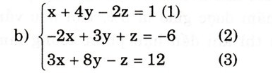
Khử z giữa (1) và (2), ta được -3x + 10y = -11 (4)

Khử z giữa (1) và (3), ta được -5x - 12y = -23 (5)

Từ (4) và (5), ta được x = 4,2; y = 0,16

Thay x = 4,2; y = 0,16 vào (1), ta được z = 1,92

Vậy nghiệm của hệ đã cho là (x; y; z) = (4,2; 0,16; 1,92)

Giải Toán SGK lớp 10 tập 1 bài 8 trang 71

Ba phân số đều có tử số là 1 và tổng của ba phân số đó là bằng 1. Hiệu của phân số thứ nhất và phân số thứ hai bằng phân số thứ ba, còn tổng của phân số thứ nhất và phân số thứ hai bằng 5 lần phân số thứ ba. Tìm các phân số đó.

Đáp án và hướng dẫn giải bài 8:

Gọi 1/a là phân số thứ nhất cần tìm (a > 0)

1/b là phân số thứ hai cần tìm (b > 0)

1/c là phân số thứ ba cần tìm (c > 0)

Theo đề ra, ta có hệ phương trình: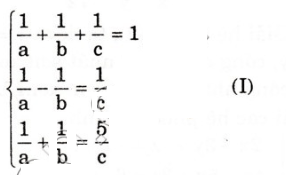 

Đặt x = 1/a; y = 1/b; z = 1/c. Khi đó, hệ (I) trở thành

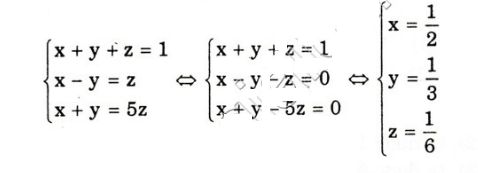
Vậy ba phân số cần tìm là 1/2; 1/3; 1/6.

Giải bài 9 trang 71 SGK Toán lớp 10 tập 1

Một phân xưởng được giao sản xuất 360 sản phẩm trong một số ngày nhất định. Vì phân xưởng tăng năng suất, mỗi ngày làm thêm được 9 sản phẩm so với định mức, nên trước khi hết thời hạn một ngày thì phân xưởng đã làm vượt số sản phẩm được giao là 5%. Hỏi nếu vẫn tiếp tục làm việc với năng suất đó thì khi đến hạn phân xưởng làm được tất cả bao nhiêu sản phẩm?

Đáp án và hướng dẫn giải bài 9:

Gọi x là số ngày dự định làm xong kế hoạch (x > 0)

Khi đó, số sản phẩm dự định làm trong một ngày là 360/x

Số sản phẩm thực tế làm được trong một ngày là 360/x + 9 (sản phẩm)

Số ngày thực tế làm xong kế hoạch là x – 1 (ngày)

Theo bài ra ta có phương trình

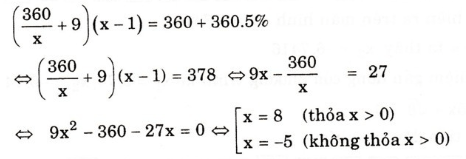
Vậy số ngày dự định làm xong kế hoạch là 8 ngày. Do đó nếu vẫn tiếp tục làm với năng suất thực tế thì trong 8 ngày, phân xưởng đó làm được tất cả: (360/8 + 9)8 = 432 (sản phẩm).

Giải bài 10 SGK Toán lớp 10 tập 1 trang 71

Giải các phương trình sau bằng máy tính bỏ túi

a) 5x² – 3x – 7 = 0; b) 3x² + 4x + 1 = 0;

c) 0,2x² + 1,2x – 1 = 0; d) √2x² + 5x + √8 = 0;

Đáp án và hướng dẫn giải bài 10:

Giải SGK Toán lớp 10 tập 1 trang 71 bài 11

Giải các phương trình

a) |4x – 9| = 3 – 2x

b) |2x + 1| = |3x + 5|

Đáp án và hướng dẫn giải bài 11:

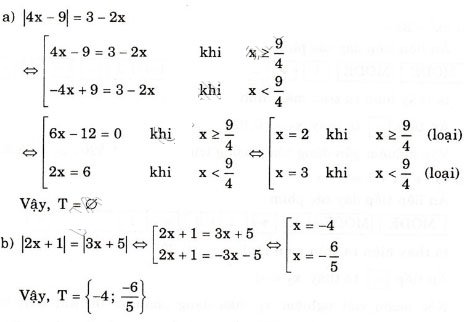
Giải Toán SGK lớp 10 tập 1 trang 71 bài 12

Tìm hai cạnh của mảnh vườn hình chữ nhật trong hai trường hợp

a) Chu vi là 94,4 m và diện tích là 494.55 m²

b) Hiệu của hai cạnh là 12,1 m và diện tích là 1089 m²

Đáp án và hướng dẫn giải bài 12:

a) Gọi x và y là hai kích thước của hình chữ nhật, ta có:

Giải bài 13 trang 71 SGK Toán lớp 10 tập 1

Hai người quét sân. Cả hai người cùng quét sân hết 1 giờ 20 phút, trong khi nếu chỉ quét một mình thì người thứ nhất quét hết nhiều hơn 2 giờ so với người thứ hai. Hỏi mỗi người quét sân một mình hết mấy giờ?

Đáp án và hướng dẫn giải bài 13:

• Gọi x (giờ) là thời gian người thứ nhất quét sân một mình (x > 2)
• Khi đó, x - 2 (giờ) là thời gian người thứ hai quét sân một mình
• Trong 1 giờ, người thứ nhất quét được: 1/x (sân); người thứ hai quét được: 1/(x - 2) (sân)
• Vì cả hai người cùng quét sân hết 1 giờ 20 phút = 4/3 giờ, nên trong 1 giờ làm được: 3/4 (sân)
• Ta có phương trình:

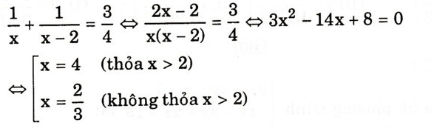
Vậy thời gian người thứ nhất quét sân một mình là 4 giờ, do đó người thứ hai quét một mình hết 2 giờ.

Giải Toán SGK lớp 10 tập 1 bài 14 trang 71

Điều kiện của phương trình 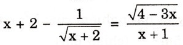 là:

(A) x > -2 và x ≠– 1 (B) x > -2 và x < 4/3

(C) x > -2, x ≠-1 và x ≤ 4/3 (D) x ≠-2 và x ≠-1.

Đáp án và hướng dẫn giải bài 14:

Đáp án đúng là: (C).

Điều kiện:

√4 - 3x có nghĩa ⇔ x ≤ 4/3;

√x + 2 có nghĩa ⇔ x > -2; x + 1 ≠0 ⇔ x ≠-1

Vậy D = {x/x ≤ 4/3l x > -2; x ≠-1}

Giải bài 15 SGK Toán lớp 10 tập 1 trang 72

Tập nghiệm của phương trình trong 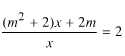 trường hợp m ≠0 là:
(A) {-2/m} (B) ø

(C) R (D) R\{0}

Đáp án và hướng dẫn giải bài 15:

Đáp án đúng là: (A).

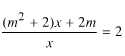 (m ≠0)

⇔ m2x + 2m = 0 ⇔ mx = -2 ⇔ x = -2/m. Vậy T = {-2/m}

Giải SGK Toán lớp 10 tập 1 trang 72 bài 16

Nghiệm của hệ phương trình 

(A) (-39/26; 3/13) (B) (-17/13; -5/13)

(C) (39/26; 1/2) (D) (-1/3; 17/6)

Đáp án bài 16:

Đáp án đúng là: (C).

Giải bài 17 SGK Toán lớp 10 tập 1 trang 72

Nghiệm của hệ phương trình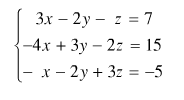 

(A) (-10;7;9) (B) (3/2; -2; 3/2)

(C) -1/4; -9/2; 5/4) (D) (-5; -7; -8)

Đáp án bài 17:

Đáp án đúng là: (D).

CLICK NGAY vào nút TẢI VỀ dưới đây để tải giải Toán lớp 10 SGK trang 70, 71, 72 file word, file pdf hoàn toàn miễn phí.