Giải toán lớp 10 trang 62, 63 SGK tập 1 chi tiết nhất

 

Hướng dẫn giải Toán lớp 10 sách giáo khoa trang 62, 63 bài Phương trình quy về phương trình bậc nhất, bậc hai đầy đủ, chi tiết nhất. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị tốt nhất cho bài học sắp tới nhé.

Giải bài 1 SGK Toán lớp 10 tập 1 trang 62

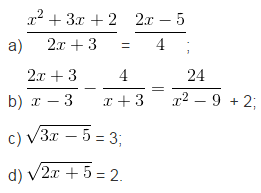
Giải bài 1:

a) ĐKXĐ:

2x + 3 ≠0 ⇔ x ≠-3/2.

Quy đồng mẫu thức rồi khử mẫu thức chung thì được

4(x² + 3x + 2) = (2x – 5)(2x + 3) => 12x + 8 = – 4x – 15

=> x = -23/16 (nhận).

b) ĐKXĐ: x ≠± 3. Quy đồng mẫu thức rồi khử mẫu thì được

(2x + 3)(x + 3) – 4(x – 3) = 24 + 2(x² - 9)

=> 5x = -15 => x = -3 (loại). Phương trình vô nghiệm.

c) Bình phương hai vế thì được: 3x – 5 = 9 => x = 14/3 (nhận).

d) Bình phương hai vế thì được: 2x + 5 = 4 => x = – 1/2.

Giải bài 2 trang 62 SGK Toán lớp 10 tập 1

Giải và biện luận các phương trình sau theo tham số m

a) m(x – 2) = 3x + 1;

b) m²x + 6 = 4x + 3m;

c) (2m + 1)x – 2m = 3x – 2.

Giải bài 2:

a) ⇔ (m – 3)x = 2m + 1.

• Nếu m ≠3 phương trình có nghiệm duy nhất x = (2m + 1)/(m - 3).
• Nếu m = 3 phương trình trở thành 0x = 7. Vô nghiệm.

b) ⇔ (m² – 4)x = 3m – 6.

• Nếu m² – 4 ≠0 ⇔ m ≠± 2, có nghiệm x = (3m - 6)/(m2 – 4) = 3/(m + 2).
• Nếu m = 2, phương trình trở thành 0x = 0, mọi x ∈ R đều nghiệm đúng phương trình.
• Nếu m = -2, phương trình trở thành 0x = -12. Vô nghiệm.

c) ⇔ 2(m – 1)x = 2(m - 1).

• Nếu m ≠1 có nghiệm duy nhất x = 1.
• Nếu m = 1 mọi x ∈ R đều là nghiệm của phương trình.

Giải bài 3 SGK Toán lớp 10 trang 62 tập 1

Có hai rổ quýt chứa số quýt bằng nhau. Nếu lấy 30 quả ở rổ thứ nhất đưa sang rổ thứ hai thì số quả ở rổ thứ hai bằng 1/3 của bình phương số quả còn lại ở rổ thứ nhất. Hỏi số quả quýt ở mỗi rổ lúc ban đầu là bao nhiêu?

Giải bài 3:

Gọi x là số quýt chứa trong một rổ lúc đầu. Điều kiện x nguyên, x > 30. Ta có phương trình 1/3(x – 30)² = x + 30 ⇔ x² – 3x + 810 = 0 ⇔ x = 45 (nhận), x = 18 (loại).

Trả lời: Số quýt ở mỗi rổ lúc đầu: 45 quả.

Giải SGK Toán 10 tập 1 bài 4 trang 62

Giải các phương trình

a) 2x⁴ – 7x² + 5 = 0;

b) 3x⁴ + 2x² – 1 = 0.

Giải bài 4:

a) Đặt x² = t ≥ 0 ta được 2t² – 7t + 5 = 0, t ≥ 0

2t² – 7t + 5 = 0 ⇔ t₁ = 1 (nhận), t₂ = 5/2 (nhận).

Suy ra nghiệm của phương trình ẩn x là x_1,2 = ±1, x_3,4 = ±√10/2.

b) Đặt x² = t ≥ 0 thì được 3t² + 2t – 1 = 0 ⇔ t₁ = -1 (loại), t₂ = 1/3 (nhận).

Suy ra nghiệm của phương trình ẩn x là x_1,2 = ±√3/3

Giải bài 5 trang 62 SGK Toán lớp 10 tập 1

Giải các phương trình sau bằng máy tính bỏ túi (làm tròn kết quả đến chữ số thập phân thứ ba)

a) 2x² – 5x + 4 = 0;

b) -3x² + 4x + 2 = 0;

c) 3x² + 7x + 4 = 0;

d) 9x² – 6x – 4 = 0.

Giải bài 5:

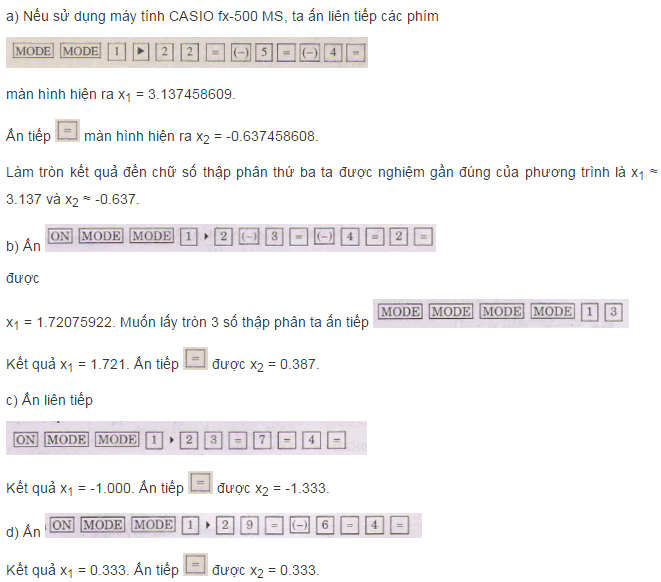
Giải Toán SGK lớp 10 tập 1 bài 6 trang 62

Giải các phương trình.

a) |3x – 2| = 2x + 3;

b) |2x -1| = |-5x – 2|;

c) (x - 1)/(2x - 3) = (-3x + 1)/(|x + 1|)

d) |2x + 5| = x² + 5x + 1.

Giải bài 6:

a) ĐKXĐ: 2x + 3 ≥ 0. Bình phương hai vế thì được:

(3x – 2)² = (2x + 3)² => (3x – 2)² – (2x + 3)² = 0

⇔ (3x - 2 + 2x + 3)(3x – 2 – 2x – 3) = 0

=> x₁ = -1/5 (nhận), x₂ = 5 (nhận)

Tập nghiệm S = {-1/5; 5}.

b) Bình phương hai vế:

(2x – 1)² = (5x + 2)² => (2x – 1 + 5x + 2)(2x – 1 – 5x – 2) = 0

=> x₁ = -1/7, x₂ = -1.

c) ĐKXĐ: x ≠3/2, x ≠-1. Quy đồng rồi khử mẫu thức chung

(x – 1)|x + 1| = (2x – 3)(-3x + 1)

• Với x ≥ -1 ta được: x² – 1 = -6x² + 11x – 3 => x₁ = (11 – √65)/14; x₂ = (11 + √65)/14.
• Với x < -1 ta được: -x² + 1 = -6x² + 11x – 3 => x₁ = (11 – √41)/10 (loại vì không thỏa mãn đk x < -1); x₂ = (11 + √41)/10 (loại vì x > -1)

Kết luận: Tập nghiệm S = {(11 – √65)/14; (11 + √65)/14}

d) ĐKXĐ: x² + 5x + 1 > 0

• Với x ≥ -5/2 ta được: 2x + 5 = x² + 5x + 1 => x₁ = -4 (loại); x₂ = 1 (nhận)
• Với x < -5/2 ta được: -2x – 5 = x² + 5x + 1 => x₁ = -6 (nhận); x₂ = -1 (loại).

Kết luận: Tập nghiệm S = {1; -6}.

Giải bài 7 SGK Toán lớp 10 tập 1 trang 62

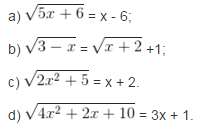
Giải bài 7:

a) ĐKXĐ: x – 6 ≥ 0 ⇔ x > 6. Bình phương hai vế thì được 5x + 6 = (x – 6)² ⇔ x₁ = 2 (loại), x₂ = 15 (nhận).

b) ĐKXĐ: – 2 ≤ x ≤ 3. Bình phương hai vế thì được 3 – x = x + 3 + 2√(x + 2) ⇔ -2x = 2√(x + 2).

Điều kiện x ≤ 0. Bình phương tiếp ta được: x² = x + 2 => x₁ = -1 (nhận); x₂ = 2 (loại).

Kết luận: Tập nghiệm S {-1}.

c) ĐKXĐ: x ≥ -2.

=> 2x² + 5 = (x + 2)² => x² – 4x + 1 = 0

=> x₁ =2 – √3 (nhận), x₂ = 2 + √3 (nhận).

d) ĐK: x ≥ -1/3.

=> 4x² + 2x + 10 = (3x + 1)² => x₁ = -9/5 (loại), x₂ = 1 (nhận).

Giải Toán SGK lớp 10 tập 1 trang 63 bài 8

Cho phương trình 3x² – 2(m + 1)x + 3m – 5 = 0.

Xác định m để phương trình có một nghiệm gấp ba nghiệm kia. Tính các nghiệm trong trường hợp đó.

Giải bài 8:

Giả sử phương trình có hai nghiệm x₁ và x₂ với x₂ = 3x₁. Theo định lí Viet ta có:

x₁ + x₂ = 4 x₁ = [2(m + 1)]/3 => x₁ = (m + 1)/6.

Thay x₁ = (m + 1)/6 vào phương trình ta được 3[(m + 1)/6]² - 2(m + 1).(m + 1)/6 + 3m – 5 = 0

⇔ -3m² + 30m – 63 = 0 ⇔ m₁ =3, m₂ =7.

Thay m = 3 vào phương trình ta thấy pt có hai nghiệm x₁ = 2/3; x₂ = 2.

Với m = 7 ta có hai nghiệm x₁ = 4/3; x₂ = 4.

CLICK NGAY vào nút TẢI VỀ dưới đây để giải toán lớp 10 SGK trang 62, 63 file word, pdf hoàn toàn miễn phí