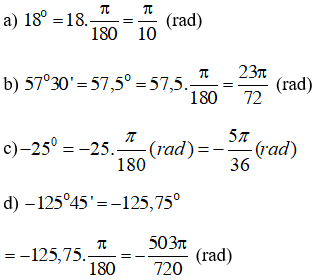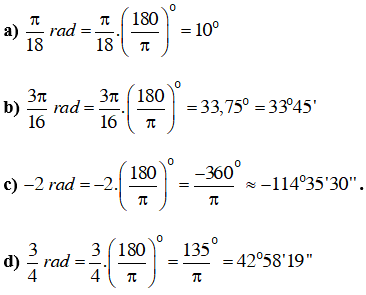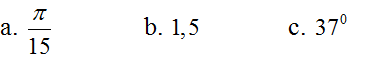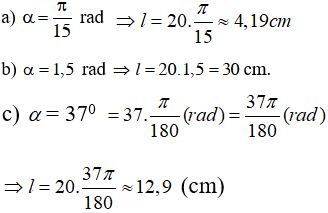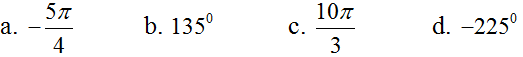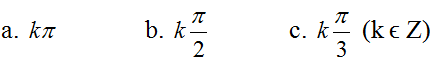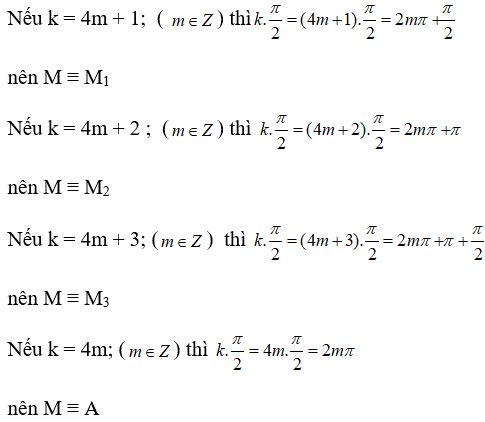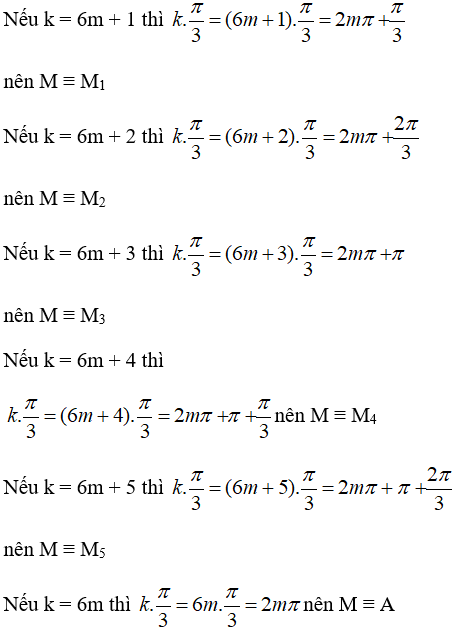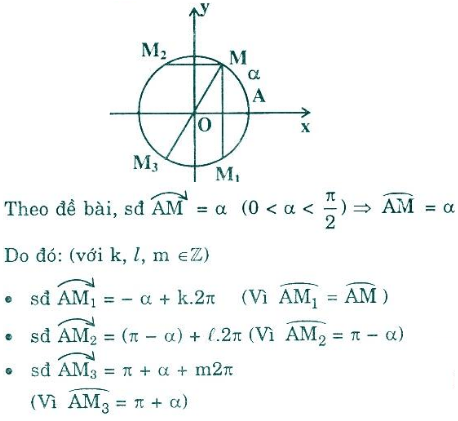Giải toán lớp 10 trang 140 SGK tập 1: Cung và góc lượng giác

Hướng dẫn giải Toán lớp 10 trang 140 Sách giáo khoa bài: Cung và góc lượng giác đầy đủ, chi tiết nhất. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị tốt nhất cho bài học sắp tới nhé.

Giải bài 1 trang 140 SGK Toán lớp 10 tập 1

Khi biểu diễn các cung lượng giác có số đo khác nhau trên đường tròn lượng giác, có thể xảy ra trường hợp các điểm cuối của chúng trùng nhau không ? Khi nào trường hợp này xảy ra ?

Lời giải:

Khi số đo hai cung lệch nhau k.2π (k ∈ Z) thì điểm cuối của chúng có thể trùng nhau.

Chẳng hạn các cung α = π/3 và β = π/3 + 2π , γ = π/3 - 2π có điểm cuối trùng nhau khi biểu diễn trên đường tròn lượng giác.

Giải bài 2 SGK Toán lớp 10 trang 104 tập 1

Đổi số đo của các số sau đây ra radian

a. 18°

b.57°30’

c. – 25°

d. -125°45’

Lời giải

Giải bài 3 SGK Toán lớp 10 tập 1 trang 140

Đổi số đo của các cung sau đây ra độ, phút, giây

Lời giải

Giải SGK Toán lớp 10 tập 1 bài 4 trang 140

Một đường tròn có bán kính 20cm. Tìm độ dài các cung trên đường tròn, có số đo

Lời giải

Từ công thức l = Rα (α có đơn vị là rad) ta có:

Giải bài 5 trang 140 SGK Toán lớp 10 tập 1

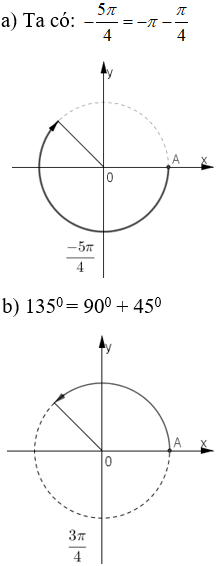
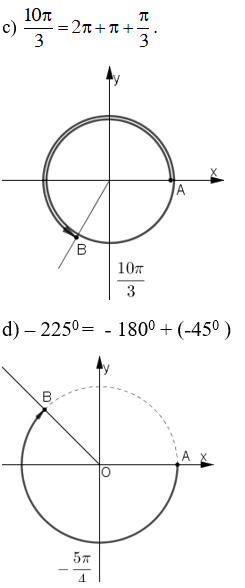
Trên đường tròn lượng giác hãy biểu diễn các cung có số đo

Lời giải

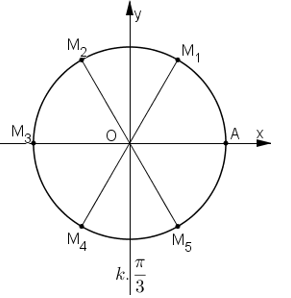
Giải Toán SGK lớp 10 tập 1 trang 140 bài 6

Trên đường tròn lượng giác gốc A, xác định các điểm M khác nhau biết rằng cung AM có số đo tương ứng là (trong đó k là một số nguyên tùy ý)

Lời giải

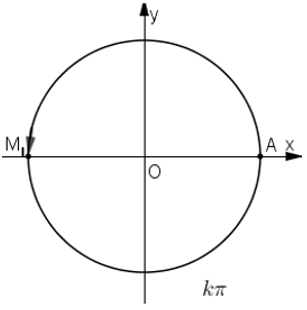
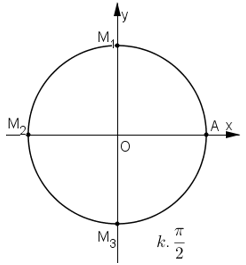
a) Nếu k = 2n +1 (n ∈ Z) (thì kπ = (2n + 1)π = 2nπ + π nên M ≡ M₁

Nếu k = 2n (n ∈ Z) thì kπ = 2nπ nên M ≡ A

b)

c)

Giải Toán SGK lớp 10 tập 1 trang 140 bài 7

Trên đường tròn lượng giác cho điểm M xác định bởi sđ cung AM = α (0 < α < π/2). Gọi M₁, M₂, M₃ lần lượt là điểm đối xứng của M qua trục Ox, trục Oy và gốc tọa độ. Tìm số đo các cung AM₁, AM₂, AM₃.

Lời giải

CLICK NGAY vào nút TẢI VỀ dưới đây để giải toán lớp 10 SGK trang 140 file word, pdf hoàn toàn miễn phí.