Logo

Giải SBT Toán 10 trang 106 tập 1 bài: Bất đẳng thức

Giải SBT Toán lớp 10 trang 106 tập 1 bài: Bất đẳng thức đầy đủ hỗ trợ các em học sinh củng cố kiến thức và hiểu rõ phương pháp giải các dạng bài tập trong sách bài tập
5.0
1 lượt đánh giá

Nội dung bài viết

  1. Giải bài 1 trang 106 sách bài tập Toán lớp 10 tập 1 
  2. Giải Toán lớp 10 SBT tập 1 bài 2 trang 106
  3. Giải bài 3 SBT Toán lớp 10 tập 1 trang 106
  4. Giải SBT Toán lớp 10 tập 1 bài 4 trang 106
  5. Giải bài 5 sách bài tập Toán 10 tập 1 trang 106
  6. Giải bài 6 SBT Toán 10 tập 1 trang 106
  7. Giải SBT Toán 10 tập 1 bài 7 trang 106
  8. Giải bài 8 Toán lớp 10 SBT tập 1 trang 106
  9. Giải bài 9 trang 106 sách bài tập Toán 10 tập 1
  10. Giải SBT Toán lớp 10 tập 1 bài 10 trang 106
  11. Giải sách bài tập Toán 10 tập 1 bài 11 trang 106
  12. Giải bài 12 SBT Toán 10 tập 1 trang 106
  13. Giải SBT Toán 10 tập 1 bài 13 trang 106
  14. Giải Toán lớp 10 sách bài tập tập 1 bài 14 trang 106

Giải sách bài tập Toán 10 tập 1 bài 1 chương 4: Bất đẳng thức được giải đáp chi tiết và rõ ràng nhất, giúp cho các bạn học sinh có thể tham khảo và chuẩn bị tốt nhất cho bài học sắp tới nhé.

Giải bài 1 trang 106 sách bài tập Toán lớp 10 tập 1 

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

{x^4} + {y^4} \ge {x^3}y + x{y^3}

Lời giải:

{x^4} + {y^4} \ge {x^3}y + x{y^3} \Leftrightarrow {x^4} + {y^4} - {x^3}y - x{y^3} \ge 0

\Leftrightarrow {x^3}(x - y) + {y^3}(y - x) \ge 0 \Leftrightarrow (x - y)({x^3} - {y^3}) \ge 0

\Leftrightarrow {(x - y)^2}({x^2} + {y^2} + xy) \ge 0 \Leftrightarrow {(x - y)^2}({(x + {y \over 2})^2} + {{3{y^2}} \over 4}) \ge 0 (đúng)

Giải Toán lớp 10 SBT tập 1 bài 2 trang 106

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

{x^2} + 4{y^2} + 3{z^2} + 14 > 2x + 12y + 6z

Lời giải:

{x^2} + 4{y^2} + 3{z^2} + 14 > 2x + 12y + 6z

\Leftrightarrow {x^2} - 2x + 4{y^2} - 12y + 3({z^2} - 2z) + 14 > 0

\Leftrightarrow {(x - 1)^2}{(2y - 3)^2} + 3{(z - 1)^2} + 1 > 0 (đúng)

Giải bài 3 SBT Toán lớp 10 tập 1 trang 106

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

{a \over {\sqrt b }} + {b \over {\sqrt a }} \ge \sqrt a + \sqrt b

Lời giải:

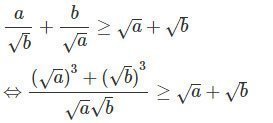
Giải bài tập Toán 10 SBT bài 1 chương 4

\Leftrightarrow (\sqrt a + \sqrt b )(a + b - \sqrt {ab} ) \ge (\sqrt a + \sqrt b )\sqrt {ab}

\Leftrightarrow (\sqrt a + \sqrt b )(a + b - 2\sqrt {ab} ) \ge 0

\Leftrightarrow (\sqrt a + \sqrt b ){(\sqrt a - \sqrt b )^2} \ge 0 (đúng)

Giải SBT Toán lớp 10 tập 1 bài 4 trang 106

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

{1 \over a} + {1 \over b} \ge {4 \over {a + b}}

Lời giải:

Từ {1 \over a} + {1 \over b} \ge 2\sqrt {{1 \over {ab}}} và a + b \ge 2\sqrt {ab} suy ra

(a + b)({1 \over a} + {1 \over b}) \ge 4 hay {1 \over a} + {1 \over b} \ge {4 \over {a + b}}

Giải bài 5 sách bài tập Toán 10 tập 1 trang 106

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

{{a + b + c + d} \over 4} ≥ \sqrt[4]{abcd}

Lời giải:

Từ a + b \ge 2\sqrt {ab} và c + d \ge 2\sqrt {cd} suy ra

a + b + c + d \ge 2(\sqrt {ab} + \sqrt {cd} )

= > 2.2\sqrt {\sqrt {ab} .\sqrt {cd} }

=> {{a + b + c + d} \over 4} ≥ \sqrt[4]{abcd}

=> a + b + c + d \ge 2.2\sqrt {\sqrt {ab} .\sqrt {cd} }

=> {{a + b + c + d} \over 4} ≥ \sqrt[4]{abcd}

Giải bài 6 SBT Toán 10 tập 1 trang 106

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

{1 \over a} + {1 \over b} + {1 \over c} + {1 \over d} \ge {{16} \over {a + b + c + d}}

Lời giải:

Từ a + b + c + d \ge \sqrt[4]{abcd}

{1 \over a} + {1 \over b} + {1 \over c} + {1 \over d} \ge 4\sqrt[4]{\frac{1}{abcd}}

Suy ra (a + b + c + d)({1 \over a} + {1 \over b} + {1 \over c} + {1 \over d}) \ge 16

Hay {1 \over a} + {1 \over b} + {1 \over c} + {1 \over d} \ge {{16} \over {a + b + c + d}}

Giải SBT Toán 10 tập 1 bài 7 trang 106

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

{a^2}b + {1 \over b} \ge 2a

Lời giải:

{a^2}b + {1 \over b} \ge 2\sqrt {{a^2}b.{1 \over b}} = 2a

Giải bài 8 Toán lớp 10 SBT tập 1 trang 106

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

(a + b)(b + c)(c + a) \ge 8abc

Lời giải:

Từ a + b \ge 2\sqrt {ab} ,b + c \ge 2\sqrt {bc} ,c + a \ge 2\sqrt {ca}

Suy ra: (a + b)(b + c)(c + a) \ge 8abc

Giải bài 9 trang 106 sách bài tập Toán 10 tập 1

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

{(\sqrt a + \sqrt b )^2} \ge 2\sqrt {2(a + b)\sqrt {ab} }

Lời giải:

{(\sqrt a + \sqrt b )^2} = a + b + 2\sqrt {ab} \ge 2\sqrt {(a + b).2\sqrt {ab} }

Giải SBT Toán lớp 10 tập 1 bài 10 trang 106

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

{1 \over a} + {1 \over b} + {1 \over c} \ge {9 \over {a + b + c}}

Lời giải:

(a + b + c)({1 \over a} + {1 \over b} + {1 \over c}) = 1 + 1 + 1 + ({a \over b} + {b \over a}) + ({a \over c} + {c \over a}) + ({b \over c} + {c \over b})

\ge 3 + 2 + 2 + 2 = 9 = > {1 \over a} + {1 \over b} + {1 \over c} \ge {9 \over {a + b + c}}

Giải sách bài tập Toán 10 tập 1 bài 11 trang 106

Tìm giá trị nhỏ nhất của hàm số

y = {4 \over x} + {9 \over {1 - x}} với 0 < x < 1.

Lời giải:

y = {{4(x + 1 - x)} \over x} + {{9(x + 1 - x)} \over {1 - x}}

=4 + 9 + {{4(1 - x)} \over x} + 9.{x \over {1 - x}} \ge 13 + 2\sqrt {4.{{(1 - x)} \over x}.9.{x \over {1 - x}}} = 25

=> y \ge 25,\forall x \in (0;1)

Đẳng thức y = 25 xảy ra khi và chỉ khi

\left\{ \matrix{{{4(1 - x)} \over x} = {{9x} \over {1 - x}} = 6 \hfill \cr x \in (0;1) \hfill \cr} \right.

hay x = {2 \over 5}

Vậy giá trị nhỏ nhất của hàm số đã cho bằng 25 đạt tại x = {2 \over 5}

Giải bài 12 SBT Toán 10 tập 1 trang 106

Tìm giá trị lớn nhất của hàm số

y = 4{x^3} - {x^4} với 0 \le x \le 4

Lời giải:

y = 4{x^3} - {x^4} = {x^3}(4 - x)

=> 3y = x.x.x(12 - 3x) \le {({{x + x} \over 2})^2}{({{x + 12 - 3x} \over 2})^2}

= > 48 \le {{\rm{[}}2x(12 - 2x){\rm{]}}^2} \le {({{2x + 12 - 2x} \over 2})^4} = {6^4}

= > y \le {{{6^4}} \over {48}} = 27,\forall x \in {\rm{[}}0;4]

y = 27 \Leftrightarrow \left\{ \matrix{x = x \hfill \cr x = 12 - 3x \hfill \cr 2x = 12 - x \hfill \cr x \in {\rm{[}}0;4] \hfill \cr} \right. \Leftrightarrow x = 3

Vậy giá trị lớn nhất của hàm số đã cho bằng 27 đạt được khi x = 3.

Giải SBT Toán 10 tập 1 bài 13 trang 106

Tìm giá trị lớn nhất, nhỏ nhất của hàm số sau trên tập xác định của nó

y = \sqrt {x - 1} + \sqrt {5 - x}

Lời giải:

Vế phải có nghĩa khi 1 \le x \le 5

Ta có: {y^2} = {(\sqrt {x - 1} + \sqrt {5 - x} )^2} = 4 + 2\sqrt {(x - 1)(5 - x)}

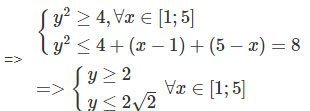
Giải bài tập Toán 10 SBT bài 1 chương 4

Hơn nữa y = 2 \Leftrightarrow (x - 1)(5 - x) = 0 \Leftrightarrow \left[ \matrix{x = 1 \hfill \cr x = 5 \hfill \cr} \right.$

y = 2\sqrt 2 \Leftrightarrow x - 1 = 5 - x \Leftrightarrow x = 3

Vậy giá trị lớn nhất của hàm số đã cho bằng 2\sqrt 2 khi x = 3, giá trị nhỏ nhất của hàm số đã cho bằng 2 khi x = 1 hoặc x = 5.

Giải Toán lớp 10 sách bài tập tập 1 bài 14 trang 106

Chứng minh rằng:

\left| {x - z} \right| \le \left| {x - y} \right| + \left| {y - z} \right|,\forall x,y,z

Lời giải:

\left| {x - z} \right| = \left| {(x - y) + (y - z)} \right| \le \left| {x - y} \right| + \left| {y - z} \right|

CLICK NGAY vào nút TẢI VỀ dưới đây để download Giải sách bài tập Toán lớp 10 tập 1 trang 106 file word, pdf hoàn toàn miễn phí.

Đánh giá bài viết
5.0
1 lượt đánh giá
CÔNG TY CỔ PHẦN TRUYỀN THÔNG HDC VIỆT NAM
Tầng 3, toà nhà S3, Vinhomes Skylake, đường Phạm Hùng, quận Nam Từ Liêm, Hà Nội
Liên hệ quảng cáo: tailieucom123@gmail.com
Copyright © 2020 Tailieu.com
DMCA.com Protection Status