Giải SBT Toán 10 trang 117, 118 tập 1 bài: Bất phương trình bậc nhất hai ẩn

Giải sách bài tập Toán 10 tập 1 bài 4 chương 4: Bất phương trình bậc nhất hai ẩn được giải đáp chi tiết và rõ ràng nhất, giúp cho các bạn học sinh có thể tham khảo và chuẩn bị tốt nhất cho bài học sắp tới nhé.

Giải bài 37 trang 117 SBT Toán lớp 10 tập 1

Biểu diễn hình học tập nghiệm của các bất phương trình sau:

a) 3 + 2y > 0;

b) 2x - 1 < 0;

c) x - 5y < 2;

d) 2x + y > 1;

e) −3x+y+2≤0;

f) 2x−3y+5≥0

Lời giải:

a) Điểm O(0;0) có tọa độ thỏa mãn bất phương trình, do đó miền nghiệm là nửa mặt phẳng bờ 3 + 2y = 0 chứa O (bỏ bờ).

b) Miền nghiệm là nửa mặt phẳng bờ 2x – 1 = 0 chứa O (bỏ bờ).

Giải SBT Toán lớp 10 tập 1 bài 38 trang 118

Biểu diễn hình học tập nghiệm của các hệ bất phương trình sau:

a) 

b) 

Lời giải:

a) 

(Vô nghiệm)

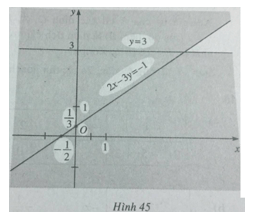
b) Miền nghiệm là phần mặt phẳng không bị tô đen (không kể bờ). (h.45).

Giải bài 39 trang 118 sách bài tập Toán lớp 10 tập 1

Một hộ nông dân trồng đậu và cà trên diện tích 8a. Nếu trồng đậu thì cần 20 công và thu 3 000 000 đồng trên một a, nếu trồng cà thì cần 30 công và thu 40 000 000 đồng trên một a. Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được nhiều tiền nhất khi tổng số công không quá 180?

Lời giải:

Gọi x là diện tích trồng đậu, y là diện tích trồng cà, (đơn vị a = 100 m²), điều kiện x≥0,y≥0, ta có x+y≤8

Số công cần dùng là 20x+30y≤180 hay 20+3y≤18

Số tiền thu được là

F=3000000x+4000000y (đồng)

Hay F = 3x + 4y (đồng)

Ta cần tìm x, y thỏa mãn hệ bất phương trình

Sao cho F = 3x + 4y đạt giá trị lớn nhất.

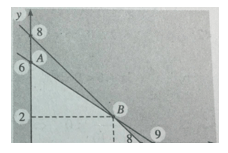
Biểu diễn tập nghiệm của (H) ta được miền tứ giác OABC với A(0;6), B(6;2), C(8;0) và O(0;0) (h.46).

Xét giá trị của F tại các đỉnh O, A, B, C và so sánh ta suy ra x = 6, y = 2 (tọa độ điểm B) là diện tích cần trồng mỗi loại để thu được nhiều tiền nhất là F = 26 (triệu đồng).

Đáp số: Trồng 6a đậu, 2a cà, thu hoạch 26 000 000 đồng.

CLICK NGAY vào nút TẢI VỀ dưới đây để download Giải sách bài tập Toán lớp 10 tập 1 trang 117, 118 file word, pdf hoàn toàn miễn phí.