Giải SBT Toán 10 trang 214, 215, 216, 217, 218 tập 1: Bài tập ôn tập cuối năm

Giải sách bài tập Toán 10 tập 1 bài: Bài tập ôn tập cuối năm được giải đáp chi tiết và rõ ràng nhất, giúp cho các bạn học sinh có thể tham khảo và chuẩn bị tốt nhất cho bài học sắp tới nhé.

Giải bài 1 SBT Toán lớp 10 tập 1 trang 214

Xác định parabol 

 trong mỗi trường hợp sau

a) Parabol nhận trục tung làm trục đối xứng và cắt đường thẳng 

 tại các điểm có hoành độ là -1 và 

b) Parabol đi qua gốc tọa độ và có đỉnh là điểm (1;2).

c) Parabol đi qua hai điểm A(-1; 2), B(2; 3) và có trục đối xứng là đường thẳng x = 1.

Lời giải:

a) Vì đồ thị nhận trục tung làm trục đối xứng cho nên hàm số 

 là hàm số chẵn, do đó

Suy ra b = 0. Ta còn phải xác định a và c.

Vì parabol cắt đường thẳng 

 tại các điểm có hoành độ -1 và  nên nó đi qua các điểm

 và 

Ta có hệ phương trình

Giải hệ phương trình trên ta được 

Parabol phải tìm là 

b) Vì parabol đi qua (0;0) nên y(0) = c = 0.

Do parabol có đỉnh là (1 ; 2) nên

Giải hệ phương trình trên ta được a = -2, b = 4.

Parabol phải tìm là 

c) 

Giải Toán lớp 10 SBT tập 1 bài 2 trang 214

Tìm các giá trị của k sao cho phương trình

có các nghiệm bằng nhau.

Lời giải:

Phương trình 

 có các nghiệm bằng nhau

⇔Δ=(k+4)2−4(k−1)(k+7)=0

⇔−3k2−16k+44=0

Giải bài 3 trang 214 SBT Toán lớp 10 tập 1

Với những giá trị nào của a, hiệu giữa hai nghiệm của phương trình

bằng tích của chúng?

Lời giải:

Ta có: 

 nên phương trình đã cho có nghiệm

Xét 

Hay 

Đáp số: a = 2

Giải SBT Toán lớp 10 tập 1 bài 4 trang 214

Hãy xác định k để hiệu giữa các nghiệm của phương trình 

 bằng 1.

Lời giải:

Cần có: 

Xét 

Suy ra 

Do đó

Đáp số: 

Giải sách bài tập Toán 10 tập 1 bài 5 trang 214

Tìm các giá trị của a sao cho tổng các nghiệm của phương trình

bằng tổng bình phương các nghiệm đó.

Lời giải:

Vì 

 nên phương trình luôn có nghiệm.

Ta có: 

Suy ra: 

Giải phương trình trên ta được 

Đáp số: 

Giải bài 6 SBT Toán lớp 10 tập 1 trang 214

Không giải phương trình

hãy tính tổng lập phương các nghiệm của nó.

Lời giải:

=(x₁+x₂)[(x₁+x₂)²−3x₁x₂]

Giải SBT Toán 10 tập 1 bài 7 trang 215

Tính 

, trong đó  và  là các nghiệm của phương trình bậc hai 

Lời giải:

Ta có:

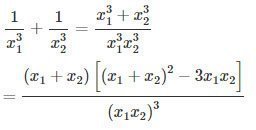
Giải Toán lớp 10 SBT tập 1 bài 8 trang 215

Tìm giá trị của a sao cho phương trình

có hai nghiệm dương phân biệt và đều lớn hơn 3.

Lời giải:

Phải có

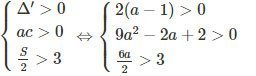
Giải hệ bất phương trình trên ta được a > 1.

Giải bài 9 SBT Toán lớp 10 tập 1 trang 215

Tìm các giá trị nguyên của k sao cho phương trình 

 vô nghiệm

Lời giải:

Phương trình 

 vô nghiệm

Xét (2):

Đặt 

Vậy: 

, mà k nguyên 

Từ (1) và (3) 

Giải Toán lớp 10 SBT tập 1 bài 10 trang 215

Cho phương trình bậc hai

Kí hiệu S là tổng, P là tích các nghiệm (nếu có) của phương trình trên.

a) Với giá trị nào của a, phương trình (E) có nghiệm?

b) Biện luận dấu của S và P. Từ đó suy ra dấu các nghiệm của (E).

c)Tìm hệ thức giữa S và P độc lập đối với a.

d) Với những giá trị nào của a, các nghiệm 

 của (E) thỏa mãn hệ thức ? Tìm các nghiệm  trong mỗi trường hợp đó.

Lời giải:

a) Phải có:

b) Ta có:

 khi đó 

 khi đó  cùng dấu.

Mặt khác 

Suy ra:

Với 

 thì hai nghiệm của phương trình (E) đều dương;

Với 

 thì hai nghiệm của phương trình (E) đều âm;

c) Từ 

 suy ra 

Do đó: 

d) 

Suy ra:

Với a = - 1 ta có: 

Với 

 ta có: 

Với 

 ta có: 

Giải bài 11 trang 215 SBT Toán lớp 10 tập 1

Giải và biện luận các hệ phương trình sau

a) 

b) 

Lời giải:

a) Với 

 hệ phương trình (1) có nghiệm 

Với 

 hệ phương trình (1) vô nghiệm.

b) Nếu 

 thì thì x = 0, y = a;

Nếu a = -1 thì x = t + 1, y = 1 

Nếu a = 1 thì (x = t,y = 1 - t 

Giải SBT Toán lớp 10 tập 1 bài 12 trang 215

Giải phương trình sau

a) 

b) 

Lời giải:

a) Hệ phương trình (3) tương đương với

Từ đó nếu 

 thì hệ có nghiệm

Ta xét:

Với m = -7 hệ phương trình (3) trở thành

Vì 

 nên hệ phương trình (3a) có vô số nghiệm.

Với m = 8 ta có hệ

Vì 

 cho nên hệ phương trình (3b) vô nghiệm.

Trả lời: m = -7.

b) Hệ phương trình (4) tương đương với

Tương tự câu a) ta xét trường hợp 

Với m = 3 ta có hệ phương trình

Rõ ràng hệ phương trình (4a) có vô số nghiệm.

Với m = -3 hệ phương trình (4) trở thành

Vì 

 cho nên hệ phương trình (4b) vô nghiệm.

Trả lời: m = 3.

Giải sách bài tập Toán 10 tập 1 bài 13 trang 215

Giải các hệ phương trình sau

a) 

b) 

Lời giải:

a) 

Đặt u = x + y ta được 

Giải ra ta được 

Với u = 3 ta có hệ phương trình

Với u = -4 ta được hệ phương trình

 (vô nghiệm)

Đáp số: (1; 2) và (2; 1).

b) Đặt

 ta được hệ phương trình

hay

Giải hệ phương trình trên ta được

u = 5, v = 2

hoặc u = 4, v = 1

Vậy

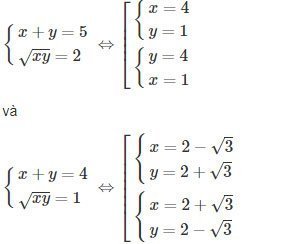
Đáp số: Hệ phương trình đã cho có bốn nghiệm là

Giải bài 14 SBT Toán lớp 10 tập 1 trang 216

Giải các hệ phương trình sau

Lời giải:

a)

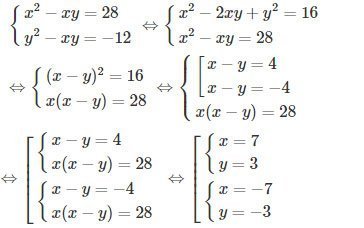
b)

Đặt 

ta có hệ phương trình đã cho tương đương với hệ phương trình:

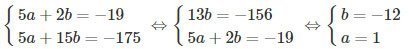
Vậy 

  là 2 nghiệm của phương trình

Vậy hệ phương trình có 2 nghiệm

và

Giải SBT Toán 10 tập 1 bài 15 trang 216

Giải các bất phương trình sau

a) 

b) 

c) 

e) 

g) 

Lời giải:

a) 

b) 

c) 

d) 

e) 

g) 

Giải Toán lớp 10 SBT tập 1 bài 16 trang 216

Trong mặt phẳng tọa độ Oxy, tìm tọa độ các đỉnh của tam giác ABC, biết tọa độ trung điểm của các cạnh BC, CA, AB lần lượt là M(1;2), N(3;-5), P(5; 7).

Lời giải:

Giả sử các đỉnh của tam giác có tọa độ lần lượt là

Theo công thức tọa độ trung điểm ta có:

và

Cộng từng vế các phương trình của hệ (I) ta được

Từ đó: 

Tương tự tìm được 

Vậy: 

Giải bài 17 SBT Toán lớp 10 tập 1 trang 216

Trong mặt phẳng tọa độ Oxy hãy tìm tọa độ các đỉnh M, N của hình vuông AMBN, biết tọa độ hai đỉnh A(1; 1) và B(3; 5).

Lời giải:

Giả sử M(x; y) là đỉnh của hình vuông AMBN.

Ta có:

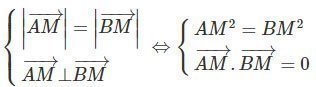
hoặc

Vậy M(4; 2), N(0; 4) hoặc M(0; 4), N(4; 2).

Giải sách bài tập Toán lớp 10 tập 1 bài 18 trang 216

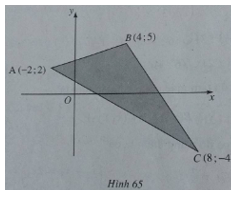
Biểu diễn hình học tập nghiệm của hệ bất phương trình

Lời giải:

(h.65) Tập nghiệm là miền tam giác ABC (kể cả biên).

Giải Toán lớp 10 SBT tập 1 bài 19 trang 217

Cho các số liệu thống kê ghi trong bảng sau

Thời gian giải xong một bài tập Toán của 44 học sinh lớp 10A, trường Trung học phổ thông K

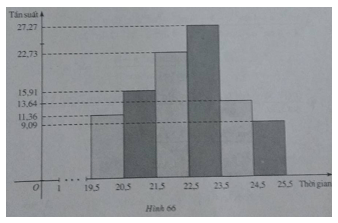
a) Lập bảng phân bố tần số và tần suất ghép lớp với các lớp như sau:

[19,5; 20,5); [20,5; 21,5); [21,5; 22,5); [22,5; 23,5); [23,5; 24,5); [24,5; 25,5].

b) Dựa vào bảng phân bố tần suất ghép lớp đã lập hãy nêu nhận xét về thời gian làm một bài tập của 44 học sinh kể trên.

c) Hãy tính số trung bình cộng 

, phương sai s²_x và độ lệch chuẩn s_x của các số liệu thống kê đã cho.

d) Giải sử rằng, cũng khảo sát thời gian giải xong một bài tập Toán của học sinh ở các lớp 10B, 10C của trường K, rồi tính các số trung bình cộng, phương sai và độ lệch chuẩn của các số liệu thống kê ở từng lớp, ta thu được kết quả sau:

Ở lớp 10B có 

=20 phút, s²_y=1, s_y=1 phút

Ở lớp 10C có 

=22 phút, s²_z=1, s_z=1phút

Hãy so sánh thời gian giải xong một bài tập Toán của học sinh ở ba lớp 10A, 10B, 10C đã cho.

e) Vẽ biểu đồ tần suất hình cột mô tả bảng phân bố tần suất ghép lớp đã lập được.

Lời giải:

a) Thời gian giải xong một bài tập toán của 44 học sinh lớp 10A, trường Trung học phổ thông K

b) Nhận xét:

Trong 44 học sinh đã được khảo sát ta thấy:

Chiểm tỉ lệ thấp nhất (9,09%) là những học sinh có thời gian giải xong một bài tập toán từ 24,5 phút đến 25,5 phút.

Chiểm tỉ lệ cao nhất (27,27%) là những học sinh có thời gian giải xong một bài tập toán từ 22,5 phút đến dưới 23,5 phút.

Đa số (79,55%) là những học sinh có thời gian giải xong bài tập toán đó từ 20,5 phút đến dưới 24,5 phút.

Đa số (79,55%) là những học sinh có thời gian giải xong bài tập toán đó từ 20,5 phút đến dưới 24,5 phút.

c) Sử dụng bảng phân bố tần số ghép lớp đã lập, ta tính được 

 phút,  phút

d) Ta có 

 phút >20 phút  và  nên thời gian giải xong bài tập toán đó của các học sinh lớp 10C là đồng đều hơn các học sinh lớp 10A.

e) Biểu đồ tần suất hình cột về thời gian (phút) giải xong một bài tập toán của 44 học sinh lớp 10A, trường Trung học phổ thông K (h.66)

Giải bài 20 trang 217 SBT Toán lớp 10 tập 1

Chứng minh rằng

a) 

b) 

c) 

d) 

e) 

Lời giải:

a) Vì 

 cho nên

b)

c)

Giải SBT Toán lớp 10 tập 1 bài 21 trang 218

Rút gọn

a) 

b) 

c) 

Lời giải:

a)

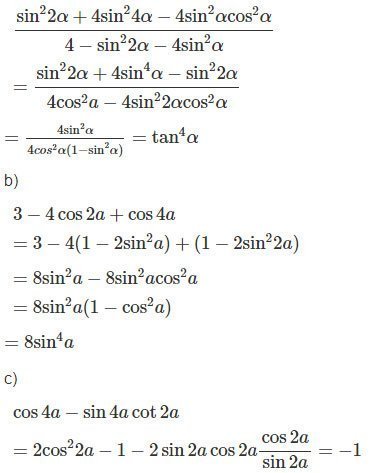
d) 

Giải sách bài tập Toán 10 tập 1 bài 22 trang 218

Không dùng bảng số và máy tính, hãy tính

a) 

 và 

b) 

c) 

d) 

Lời giải:

a) 

b)

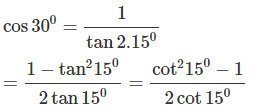
Đặt 

 và chú ý rằng  ta có

Giải phương trình trên ta được 

 (nghiệm  loại vì . Do đó

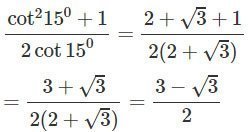
c) Ta có:

d) Hướng dẫn: Nhân thêm 

Đáp số: 

Giải bài 23 SBT Toán lớp 10 tập 1 trang 218

Chứng minh rằng

a) 

b) 

c) 

d) 

Lời giải:

a)

b)

c)

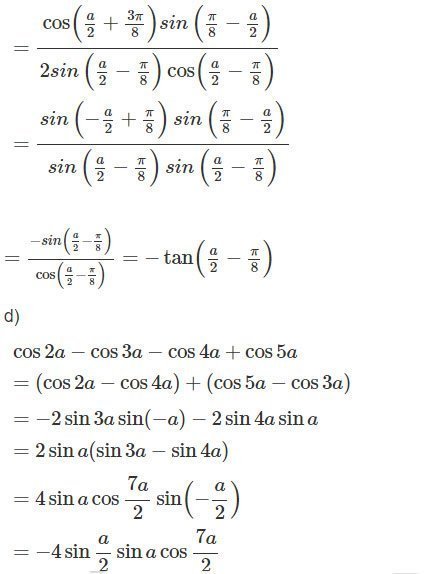
Giải SBT Toán 10 tập 1 bài 24 trang 218

Rút gọn

a) 

b) 

c) 

d) 

Lời giải:

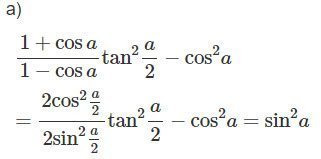
b)

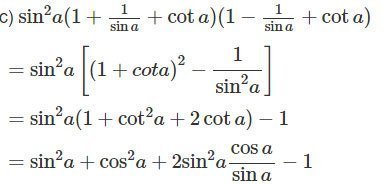
d)

CLICK NGAY vào nút TẢI VỀ dưới đây để download Giải sách bài tập Toán lớp 10 tập 1 trang 214, 215, 216, 217, 218 file word, pdf hoàn toàn miễn phí.